DS博客作业02--栈和队列

| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业02--栈和队列 |
| 这个作业的目标 | 学习栈和队列的结构设计及运算操作 |

0.PTA得分截图

1.本周学习总结

1.1 栈

• 顺序栈的结构、操作函数

主要操作函数如下：

InitStack(SqStack &s) 参数：顺序栈s 功能：初始化  时间复杂度O(1)
Push(SqStack &s,SElemType e) 参数：顺序栈s,元素e 功能：将e入栈 时间复杂度:O(1)
Pop(SqStack &s,SElemType &e) 参数：顺序栈s,元素e 功能：出栈,e接收出栈元素值 时间复杂度O(1)
GetTop(SqStack s,SElemType &e) 参数：顺序栈s,元素e 功能：得到栈顶元素 时间复杂度O(1)

• 链栈的结构、操作函数

主要包含以下几个函数：

InitStack(LinkStack &S) 参数：链栈S 功能：初始化  时间复杂度O(1)
Push(LinkStack &S,SElemType e) 参数：链栈S,元素e 功能：将e入栈 时间复杂度:O(1)
Pop(LinkStack &S,SElemType &e) 参数：链栈S,元素e 功能：栈顶出栈,e接收出栈元素值 时间复杂度O(1)
GetTop(LinkStack &S,SElemType &e) 参数：链栈S,元素e 功能：得到栈顶元素 时间复杂度O(1)

1.2 栈的应用

一、 栈的应用

• 递归

在高级语言中，调用自己和其他函数并没有本质的不同。我们把一个直接调用自己或通过一系列的调用语句间接地调用自己的函数，称做递归函数。
函数自己调用自己，听起来有些难以理解，不过可以不要把一个递归函数中调用自己的函数看做是在调用自己，而就当它是在调用另一个函数。只不过，这个函数和自己长得一样而已。当然，写递归程序最怕的就是陷入永不结束的无穷递归中，所以，每个递归都需要一个退出递归的条件。递归使用的是选择结构。递归能使程序的结构更清晰、更简洁、更容易让人理解，从而减少读懂代码的时间。但是大量的递归调用会建立函数的副本，会消耗大量的时间和内存。那么我们讲了那么多递归的内容，和栈有什么关系呢？程序设计基础阶段我们已经了解了递归是如何执行它的前行和退回的。递归过程退回的顺序是它前行顺序的逆序。显然这符合栈的存储方式。简单的说，就是在前行阶段，对于每一层递归，函数的局部变量、参数值以及返回地址都被压如栈中。在退回阶段，位于栈顶的局部变量、参数值和返回地址被弹出，用于返回调用层次中执行代码的其余部分，也就是恢复了调用的状态。当然，对于现在的高级语言，这样的递归问题是不需要用户来管理这个栈的，一切都由系统代劳就可以了。

• 进制转换

 在计算机中存储的数据都是二进制，所以往往需要把十进制数据转换成二进制，转换的过程实际就是除2取余数，这其中我们可以看到最先求得余数实际是个位数，书写一个数据的时候都是先书写高位的数据，而后依次到个位。这正好和栈后进先出的特性吻合，因此可以使用栈来存储。

例如：十进制的25转换成2进制

  25  25/2 25%2      n    0==n/2    y=n%2

  25  12     1

  12   6     0

  6    3     0

  3    1     1

  1    0     1
根据最后得到的是高位，先除余得到的是个位，最后得到的二进制值是：11001

• 括号匹配

判断一个表达式的”(“和”）”是否匹配，思路是这样的：遇到”（“则入栈，遇到”）”则从栈顶弹出”（“与之配成一对，当整个表达式扫描完毕时：

（1） 若栈内为空，则说明（与）是匹配的。

（2） 若表达式扫描完毕，栈内仍有（则说明左括号是多的。

（3） 若当）被扫描到，栈里却没有（能弹出了，说明）多，表达式中）也是多的。

• 表达式求值

算法思想：

（1） 首先置操作数栈OPND为空栈，表达式的起始符#为运算符栈OPTR的栈底元素；

（2） 依次读入表达式中的每个字符

若运算符是‘#’或栈顶是‘#’，结束计算，返回OPND栈顶值。

  if（是操作数） → 则PUSH（ OPND，操作数）；

  if（是运算符） → 则与OPTR栈顶元素进行比较，按优先级进行操作；

优先级操作细则如下：

① if栈顶元素<输入算符，则算符压入OPTR栈，并接收下一字符

② if栈顶元素=运算符但≠‘#’，则脱括号(弹出左括号)并收下一字；

③ if栈顶元素>运算符，则退栈、按栈顶计算，将结果压入OPND栈。

④ 且该未入栈的运算符要保留，继续与下一个栈顶元素比较！

表达式求值过程的描述：3*（7 – 2 ）

栈的表达式

1、逆波兰表达式简介

  假定给定一个只 包含 加、减、乘、除，和括号的算术表达式，你怎么编写程序计算出其结果。问题是：在表达式中，括号，以及括号的多层嵌套 的使用，运算符的优先级不同等因素，使得一个算术表达式在计算时，运算顺序往往因表达式的内容而定，不具规律性。 这样很难编写出统一的计算指令。
  使用逆波兰算法可以轻松解决。他的核心思想是将普通的中缀表达式转换为后缀表达式。

  转换为后缀表达式的好处是：

* 去除原来表达式中的括号，因为括号只指示运算顺序，不是完成计算必须的元素。

* 使得运算顺序有规律可寻，计算机能编写出代码完成计算。虽然后缀表达式不利于人阅读，但利于计算机处理。

2、将中缀表达式转换成后缀式（逆波兰表达式

1. 从左到右读进中序表达式的每个字符。

2. 如果读到的字符为操作数，则直接输出到后缀表达式中。

3. 如果遇到“)”，则弹出栈内的运算符，直到弹出到一个“(”,两者相互抵消。

4. “(”的优先级在栈内比任何运算符都小，任何运算符都可以压过它，不过在栈外却是优先级最高者。

5. 当运算符准备进入栈内时，必须和栈顶的运算符比较，如果外面的运算符优先级高于栈顶的运算符的优先级，则压栈；如果优先级低于或等于栈顶的运算符的优先级，则弹栈。直到栈顶的运算符的优先级低于外面的运算符优先级或者栈为空时，再把外面的运算符压栈。

6. 中缀表达式读完后，如果运算符栈不为空，则将其内的运算符逐一弹出，输出到后缀表达式中。


//比较lhs的优先级是否不高于rhs，rhs表示栈顶的符号
bool priority(const char &lhs, const char &rhs)
{
    if (rhs == '(')//左括号在栈外优先级最高
        return false;
    if (lhs == '+' || lhs == '-')
        return true;
    if ((lhs == '*' || lhs == '/') && (rhs == '*' || rhs == '/'))
        return true;
    return false;
}
//将中缀表达式转换成后缀式（逆波兰表达式）
string exchange(const string &str)
{
    vector<char> vec;
    string res;
    stack<char> st;//操作符堆栈
    for (int i = 0; i < str.size(); ++i)
    {
        if (isdigit(str[i]))//如果是数字，直接输出到后序表达式中
        {
            vec.push_back(str[i]);
        }
        else//如果是符号,需要与栈顶的元素进行比较
        {
            if (st.empty() || str[i] == '(')//小括号在栈外优先级最高，直接压栈
                st.push(str[i]);
            else
            {
                if (str[i] == ')')//遇到右括号，则弹栈，直到遇到左括号，两者相互抵消
                {
                    while (!st.empty() && st.top() != '(')
                    {
                        vec.push_back(st.top());
                        st.pop();
                    }
                    st.pop();
                }
                else//遇到的是其他操作符
                {
                    if (priority(str[i], st.top()))//优先级比栈顶元素低
                    {
                        while (!st.empty())
                        {
                            vec.push_back(st.top());
                            st.pop();
                        }
                        st.push(str[i]);
                    }
                    else//优先级比栈顶元素高，压栈
                    {
                        st.push(str[i]);
                    }
                }
            }
        }
    }
    while (!st.empty())//如果堆栈不为空，则将其中的元素全部弹出
    {
        vec.push_back(st.top());
        st.pop();
    }
    for (auto v : vec)
        res += v;
    return res;
}

3、后缀表达式求值

后缀表达式具有和前缀表达式类似的好处，没有优先级的问题。

1. 直接读取表达式，如果遇到数字就压栈。

2. 如果遇到运算符，就弹出两个数进行运算，随后再将运算结果压栈。


//定义四则运算
int operate(int first, int second, char op)
{
    int res = 0;
    switch (op)
    {
        case '+':
            res = first + second;
            break;
        case '-':
            res = first - second;
            break;
        case '*':
            res = first*second;
            break;
        case '/':
            res = first / second;
            break;
        default:
            break;
    }
    return res;
}

int calculate(string input)
{
    stack<int> st;//操作数堆栈
    for (auto &s : input)
    {
        if (isdigit(s))//如果是数字就压栈
        {
            st.push(s - '0');
        }
        else//遇到字符就弹出两个操作数进行运算
        {
            int a = st.top();
            st.pop();
            int b = st.top();
            st.pop();
            st.push(operate(b, a, s));
        }
    }
    return st.empty() ? 0 : st.top();//最后的结果为栈顶元素
}

1.3 队列

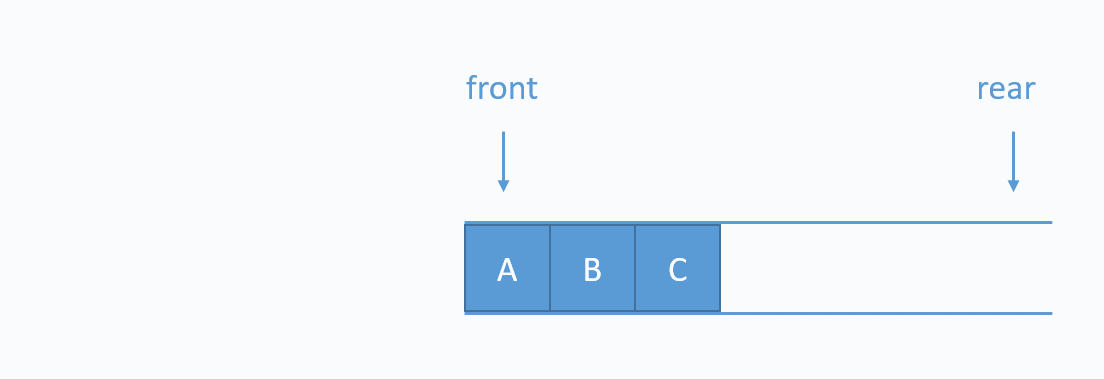
1.3.1 队列的数据类型

队列当中没有位置的概念，只要求保证先进先出即可。

1.3.2 队列的数据操作

1.3.2 队列的实现（主要基于线性表的技术）

1.3.2.1 基于链表的实现代码（由于队列实质上是线性表约束下的结构，所以只需要在线性表的基础上修改）

//链表的基础上实现队列

class Lnote():
    def __init__(self,ele=None,next_=None):
        self._element=ele
        self._next = next_
 
class Llist():
    def __init__(self):
        self._head = None
    def preappend(self,ele):  # 于表头添加元素
        self._head = Lnote(ele,self._head)
 
    def out_me(self):   # 于表尾弹出元素
        p = self._head
        if p == None:
            print('队列里无元素')
        elif p._next == None:
            print(p._element)
            self._head=None
        else:
            while p._next is not None:
                p0=p
                p = p._next
            print(p._element)
            p0._next = None    # 记住一定是改指针p的next而非直接给节点赋值为None

1.3.2.2 基于顺序表的固定容量的队列实现代码

这里需要说明的是：

• 利用list为基础构造的队列，固定循环长度是必要的。有两种循环的方法，①指针到了最末端，指定回到0②用p%len.也可以优雅的循环指针。这里采取了前者。
• 在队头指针与队尾指针相等时，队列为空，当队尾+1刚好等于队头时，队列为满。
• 用指针为引索，给定义好的列表赋值。

1.3.2.3 基于list的无限容量队列的实现代码

由于list的自动扩容机制和队列的扩容机制不一致，所以必须设计队列独有的扩容机制
会定义新的异常类
考虑到SQueue类里面必须有的变量: _head(队首位置),_elements(元素),_nums（元素个数），_len(list的长度)。 
数据不变式的概念：类里面的各种属性之间的相互平衡，每个属性的变化所牵涉到的另一个属性的变化规则。只有遵从这里面的关系，才能保证类在操作过程中不会出现问题。满足数据不变式要做到两点，① 初始状态的属性满足 ② 类的操作之后不会破坏。

2.PTA实验作业

2.1 符号配对

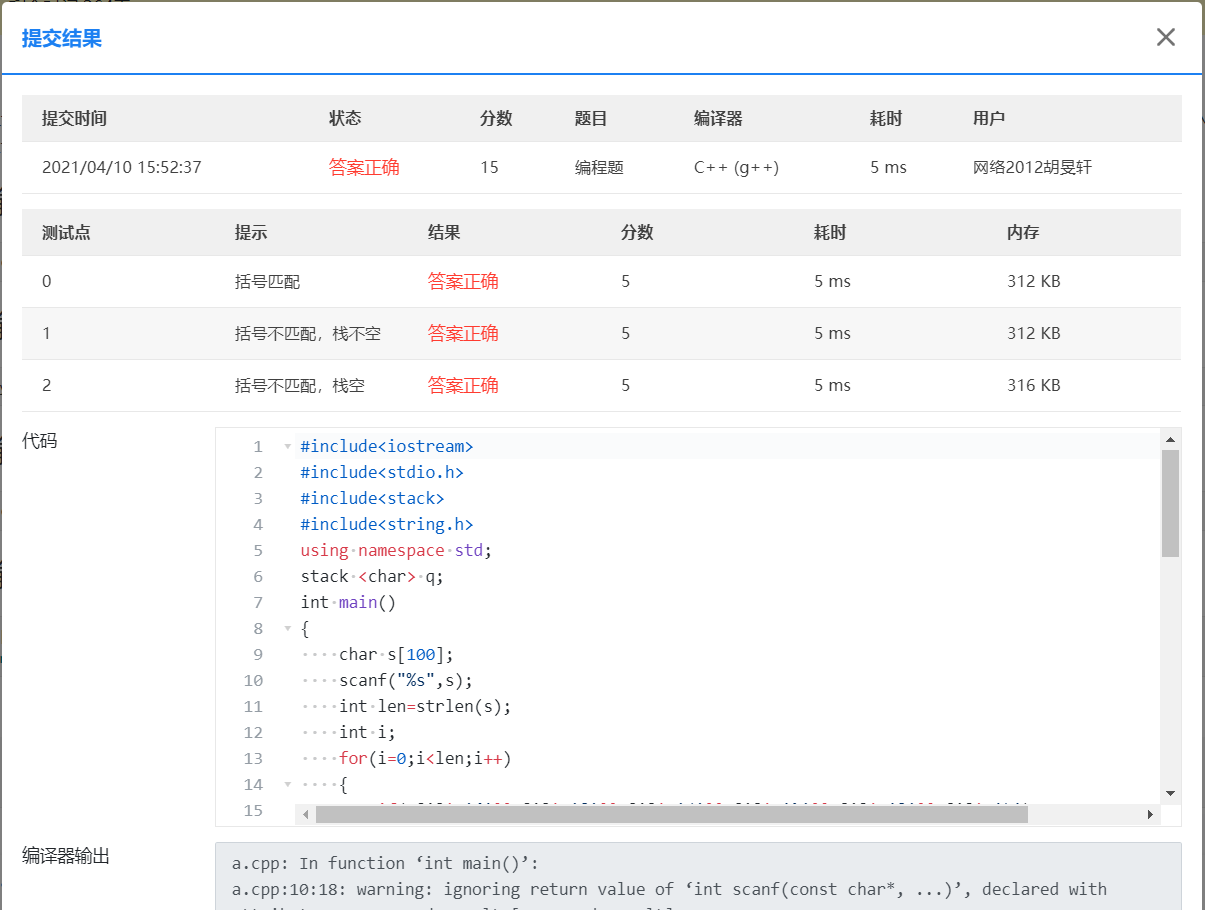
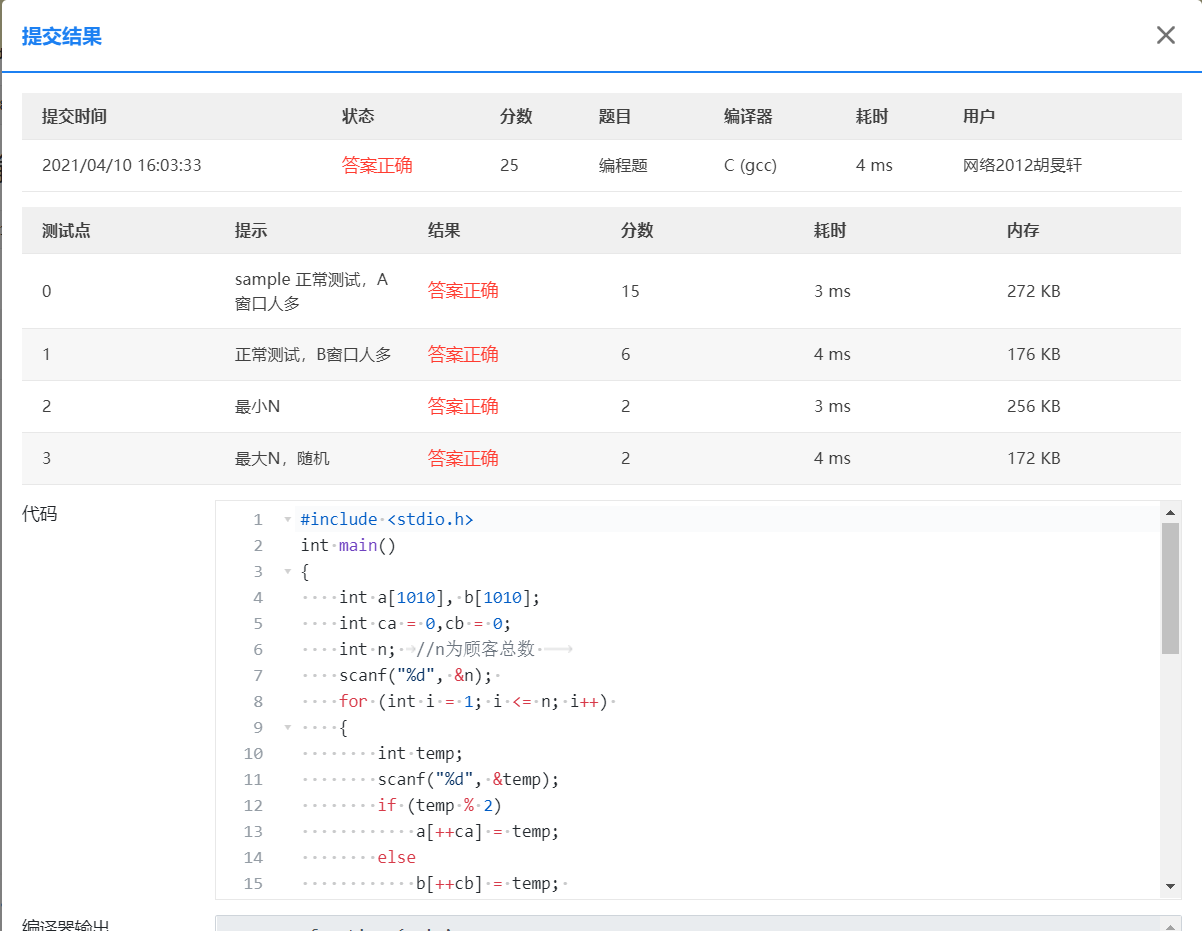
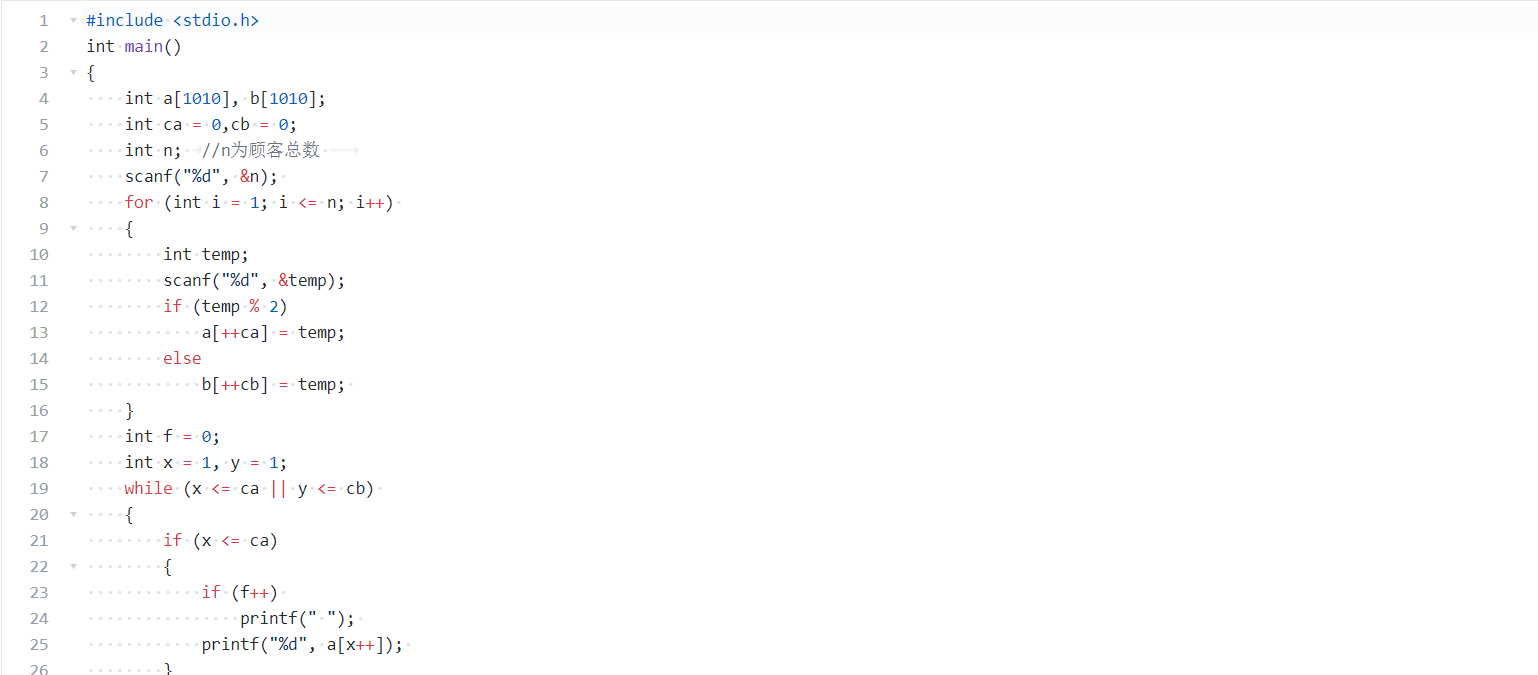
2.2 银行业务队列简单模拟