洛谷P4296 [AHOI2007] 密码箱——题解

题目传送：https://www.luogu.com.cn/problem/P4296

跟扩展欧几里得和中国剩余定理并没有什么关系。。

没有几个题解的明确、简便地说明复杂度，本文会简单说明一下。注：本文计算复杂度时的误差极大，只求规模与实际复杂度差不多。

 

 

 

 

 

 

 

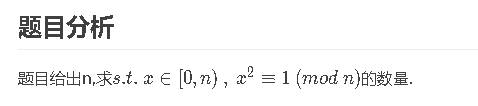
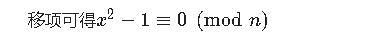
 　　即n|(x-1)(x+1)，可看做(x-1)提供了一部分n的因数，(x+1)提供了另一部分n的因数，即 存在整数a,b，a|x-1,b|x+1，a*b=n。

　　那么对于一个x若同时满足a|x-1,b|x+1,a*b=n  ，则x就是一个可行的答案。由于满足a*b=n的无序数对最多有sqrt（n）个，可以考虑枚举所有a,b，去找所有能满足a|x-1,b|x+1的x以求得答案。

　　不妨设a<b，又有a*b=n，则有1<=a<=sqrt(n)<=b<=n，则可以从1到sqrt（n）枚举可能的a，而b=n/a。但上文“a|x-1,b|x+1”中a不一定<=b，故对于当前枚举的a和b，要找能满足（a|x-1＆＆b|x+1）||（a|x+1＆＆b|x-1）的x。

　　x满足a|x-1＆＆b|x+1，即x-1=ka,x+1=k'b。按顺序的思路，可令x=ka+1（即枚举k），判断(x+1)%b。但这样的话，k的规模为n/a，而a<sqrt(n)，总复杂度上限约为 n/1（如果a从1开始枚举的话）+n/2+。。。+n/sqrt(n)约为n ln sqrt（n）可能比O(n)暴力都慢了就离谱了（实际上这个水题暴力都能拿100分）。

　　　　一般人可能到这就放弃这个思路了，但大佬发现枚举顺序不是唯一的，还可以令x=k‘b-1（即枚举k'），判断(x-1)%a。因为b>=sqrt(n)，故k’的规模为n/b<=sqrt(n)，则此时最坏的总复杂度上限级别也达不到1（a从1开始枚举的话，b一开始就等于n了）+2+。。。+sqrt（n）约等于n（等差数列求和）。实际上因数个数与数据规模的关系有下图： 

 

　　　　按照这种趋势的话，就算是n<=2e9，有最多因数的数的因数个数估计也不会超过3000吧，那也比sqrt（n=2e9）（约为44721.359549995793928183473374626）小多了，即上文的数列的项数只有3000项不到,用等差数列求和估计出的复杂度上限在n的值在2e9附近时也只有1500sqrt（n）约为6e7。实际上这个级别的复杂度上限是很难达到的，就算再加个log来维护答案的有序、唯一性问题也不大。（更何况本题最极限的数据n=2e9的因数只有区区110个，一点也不极限）

 本人用的数组存储答案，最后sort一遍，输出时防重处理。

ac代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>

#define ll long long
#define ull unsigned long long
#define min(a,b) ((a)>(b)?(b):(a))
#define max(a,b) ((a)>(b)>(a):(b))
#define swap(a,b) ((a)^=(b),(b)^=(a),(a)^=(b))

using namespace std;

const int N=2e9;

int n,ans[2000000],cnt;//赌一手答案不会超过2000000个。不想赌的话可用别的数据结构或vector，这里懒得改了。 

inline int read()//int N
{
    int x=0;
    bool f=0; 
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar(),f|=ch=='-';
    while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return f?-x:x;
} 
 
int main()
{
    n=read();
    if(n==1)//唯一无解的情况 
    {
        cout<<"None";
        return 0;
    }
    ans[++cnt]=1;//x以后大于1，即无x-1=0的情况了 
//    （x=1的情况可能会判断多次，导致去重前的答案序列会有很多1，不如在枚举前就处理一下）
    long long b,x;
    for(long long a=1;a*a<=n;++a)
        if(n%a==0)
        {
            b=n/a;
            for(x=b+1;x<n;x+=b)
            {
                if((x+1)%a==0)
                    ans[++cnt]=x;
            }
            x=b-1;
            if(x==1)
                x+=b;
            for(;x<n;x+=b)//有位大佬说的好，4e9在int范围外。所以涉及计算的量都要开long long 
            {
                if((x-1)%a==0)
                    ans[++cnt]=x;
            }
        }        
    sort(ans+1,ans+cnt+1);
    int las=0;
    for(int i=1;i<=cnt;++i)
        if(ans[i]!=las)
        {
            las=ans[i];
            printf("%d\n",ans[i]);
        }
    return 0;
}

 

 

图片引用：

https://www.luogu.com.cn/blog/SuperTNT/solution-p4296

https://www.luogu.com.cn/blog/lemir3/solution-p4296

https://www.cnblogs.com/InductiveSorting-QYF/p/15168013.html