二叉查找树
2020.7.25 update:优化了树中已有点找前驱后继的方法(详见“删除”);普通情况找前驱后继的正确性。
一、总述:
二叉查找树,是指根的左子树都比根小,右子树都比根大,且左右子树也是二叉查找树的二叉树,如图: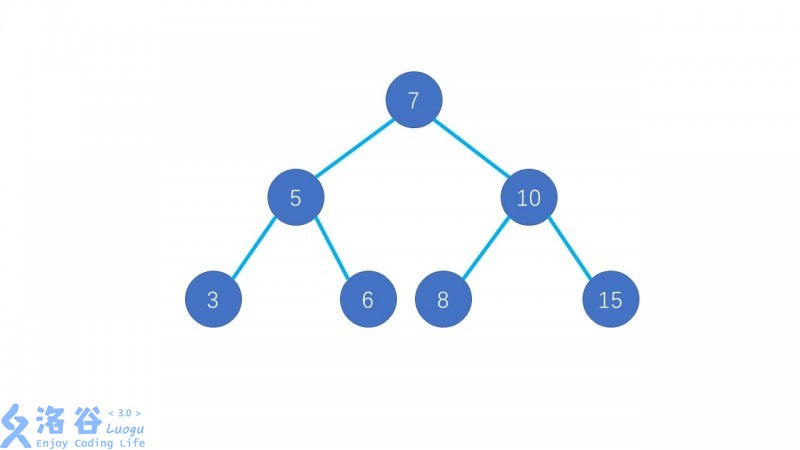
可见,每个节点的左子树都比这个节点小、右子树都比这个节点大,若从左向右依次看每个节点,则是从小到大的。
作用:随机数据下快速查找,支持修改。
二、基本操作:
1、查找一个数x是否存在
在二叉查找树中查询x是否存在,先从树的根开始看,若根对应的值y:
等于x:若个数不小于1,则查找成功,返回相应查找成功信息,否则失败,返回相应查找失败信息。
大于x:递归看左子树
小于x:递归看右子树
一直递归到找到x(即查找成功)或要看的子树为空(即x在二叉查找树中不存在,这时返回相应查找失败信息)后,操作就完成了。

//u表示当前节点的编号, //v是当前要插入的数,val表示的是节点的键值,rank表示排名, //size表示以当前节点的为根的子树的大小,示例维护额外信息 //cnt表示当前节点代表的数(键值)的个数 //ls是左儿子,rs是右儿子 //x为结构体数组,记录每个节点的信息 //bnt为出现过的节点的总数(在增加的过程中给节点编号) //root为根节点编号 int find(int val,int u) { if(u==0) return 0; if(val==x[u].val) return u; if(val>x[u].val) return fin(val,x[u].rs); else return fin(val,x[u].ls); }
2、插入一个数x
向二叉查找树中插入一个数x,先与树的根所对应的值y进行比较,若y
等于x:让该节点的cnt个数标记加一,或什么都不做(视题目要求)
大于x:若有左儿子,递归看左子树;否则,建立他的左儿子,其键值为x
小于x:若有右儿子,递归看右子树;否则,建立他的右儿子,其键值为x
一些子树大小等信息也可在递归过程中沿路维护。

//u表示当前节点的编号, //v是当前要插入的数,val表示的是节点的键值,rank表示排名, //size表示以当前节点的为根的子树的大小,示例维护额外信息 //cnt表示当前节点代表的数(键值)的个数 //ls是左儿子,rs是右儿子 //x为结构体数组,记录每个节点的信息 //bnt为出现过的节点的总数(在增加的过程中给节点编号) void add(int u, int v) { x[u].size++; if (x[u].val == v) { x[u].cnt++; return; } if (x[u].val > v) { if (x[u].ls != 0) add(x[u].ls, v); else { bnt++; x[bnt].val = v; x[bnt].size = 1; x[bnt].cnt = 1; x[u].ls = bnt; } } else { if (x[u].rs != 0) add(x[u].rs, v); else { bnt++; x[bnt].val = v; x[bnt].size = 1; x[bnt].cnt = 1; x[u].rs = bnt; } } }
3、删除一个数x
一法:可以利用cnt标记,找到这个数后cnt--即可,如果为cnt=0,就表示此时已经没有这个数。
二法:不利用cnt标记,直接改变树的结构。
删除节点存在 3 种情况,几 乎所有类似博客都提到了这点。这 3 种情况分别如下:
- 没有左右子节点,可以直接删除
- 存在左节点或者右节点,删除后需要对子节点移动
- 同时存在左右子节点,不能简单的删除,但是可以通过和后继节点子树内的后继节点 交换后转换为前两种情况
(update)若求树中已有点的后继,可从该点右走一格后找向左走的尽头;已有点的前驱,可从该点左走一格后找向右走的尽头。即代码可更优。
没有左右子节点时,只需要删除该节点、该节点和父节点的关系(若有父节点)即可。
存在左节点或者右节点时,先让子节点与父节点儿子为自己的那一侧建立连接(若有父节点),删除自己即可。若自己即为根节点,注意标记儿子为新根。
同时存在左节点和右节点时,先找到这个节点u的后继节点v,即为其右子树的最小值所在节点,即其右子树最左的节点。将u的键值改为v的键值,将v删除。由于u的后继节点v一定没有左儿子,故删除v为前两种删除情况。

//u表示当前节点的编号, //v是当前要插入的数,val表示的是节点的键值,rank表示排名, //size表示以当前节点的为根的子树的大小,示例维护额外信息 //cnt表示当前节点代表的数(键值)的个数 //ls是左儿子,rs是右儿子 //x为结构体数组,记录每个节点的信息 //bnt为出现过的节点的总数(在增加的过程中给节点编号) //root为根节点编号 //f[]记录每个节点的父节点,可在插入时维护 int next; void delete(int u)//u可由查找操作得到 { if(x[u].ls==0&&x[u].rs==0&&f[u]) { if(x[f[u]].ls==u) x[f[u]].ls=0; else x[f[u]].rs=0; } if(x[u].ls&&x[u].rs) { GetNext(x[u].rs,x[u].val);//见后文代码 x[u].val=x[next].val; delete(next); } if(x[u].ls) { if(f[u]) { if(x[f[u]].ls==u) x[f[u]].ls=x[u].ls; else x[f[u]].rs=x[u].ls; f[x[u].ls]=f[u]; } else { root=x[u].ls; f[x[u].ls]=0; } } else { if(f[u]) { if(x[f[u]].ls==u) x[f[u]].ls=x[u].rs; else x[f[u]].rs=x[u].rs; f[x[u].rs]=f[u]; } else { root=x[u].rs; f[x[u].rs]=0; } } }
4、查找一个数x的前驱或后继
前驱:树中小于x的最大数;后继:树中大于x的最小数
找前驱:从根节点开始,如果当前节点键值大于等于x,递归它的左子树,反之递归它的右子树,直到子树为空。递归过程记录答案,最终的答案即为所求;若答案没有找到过,则无前驱。
找后继:从根节点开始,如果当前节点键值大于x,递归它的左子树,反之递归它的右子树,直到子树为空。递归过程记录答案,最终的答案即为所求;若答案没有找到过,则无后继。
(update)正确性:不断优化答案,排除了剩下全部的劣解、错解。

//u表示当前节点的编号, //v是当前要插入的数,val表示的是节点的键值,rank表示排名, //size表示以当前节点的为根的子树的大小,示例维护额外信息 //cnt表示当前节点代表的数(键值)的个数 //ls是左儿子,rs是右儿子 //x为结构体数组,记录每个节点的信息 //bnt为出现过的节点的总数(在增加的过程中给节点编号) int pre,next; void GetPre(int u, int val) { if (x[u].val >= val) //* { if (x[u].ls == 0) return; else GetPre(x[u].ls, val); } else { if (x[u].cnt != 0) //若有cnt标记,则要有判断 pre = x[u].val; if (x[u].rs == 0) return; else GetPre(x[u].rs, val); } } void GetNext(int u, int val) { if (x[u].val > val) //* { if (x[u].cnt != 0) next = x[u].val; if (x[u].ls == 0) return; else GetNext(x[u].ls, val); } else { if (x[u].rs == 0) return; else GetNext(x[u].rs, val); } }
5、查找第x小的数(按排名找值)
查找二叉查找树中第x小的数y,即有x-1个数比y小。这里size表示树的大小指的是树中包含所有数的个数,可能不等于节点数(若有cnt标记的话)。从整个树开始递归,设根u的左子树的size为lsize,若lsize:
加上u.cnt后仍小于x:递归根的右子树,问题转化为查找右子树中第(x-lsize-u.cnt)小的数;
大于等于x:递归根的左子树,问题转化为查找左子树中第x小的数;
都不满足:则根的键值为所求。
若没使用cnt标记,u.cnt即为1。

//u表示当前节点的编号, //v是当前要插入的数,val表示的是节点的键值,rank表示排名, //size表示以当前节点的为根的子树的大小,示例维护额外信息 //cnt表示当前节点代表的数(键值)的个数 //ls是左儿子,rs是右儿子 //x为结构体数组,记录每个节点的信息 //bnt为出现过的节点的总数(在增加的过程中给节点编号) int GetValByRank(int u, int rank) { if (u == 0) //树中数的个数还不足x个 return INF; if (x[x[u].ls].size >= rank) return GetValByRank(x[u].ls, rank); if (x[x[u].ls].size + x[u].cnt < rank) return GetValByRank(x[u].rs, rank - x[x[u].ls].size - x[u].cnt); return x[u].val; }
5、查找x的排名(按值找排名)
二叉查找树中x的排名(设这里是从小到大排),即小于x的数的个数+1。设一个统计变量tot=1(即它自己),从整个树开始递归,若根的键值:
等于x:lsize+tot即为所求
大于x:递归根的左子树,若为空,tot即为所求;
小于x:tot+=lsize+u.cnt,递归右子树,若为空,tot即为所求。

1 //u表示当前节点的编号, 2 //v是当前要插入的数,val表示的是节点的键值,rank表示排名, 3 //size表示以当前节点的为根的子树的大小,示例维护额外信息 4 //cnt表示当前节点代表的数(键值)的个数 5 //ls是左儿子,rs是右儿子 6 //x为结构体数组,记录每个节点的信息 7 //bnt为出现过的节点的总数(在增加的过程中给节点编号) 8 9 int tot=1; 10 11 void GetRankByVal(int u,int val) 12 { 13 return; 14 if(val==x[u].val) 15 { 16 tot+=x[x[u].ls].size; 17 return; 18 } 19 if(val<x[u].val) 20 GetRankByVal(x[u].ls,val); 21 tot+=x[x[u].ls].size+x[u].cnt; 22 GetRankByVal(x[u].rs,val); 23 }
后记:
当树被数据卡成一条链时,大多数操作的效率都会退化为O(n),这时就需要平衡树了。
参考资料:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号