浅析差分及其推广(树上差分与广义差分)
所谓差分,就是记录当前的元素与之前元素逻辑上的差距。
最基础的用法是差的差分数组:
记录当前位置的数与上一位置的数的差值。
即b[i]=a[i]-a[i-1] (b为差分数组,a为原数组)
通过对差分数组求前缀和,可以求出原数组,即:

甚至可以求出前缀和:

(s为原数组,sum为原数组的前缀和数组,b为差分数组)
可以O(1)优化区间加法:给原数组区间[l,r]的数都加上x,只要在b l处加x,b r+1 处减x。
有两种理解角度:
1、从差分定义出发,区间加x使区间左端点与它在原数组上一个数的差距加大了x、使区间右端点的后一个数与区间右端点的数的差距缩小了x,而没有改变区间中相邻2数的差距。
2、从差分数组的修改对原数组的影响入手:由于差分数组求前缀和得出原数组,当b l加x之后求前缀和,那么原数组自l及以后的数全部比b l加x之前多了x;同理当b r+1减x之后求前缀和,那么原数组自r+1及以后的数全部比b r+1减x之前少了x。总的一看,发现原数组l~r的部分就多了x,其余部分没有变化。
广义差分:差分维护的是相邻元素间的逻辑关系,从而使能从初始状态(a[0])通过差分数组表达的逻辑关系推出某个位置上a的值(从形式上看就是求前缀)。而这种差距不只限于减法的差,还有异或等等。不过一般这种关系应可交换(即对顺序的要求不严格)且对于运算来说有单位元(么元)(或一般化的话就是要能有互相抵消的方法)
树上差分:将差分搬到了树上。可以有两个差分方向:
1、记录当前节点与父节点的逻辑关系,查询时从上往下求前缀。(不常用,因为在每次路径修改时都要修改一下当前节点的所有子节点,时间、程序复杂度都很高,没有灵魂的差分(不能O(1)实现路径修改))
2、记录当前节点与它所有子节点总和的逻辑关系,查询时dfs求子树和(或是说以向上为正方向的求前缀)。(路径修改时只要修改一下路径起始点和lca(有时还有lca的父亲),有了灵魂的差分(可O(1)实现路径修改),很常用)
树上差分分为点差分和边差分,不论哪种差分,差分数组的意义都是当前节点与它儿子节点总和的差距(这里为当前点(或点上的边)被路径经过次数与它的儿子节点(或其上的边)被路径经过次数总和的差,每次新增一个路径,即要求实现路径修改时,起始点与儿子们的差会多一,路径中中间的点与儿子们的差不变。点差分时,lca会比儿子们少1,lca的父亲会比儿子们少1;边差分时,lca会比儿子们少二。用这些逻辑关系从叶子向上推时,若当前点的儿子们的值都是对的,那它也是对的。边界情况就是叶子结点,显然是它的值对的,故可通过回溯推出整个树的值。这样对差分概念的理解有深入了:差分的结构不知限于线性的数组)
(这里的基础讲解引用自大佬的博客)
前置知识:
需要知道的树的性质:
1、树上任意两个点的路径唯一.
2、任何子节点的父亲节点唯一.(可以认为根节点是没有父亲的)
树上差分的两种基本操作用到了LCA,不了解LCA的话可以去这里面学一下
思想
类比于差分数组,树上差分利用的思想也是前缀和思想.(在这里应该是子树和思想.
当我们记录树上节点被经过的次数,记录某条边被经过的次数的时候.
如果每次强制dfs去标记的话,时间复杂度将高到爆炸!
因此我们引入了树上差分!
与树上差分在一起的使用的是 DFS ,因为在回溯的时候,我们可以计算出子树的大小.
(这个应该不用过多解释
定义数组
cnti 为节点i被经过的次数.
基本操作
1.点的差分
这个比较简单,所以先讲这个qwq
例如,我们从s−−>t ,求这条路径上的点被经过的次数.
很明显的,我们需要找到他们的LCA,(因为这个点是中转点啊qwq.
我们需要让cnt s++ ,让 cnt t++,而让他们的cnt lca−−,cnt faher(lca)−− ;
可能读着会有些难理解,所以我准备了一个图qwq。绿色的数字代表经过次数.
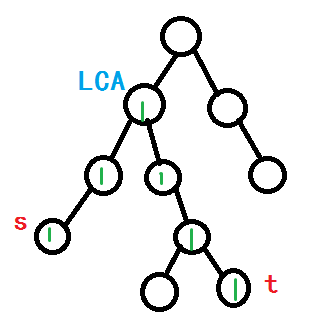
直接去标记的话,可能会T到不行,但是我们现在在讲啥?树上差分啊!
根据刚刚所讲,我们的标记应该是这样的↓
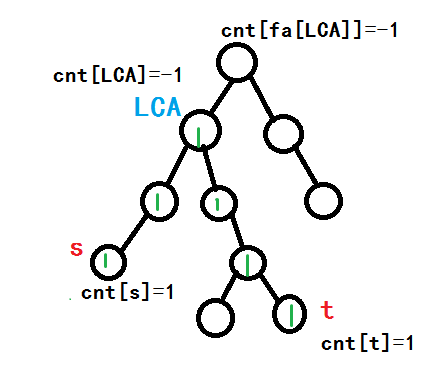
考虑:我们搜索到s,向上回溯.
下面以 u 表示当前节点, soni 代表i的儿子节点.(如果一些 son 不给出下标,即代表当前节点 u 的儿子
每个 u 统计它的子树大小,顺着路径标起来.(即cnt u+=cnt son )
我们会发现第一次从s回溯到它们的LCA时候,cnt LCA+=cnt[sonLCA]
cntLCA=0 ! "不是LCA会被经过一次嘛,为什么是0!"
别急,我们继续搜另一边.
继续:我们搜索到t,向上回溯.
依旧统计每个u的子树大小 cnt u+=cnt son
再度回到 LCA 依旧 是 cntLCA+=cnt[sonLCA]
这个时候cntLCA=1 这就达到了我们要的效果 (是不是特别优秀 ( • ̀ω•́ )✧
担忧: 万一我们再从 LCA 向上回溯的时候使得其父亲节点的子树和为1怎么办?
这样我们不就使得其父亲节点被经过了一次? 因此我们需要在cnt faher(lca)−−
这样就达到了标记我们路径上的点的要求! 厉不厉害 (o゚▽゚)o tql!!
2.边的差分
既然我们已经get到了点的差分,那么我们边的差分也是很简单啦!
机房某dalao:"这不和点差分标记方式一样吗?不就是把边塞给点吗? 看我切了它!"
为这位大佬默哀一下 qwq.
的确,我们对边进行差分需要把边塞给点,但是,这里的标记并不是同点差分一样.
PS: 把边塞给点的话,是塞给这条边所连的深度较深的节点. (即塞给儿子节点
先请大家思考 5s ……
好,时间到,有没有想到如何标记?(只要画图模拟一下就可以啦! 上图! 红色边为需要经过的边,绿色的数字代表经过次数
正常的话,我们的图是这样的.↓
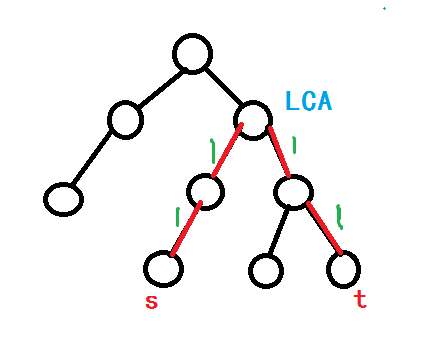
但是由于我们把边塞给了点,因此我们的图应该是这样的↓
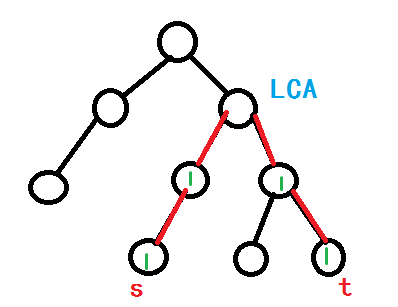
但是根据我们点差分的标记方式来看的话显然是行不通的,
否则atherLCA−−>LCA 这一路径也会被标记为经过了1次
因此考虑如何标记我们的点,来达到经过红色边的情况
聪明的你一定想到了,这样来标记
cnts++ ,cntt++ ,cntLCA−=2
这样回溯的话,我们即可只经过图中红色边啦!(这里就不详细解释啦,原理其实相同 qwq
把边塞入点中的代码这样写.qwq(顺便在搜索的时候处理即可

1 前置知识
2 需要知道的树的性质:
3
4 树上任意两个点的路径唯一.
5
6 任何子节点的父亲节点唯一.(可以认为根节点是没有父亲的)
7
8 如果你认为你知道了这些你就能秒切这些树上差分的题,那你就太低估这个东西了!
9
10 树上差分的两种基本操作用到了LCA,不了解LCA的话可以去这里面学一下
11
12 思想
13 类比于差分数组,树上差分利用的思想也是前缀和思想.(在这里应该是子树和思想.
14
15 当我们记录树上节点被经过的次数,记录某条边被经过的次数的时候.
16
17 如果每次强制dfs去标记的话,时间复杂度将高到爆炸!
18
19 因此我们引入了树上差分!
20
21 与树上差分在一起的使用的是 DFSDFS ,因为在回溯的时候,我们可以计算出子树的大小.
22
23 (这个应该不用过多解释
24
25 定义数组
26 cnt_icnt
27 i
28 为节点i被经过的次数.
29
30 基本操作
31 1.点的差分
32 这个比较简单,所以先讲这个qwq
33
34 例如,我们从 s-->ts−−>t ,求这条路径上的点被经过的次数.
35
36 很明显的,我们需要找到他们的LCA,(因为这个点是中转点啊qwq.
37
38 我们需要让 cnt_s++cnt
39 s
40 ++ ,让 cnt_t++cnt
41 t
42 ++ ,而让他们的 cnt_{lca}--cnt
43 lca
44 −− , cnt_{faher(lca)}--cnt
45 faher(lca)
46 −− ;
47
48 可能读着会有些难理解,所以我准备了一个图qwq
49
50 绿色的数字代表经过次数.
51
52
53
54 直接去标记的话,可能会T到不行,但是我们现在在讲啥?树上差分啊!
55
56 根据刚刚所讲,我们的标记应该是这样的↓
57
58
59
60 考虑:我们搜索到s,向上回溯.
61
62 下面以 uu 表示当前节点, son_ison
63 i
64 代表i的儿子节点.(如果一些 sonson 不给出下标,即代表当前节点 uu 的儿子
65
66 每个 uu 统计它的子树大小,顺着路径标起来.(即 cnt_u+=cnt_{son}cnt
67 u
68 +=cnt
69 son
70 )
71
72 我们会发现第一次从s回溯到它们的LCA时候, cnt_{LCA}+=cnt[son_{LCA}]cnt
73 LCA
74 +=cnt[son
75 LCA
76 ]
77
78 cnt_{LCA}=0cnt
79 LCA
80 =0 ! "不是LCA会被经过一次嘛,为什么是0!"
81
82 别急,我们继续搜另一边.
83
84 继续:我们搜索到t,向上回溯.
85
86 依旧统计每个u的子树大小 cnt_u+=cnt_{son}cnt
87 u
88 +=cnt
89 son
90
91
92 再度回到 LCALCA 依旧 是 cnt_{LCA}+=cnt[son_{LCA}]cnt
93 LCA
94 +=cnt[son
95 LCA
96 ]
97
98 这个时候 cnt_{LCA}=1cnt
99 LCA
100 =1 这就达到了我们要的效果 (是不是特别优秀 ( • ̀ω•́ )✧
101
102 担忧: 万一我们再从 LCALCA 向上回溯的时候使得其父亲节点的子树和为1怎么办?
103
104 这样我们不就使得其父亲节点被经过了一次? 因此我们需要在 cnt_{faher(lca)}--cnt
105 faher(lca)
106 −−
107
108 这样就达到了标记我们路径上的点的要求! 厉不厉害 (o゚▽゚)o tql!!
109
110 这样点的差分应该没什么问题了吧 ,有问题可以问我的哦 qwq (如果我会的话.)
111
112 2.边的差分
113 既然我们已经get到了点的差分,那么我们边的差分也是很简单啦!
114
115 机房某dalao:"这不和点差分标记方式一样吗?不就是把边塞给点吗? 看我切了它!"
116
117 为这位大佬默哀一下 qwq.
118
119 的确,我们对边进行差分需要把边塞给点,但是,这里的标记并不是同点差分一样.
120
121 PS: 把边塞给点的话,是塞给这条边所连的深度较深的节点. (即塞给儿子节点
122
123 先请大家思考 5s5s
124
125 \vdots⋮
126
127 \vdots⋮
128
129 \vdots⋮
130
131 好,时间到,有没有想到如何标记?(只要画图模拟一下就可以啦! 上图!
132
133 红色边为需要经过的边,绿色的数字代表经过次数
134
135 正常的话,我们的图是这样的.↓
136
137
138
139 但是由于我们把边塞给了点,因此我们的图应该是这样的↓
140
141
142
143 但是根据我们点差分的标记方式来看的话显然是行不通的,
144
145 这样的话我们会经过 father_{LCA}--> LCAfather
146 LCA
147 −−>LCA 这一路径.
148
149 因此考虑如何标记我们的点,来达到经过红色边的情况
150
151 聪明的你一定想到了,这样来标记
152
153 cnt_s++cnt
154 s
155 ++ , cnt_t ++cnt
156 t
157 ++ , cnt_{LCA}-=2cnt
158 LCA
159 −=2
160
161 这样回溯的话,我们即可只经过图中红色边啦!(这里就不详细解释啦,原理其实相同 qwq
162
163 把边塞入点中的代码这样写.qwq(顺便在搜索的时候处理即可
164
165 void dfs(int u,int fa,int dis)
166 {
167 //u为当前节点,fa为当前节点的父亲节点,dis为从fa通向u的边的边权.
168 depth[u]=depth[fa]+1;
169 f[u][0]=fa;//相信写过倍增LCA的人都能看懂.
170 init[u]=dis;//这里是将边权赋给点.
171 for(int i=1;(1<<i)<=depth[u];i++)f[u][i]=f[f[u][i-1]][i-1];//预处理倍增数组.
172 for(int i=head[u];i;i=edge[i].u)
173 {
174 if(edge[i].v==fa)continue;
175 dfs(edge[i].v,u,edge[i].w);
176 }
177 //这个每个人的写法不一样吧.
178 //所以根据每个人的代码风格不一样,码出来的也不一样
179 }
最后总结一下:
差分维护元素与它前面紧邻的一个或多个元素的逻辑关系,而且一般都可从边界由差分维护的逻辑关系推出每一个元素。(结构不只局限于线性,逻辑关系不只局限于减法的差关系、异或等)
(应用)差分经常用于优化修改相邻元素的操作,而且往往优化的效果很赞(直接到O(1)),但要O(n)处理出差分的前缀和后才能查询。适用于优化一批大量的全是修改连续元素的修改操作。离线算法。常搭配前缀和,对于先修改再询问的题来说,差分O(1)处理修改,O(n)处理出前缀和,再用前缀和O(1)处理询问。
树上差分基本都会有LCA,且树上差分常常用于求经过某点或边路径的条数。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号