洛谷 桶哥的问题——吃桶——题解
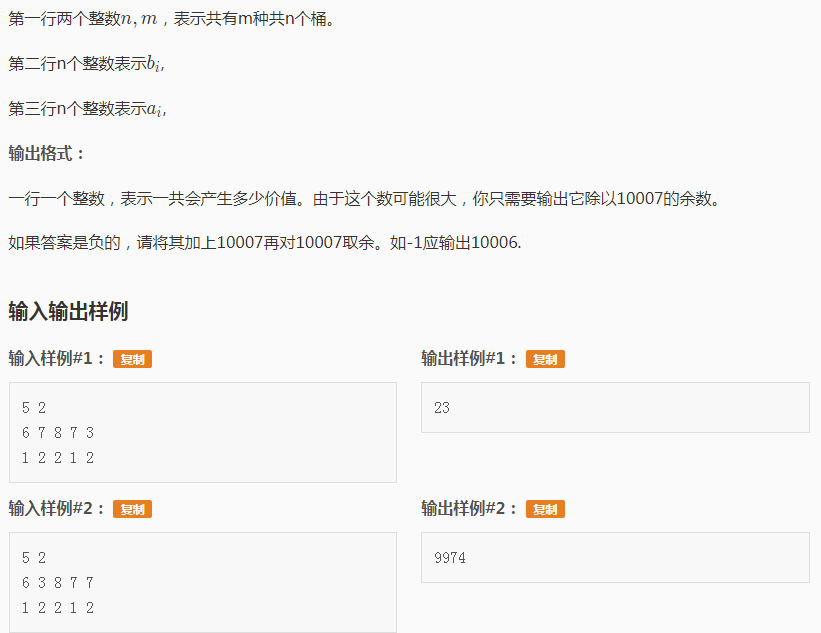
思路下限很低，暴力模拟即可，但数据很大，对时间复杂度有要求。
先分析一下题，发现核心条件即x<z且3|z-x，y并没有什么作用。同时可以证明，若x+3y=z，在z不变的情况下不会有第二对x、y满足条件，即我们找到的每个套餐都不会重复。
考虑用O（n log n）的算法。用链表的思想，把所有数据全部读完后，对每个桶来说，都从它开始往前找到第一个符合要求的桶，并让找到的桶指向它。这样处理完毕后，只需从头开始扫一遍所有桶，对每个桶来说，若桶的指针非空，就顺着指针走下去，每沿着指针走一次就是一个套餐，加到答案里即可。
可惜还是不够快，只有九十分。
代码如下：
1 // luogu-judger-enable-o2 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 #include<cctype> 7 #include<vector> 8 using namespace std; 9 vector<int>a[10001];//每个种类的集合（各元素下标） 10 int ans;char ch; 11 const long long P=10007; 12 int b[100001],zh[100001],bi[100001];//营养、种类、种类里的下标 13 int nxt[100001];//下一个 14 int reans; 15 inline int read() 16 { 17 ans=0; 18 ch=getchar(); 19 while(!isdigit(ch)) ch=getchar(); 20 while(isdigit(ch)) ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); 21 return ans; 22 } 23 int w; 24 int main() 25 { 26 // freopen("data1.in.txt","r",stdin); 27 int n=read(),m=read(); 28 for(register int i=1;i<=n;i++) 29 b[i]=read(); 30 for(register int i=1;i<=n;i++) 31 { 32 zh[i]=read(); 33 a[zh[i]].push_back(i); 34 bi[i]=a[zh[i]].size()-1; 35 for(int j=bi[i]-1;j>=0;j--) 36 { 37 if((i-a[zh[i]][j])%3==0) 38 { 39 nxt[a[zh[i]][j]]=i; 40 break; 41 } 42 } 43 } 44 int y; 45 long long an; 46 for(int i=1;i<=n;i++) 47 { 48 for(int j=nxt[i];j<=n&&j;j=nxt[j]) 49 { 50 an=(i+j)*(long long)(b[i]-b[j]); 51 reans=(reans+an)%P; 52 } 53 } 54 if(reans<0) reans+=P; 55 printf("%d",reans); 56 return 0; 57 }
_rqy提供了一种快到飞起的O（n）的算法 2095ms =》87ms 大佬就是大佬呵。。。
把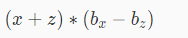
拆开，就是x*bx-x*bz+z*bx-z*bz。发现当z等于某个值时，ans就要加上所有在z前面、与z差3的倍数、与z属于同一类的x分别代入该式子得到的结果的和，写成一个算式就是∑xbx-bz∑x+z∑bx-zbz*∑1(即合法的x的个数)，设每项的∑分别为sxbx,sx,sbx,s，发现每项又可递推求出，这样一个O(n)算法就诞生了！
AC代码如下：
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cctype> 5 #include<ctime> 6 using namespace std; 7 const int mod=10007; 8 int sx[100001],sbx[100001],sxbx[100001],s[100001],a[100001],b[100001]; 9 int ans; 10 char ch; 11 inline int read() 12 { 13 ans=0; 14 ch=getchar(); 15 while(!isdigit(ch)) ch=getchar(); 16 while(isdigit(ch)) ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); 17 return ans; 18 } 19 int main() 20 { 21 int n; 22 n=read();read();//m其实并没用 23 for(int i=1;i<=n;i++) b[i]=read()%mod; 24 for(int i=1;i<=n;i++) a[i]=read(); 25 ans=0; 26 for(int gro=1;gro<=3;gro++)//差三的倍数的分一组，共有三组：%3=0的；%3=1的和%3=2的。 27 { 28 memset(sx,0,sizeof sx); 29 memset(sbx,0,sizeof sbx); 30 memset(sxbx,0,sizeof sxbx); 31 memset(s,0,sizeof s); 32 for(int z=gro;z<=n;z+=3) 33 { 34 ans=(ans+sxbx[a[z]])%mod; 35 ans=(ans-b[z]*sx[a[z]]%mod)%mod; 36 ans=(ans+z*sbx[a[z]])%mod; 37 ans=(ans-z*b[z]%mod*s[a[z]])%mod; 38 sxbx[a[z]]=(sxbx[a[z]]+z*b[z]%mod)%mod; 39 sx[a[z]]=(sx[a[z]]+z)%mod; 40 s[a[z]]=(s[a[z]]+1)%mod; 41 sbx[a[z]]=(sbx[a[z]]+b[z])%mod; 42 } 43 } 44 if(ans<0) ans+=mod; 45 printf("%d",ans); 46 return 0; 47 }
