<知识整理+注解>2019qbxt提高储备D5+后继补充 (即各种图论)
今天主讲图论。
前言:图的定义:图G是一个有序二元组(V,E),其中V称为顶集(Vertices Set),E称为边集(Edges set),E与V不相交。它们亦可写成V(G)和E(G)。
一、图的存储:
1、邻接矩阵:

2、邻接表:
数组模拟链表实现:记录每条边的终点、边权(如果有的话)、同一起点的上一条边的编号,并记录以每个点为起点的最后一条边的编号。
STL中的vector:记录以每个点为起点的边。

一些vector的细节:
vector 本质就是 c++ 模板库帮我们实现好的可以变长的数组
向一个数组(vector型) a 的末尾加入一个元素 x a.push_back(x)
询问 a 的长度 a.size(),询问a的真实长度a.capacity()
注意:vector 中元素下标从 0 开始,当需要变长时,变长一倍,因此需要额外的内存空间。
深入学习:https://www.cnblogs.com/zhonghuasong/p/5975979.html
代码:
邻接表:
const int N = 5005;//最多N个点/边
struct edge {
int u, v, w, next;//起点,终点,边权,同起点的上一条边的编号
}edg[N];
int head[N]; //以每个点为起点的最后一条边的编号
int n, m, cnt; //cnt: 边的总数
void add(int u, int v, int w)
{
int e = ++cnt;
edg[e] = (edge){u, v, w, head[u]};
head[u] = e;
}
int main()
{
cin >> n >> m; cnt = 0;
for (int u, v, w, i = 1; i <= m; i++)
cin >> u >> v >> w, add(u, v, w), odeg[u]++, ideg[v]++;
return 0;
}vector:
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 const int N = 5005;
6
7 struct edge {
8 int u, v, w;
9 };
10 vector<edge> edg[N];
11 int n, m, cnt; //cnt: numbers of edges
12 bool visited[N];
13
14 void add(int u, int v, int w)
15 {
16 edg[u].push_back((edge){u, v, w});
17 }
18 void travel(int u, int distance)//遍历
19 {
20 cout << u << " " << distance << endl; visited[u] = true;
21 for (int e = 0; e < edg[u].size(); e++)
22 if (!visited[edg[u][e].v])
23 travel(edg[u][e].v, distance + edg[u][e].w);
24 }
25 int main()
26 {
27 cin >> n >> m; cnt = 0;
28 for (int u, v, w, i = 1; i <= m; i++)
29 cin >> u >> v >> w, add(u, v, w);
30 return 0;
31 }
32 二、生成树

最小生成树:给定一个 n 个点 m 条边的带权无向图,求一个生成树,使得生成
树中边权和的最小。
例题引入:

扩展(引用百度百科):
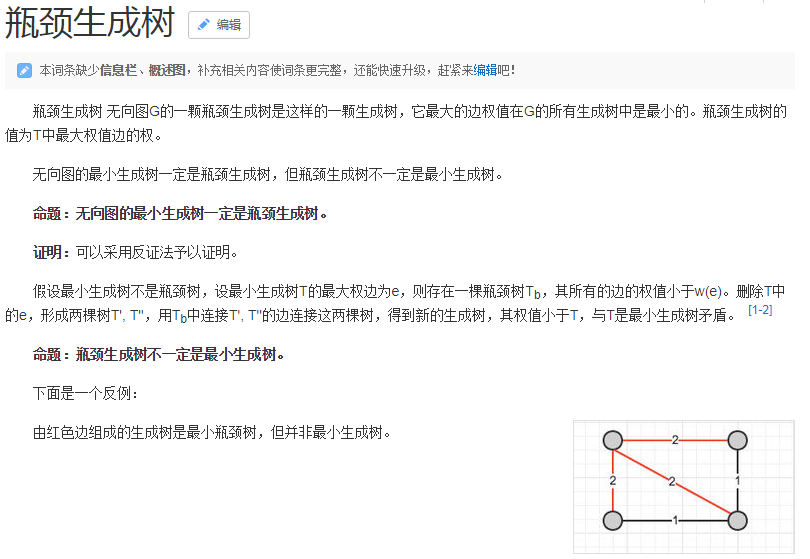
只要求出最小生成树就好了。
求解最小生成树:
生成树的本质:选取若干条边使得任意两点连通。
各种求解算法的本质:贪心
下面2个求解最小生成树算法都没有边权条件限制。
1、Kruskal算法(克鲁斯卡尔算法):
将所有边按边权排好序,从最小的开始枚举:若加入该边后,会形成环(即边的端点已经连通),就忽略掉它,看下一条;否则加入该边,直至得到最小生成树(能得到的话)。查询两点连通情况:并查集。
时间复杂度:O(E log E)
代码:
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 const int maxn = 1000005;
6 struct edge {
7 int u, v, w;
8 }edg[maxn];
9 int n, m, p[maxn], ans = 0;
10
11 bool cmp(edge a, edge b)
12 {return a.w < b.w;}
13 int findp(int t)
14 {return p[t] ? p[t] = findp(p[t]) : t;}
15 bool merge(int u, int v)
16 {
17 u = findp(u); v = findp(v);
18 if (u == v) return false;
19 p[u] = v; return true;
20 }
21 int main()
22 {
23 cin >> n >> m;
24 for (int i = 1, u, v, w; i <= m; i++)
25 cin >> u >> v >> w, edg[i] = (edge){u, v, w};
26 sort(edg + 1, edg + m + 1, cmp);
27
28 for (int i = 1; i <= m; i++)
29 if (merge(edg[i].u, edg[i].v))
30 ans = max(ans, edg[i]. w);
31 cout << ans << endl;
32 }一点口胡:“成环”的实质是边的两端点已经这通,那这条边连不连都不会改变目前的连通性了,不要错误的认为有环才是连通。除非是有向图,所以注意无向图和有向图的区别还是挺大的。
2、Prim算法(普里姆算法):
以一点为最小生成树的根,找到一个到该最小连通块边权最小、不在该连通块里的点,并加入到该连通块,直到组成最小生成树。
有一个性质:当前已确认的连通块u与外界所连的所有边中权值最小的那条x一定会被确认(如有多条,随便选其中的一条就好)。
证明很简单,若x没被确认,那么将外界确认的与u连的边y(由树的性质知y有且只有一条)换成x,则总代价会更优,与生成树总代价最小矛盾,故x一定会被选中。
易知prim算法的正确性。
时间复杂度:O(n2)
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#define forup(i,n) for(int i=1;i<=n;i++)//偷懒
using namespace std;
int n,m;
int ma[5001][5001],bianli=1,d[5001];
bool vis[5001];
int main()
{
int x,y,z,tot=0;
cin>>n>>m;
memset(ma,0x3f,sizeof(ma));//求最短性图论问题一般初始化为一个很大的数
forup(i,m)
{
scanf("%d%d%d",&x,&y,&z);//去重边
if(z<ma[x][y])
ma[x][y]=ma[y][x]=z;
}
vis[1]=1;
memset(d,0x3f,sizeof(d));
d[1]=0;
memset(vis,0,sizeof(vis));//0蓝1白
int stt_node,stt_dis;
forup(i,n)
{
stt_dis=0x3f3f3f3f,stt_node=0;
for(int j=1;j<=n;j++)
if(!vis[j]&&d[j]<stt_dis)
{
stt_node=j;
stt_dis=d[j];
}
vis[stt_node]=1;
tot+=stt_dis;
for(int j=1;j<=n;j++)
if(!vis[j]&&d[j]>ma[j][stt_node])
{
d[j]=ma[j][stt_node];
}
}
cout<<tot;
return 0;
}可用堆优化,复杂度O(n log m + m)。
最小生成树的性质:https://blog.cswdn.net/zengchen__acmer/article/details/17323245
更多扩展:https://oi-wiki.org/graph/mst/#_16
注意点/注释:
严格次小生成树代码部分:
注意严格次大值==最大值时要不断往下找严格小于最大值的次大值。
利用排序,省了很多分类,不错。
注意严格次大值可能没有的情况,不能就这么减-INF了。
瓶颈生成树因为连通,故一定会有连着最小生成树删边后两部分的边。
三、路径
最短路径问题:
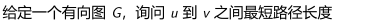

最短路径算法主要操作:不断进行松弛操作(更新最短路操作)
限制:不能有负权回路,否则负权回路参与松弛后得到的答案就不正确。
1、Floyd算法(弗洛伊德算法):
本质思想:动态规划。
设dp[i][j][k]为中间节点(不包括起止点)只经过1~k时i到j的最短路长度,初始dp[i][j][0]=边(i,j)的长度(没有则为正无穷)。
对于dp[i][j][k],若i到j的最短路中间节点只考虑1~k时要么经过了k,为dp[i][k][k-1]+dp[k][j][k-1],要么没经过k为dp[i][j][k-1],有这两种情况。取较小值,得转移方程dp[i][j][k]=min(dp[i][j][k-1],dp[i][k][k-1]+dp[k][j][k-1]),这样当前k的i,j都看完后,若有中间节点就只经过了1~k的最短路u,那么其答案就得出了(因为u的中间节点只经过1~k,那么最短路径(i,k)和(k,j) (这两个路径组成(i,j))的中间节点必定只能经过1~(k-1),若k-1的答案的得出,k的答案就能得出,而k=0时的边界已有,那么k就能逐层递推不断变大了,不用管那些没有意义的量,因为最后的答案都是由有意义的量推出来的,同理 状态转移时关注这些有意义的量就好,无意义的量只会 在过程中被取代、混淆视听,只要保证最后答案有意义就不用管无意义的量了。),当k取到n时,最终答案就有了。
对于路径保存,可以建个二维数组nxt[i][j]表示最短路(i,j)的起点i的后继,初始化:读入边(i,j)时nxt[i][j]=j。在每次松弛时修改nxt[i][j]=nxt[i][k]。输出时:i,nxt[i][j],nxt[nxt[i]][j],……
发现k在dp过程中作为第一重循环,单调递增,尝试分析转移顺序,能否利用滚动数组将空间由n^3优化为n^2:对于转移方程dp[i][j][k]=min(dp[i][j][k-1],dp[i][k][k-1]+dp[k][j][k-1]),k>i,j时没有问题;k<i或j时,dp[i][k]或dp[k][j]已经在这一层循环中求过,第三维实际上已变成k,但没有关系,最短路(i,k)和(k,j)的中间节点一定不经过k,即dp[i][k][k-1]==dp[i][k][k],dp[k][j]同理,故可以用滚动数组优化空间。
应用:可求任意两点之间的最短路(多源最短路),时间复杂度O(n^3)。限制:图可有负权边,但不能有负权回路(有负权回路的话就没有最短路了)。
检测负权环(负权回路):

d(u,u)<0即有一条从u开始最后到达u的负权路径,即一条负权回路。
有负环时floyd得出的答案只会小于等于 一条边只经过一次的最短路的真值, 不一定能算出真正的答案,这个算法不能一定正确,就大大减少了此情景下的实用价值。一个Floyd错误的原因,也是例子:
设一负权环上编号最大的点为u,则最迟当k=u-1时dp[u][u]已经得出结果且小于0、小于等于答案,那么当k=u时,所有dp[i][u]和dp[u][i]都会因松弛操作而减少(程序发现可走一个u为起、终点的负环),而i又可以作为之后的k,这就不正确(不是一条边只经过一次的最短路)了。
代码(循环顺序影响结果正确性,不能变):
1 int d[N][N], n, m;
2 int main()
3 {
4 cin >> n >> m;
5 for (int i = 1; i <= n; i++)
6 for (int j = 1; j <= n; j++) d[i][j] = inf;
7 for (int u, v, w, i = 1; i <= m; i++)
8 cin >> u >> v >> w, d[u][v] = min(d[u][v], w);
9
10 for (int k = 1; k <= n; k++)
11 for (int i = 1; i <= n; i++)
12 for (int j = 1; j <= n; j++)
13 d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
14 }一个应用:
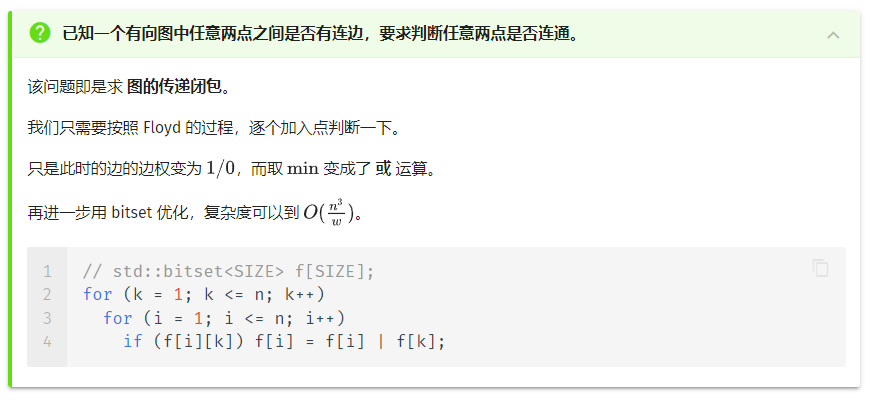
讲下代码:f[i]为一组bitset。f[i][j]依旧表示i,j的连通关系。k,i,j的意义不变。枚举到k,i时,f[i][k]连通,才能用f[i][k]和f[k][j]更新f[i][j]。由于无向图连通性,f[k][j]==f[j][k]。故当f[i][k]==1时可直接f[i]=f[i] | f[k] ,即f[i][j]看对应列的f[k][j]。
2、Bellman-Ford算法(贝尔曼-福特算法)
单源最短路算法,设源点为S,图有n个点m条边

正确性:
d[u]经过几条边,就最多用几次全局松弛后一定能得到真实值(最优子结构)。任意最短路经过不超过 n − 1 条边,n-1 次松弛足矣。

先提一句,nm的时间复杂度为最坏情况的上限/有负环时的情况,最好情况下时间复杂度只有O(n)(一次全局松弛的松弛顺序正好可以一点接一点求出所有d[u],这种情况也是下文spfa期望的)。若没有负权环,则n-1次全局松弛求出所有d[u],再松弛也不会变化。只有存在负环时才继续变化。因此不适用于有负权环时求最短路的情况。
易知如果所有d(u) 在上一次全局松弛中都没有被更新,那么答案就求出,不必继续松弛了。
代码:
1 struct edge{
2 int u, v, w;
3 }edg[N];
4 int d[N], n, m, S;
5 int main()
6 {
7 cin >> n >> m >> S;
8 for (int i = 1; i <= n; i++) d[i] = inf;
9 for (int u, v, w, i = 1; i <= m; i++)
10 cin >> u >> v >> w, edg[i] = (edge){u, v, w};
11
12 d[S] = 0;
13 for (int i = 1; i <= n; i++)
14 for (int j = 1; j <= m; j++)
15 {
16 int u = edg[j].u, v = edg[j].v, w = edg[j].w;
17 d[v] = min(d[v], d[u] + w);
18 }
19 }用来判负环时要注意源点问题。
3.SPFA算法(Shortest Path Faster Algorithm 翻译:最短路径快速算法(在一般情况下的确挺快的,只要不被针对))
Bellman-Ford 算法中,对于这次要松弛的边,当它的起点有被松弛过时,这次松弛才是有意义的,可见有很多无用的松弛操作。
spfa就是贝尔曼-福特算法的队列优化形式,通过队列存储松弛过的点减少了很多无意义的松弛,时间复杂度O(kE)(k是小常数,平均值为2)最糟糕的时间复杂度O(VE)(被针对的恐惧)常见卡spfa方法
当E本身就非常大时(稠密图)就不好用了。


代码:
1 struct edge{
2 int u, v, w;
3 };
4 vector<edge> edg[N];
5 int d[N], n, m, S;
6
7 queue<int> Queue;
8 bool inQueue[N];
9 int cntQueue[N];
10
11 void add(int u, int v, int w)
12 {
13 edg[u].push_back((edge){u, v, w});
14 }
15 int main()
16 {
17 cin >> n >> m >> S;
18 for (int i = 1; i <= n; i++) d[i] = inf;
19 for (int u, v, w, i = 1; i <= m; i++)
20 cin >> u >> v >> w, add(u, v, w);
21
22 d[S] = 0; inQueue[S] = true; Queue.push(S);
23 while (!Queue.empty())
24 {
25 int u = Queue.front(); Queue.pop(); inQueue[u] = false;
26 for (int e = 0; e < edg[u].size(); e++)
27 {
28 int v = edg[u][e].v, w = edg[u][e].w;
29 if (d[v] > d[u] + w)
30 {
31 d[v] = d[u] + w;
32 if (!inQueue[v])
33 {
34 Queue.push(v); ++cntQueue[v]; inQueue[v] = true;
35 if (cntQueue[v] >= n) {cout << "Negative Ring" << endl; return 0;}//是负权环
36 }
37 }
38 }
39 }
40 for (int i = 1; i <= n; i++)
41 cout << d[i] << endl;
42 }
4.Dijkstra算法( 迪杰斯特拉算法)
一个单源最短路算法。
知道d(u) 被更新成真实值之前,u 出边的松弛操作都无意义。以一个点为源点,设d[i]为i节点到根的最短距离。将d初始化(有与源点连边的为边的边权,否则为很大的数),找到最小的d[i]且i未被确定,将i节点标记为已确定最短路,并更新i节点出边终点的d。重复以上过程至所有点都被确定。
时间复杂度 O(n 2 + m)
代码:
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 const int N = 1e5 + 5;
6 const int inf = 1 << 29;
7
8 struct edge{
9 int u, v, w;
10 };
11 vector<edge> edg[N];
12 int d[N], n, m, S;
13
14 bool relaxed[N];
15
16 void add(int u, int v, int w)
17 {
18 edg[u].push_back((edge){u, v, w});
19 }
20 int main()
21 {
22 cin >> n >> m >> S;
23 for (int i = 1; i <= n; i++) d[i] = inf;
24 for (int u, v, w, i = 1; i <= m; i++)
25 cin >> u >> v >> w, add(u, v, w);
26
27 d[S] = 0;
28 for (int i = 1; i <= n; i++)
29 {
30 int u = 1; while (relaxed[u]) ++u;//找到第一个没有被确定的点
31 for (int j = 1; j <= n; j++)//找到d[i]最短且未被确定的i
32 if (!relaxed[j] && d[j] < d[u]) u = j;
33 relaxed[u] = true;
34 for (int e = 0; e < edg[u].size(); e++)//进行松弛操作
35 {
36 int v = edg[u][e].v, w = edg[u][e].w;
37 d[v] = min(d[v], d[u] + w);
38 }
39 }
40 for (int i = 1; i <= n; i++)
41 cout << d[i] << endl;
42 }
EX:Dijkstra堆优化
利用小根堆的性质节省找到d[i]最小且未被确定的i的时间。


代码:
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 const int N = 1e5 + 5;
6 const int inf = 1 << 29;
7
8 struct edge{
9 int u, v, w;
10 };
11 vector<edge> edg[N];
12 int d[N], n, m, S;
13
14 bool relaxed[N];
15 struct Qnode {
16 int u, du;
17 bool operator<(const Qnode &v)
18 const {return v.du < du;}//不加const会出错
19 };
20 priority_queue<Qnode> PQueue;
21
22 void add(int u, int v, int w)
23 {
24 edg[u].push_back((edge){u, v, w});
25 }
26 int main()
27 {
28 cin >> n >> m >> S;
29 for (int i = 1; i <= n; i++) d[i] = inf;
30 for (int u, v, w, i = 1; i <= m; i++)
31 cin >> u >> v >> w, add(u, v, w);
32
33 d[S] = 0; PQueue.push((Qnode){S, 0});
34 while (!PQueue.empty())
35 {
36 int u = PQueue.top().u; PQueue.pop();
37 if (relaxed[u]) continue;
38 //if edges staring from u are already relaxed, no need to relax again.
39 relaxed[u] = true;
40 for (int e = 0; e < edg[u].size(); e++)
41 {
42 int v = edg[u][e].v, w = edg[u][e].w;
43 if (d[v] > d[u] + w)
44 {
45 d[v] = d[u] + w;
46 PQueue.push((Qnode){v, d[v]});
47 //if d(v) is updated, push v into PQueue
48 }
49 }
50 }
51 for (int i = 1; i <= n; i++)
52 cout << d[i] << endl;
53 }每个点被确认答案时会看一遍所有出边,对有向图,每个边只会看一次。共确定n个点,时间复杂度O(nlog(n+m)),无向图每个边会看两次,常数乘个2差不多了。
后来思考的一点扩展:最短路后记
另外的扩展:https://oi-wiki.org/graph/shortest-path/
注意点:
floyd求最小环:总会出现(u,x)和(u,y)为一条边的情况,不会使答案错误。
Johnson 全源最短路径算法把新图求最短路对应到原图,并使边权非负从而可用dijkstra。
k短路问题:https://oi-wiki.org/graph/kth-path/
简单说即用A*找第k次最短路。
A*算法“为什么第k次出队的结果即为答案”的原理/解释:f(x)=g(x)+h(x)可以理解为当前走到g(x)所代表的路径而到了x点的情况下,最短路为多少。设源点为s,则初始的f(s)=g(s)+h(s)即代表了所有路径(所有路径都从源点出发),显然全局最短路包含在内,接下来不断取出最优的f(x),运行算法,直至取完一条最短路,t点出队一次后,此时优先队列里所有的状态即代表了除了这条最短路的路径以外的其他所有路径的情况,也一定包含次短路,而这个次短路,一定是某个g(x)+h(x)所构成的,同时也是队首的元素,取出这条次短路后,队列里状态即代表了所有除了最短路与次短路的路径以外的情况(经过点一样但有点的经过次数不一样的两条路径被视为不同路径),可见算法是从所有转移到的情况(也是所有情况)/路径中从小到大取出路径(s,t),即t第k次出队时的路径即为k短路。
同时对于中间点,当他第y次出队时,此时g(y)即是(s,y)的第y短路:对于当前被取出的点x,由于它的f(x)=g(x)+h(x)在当前最小,而h(x)必然最小,则g(x)在当前已取出几条最短路径的情况下的也是最小,即g(x)是当前情况下的s到x的最短路。即当我们访问到一个结点第k次时,对应的状态的g(x)就是从s 到该结点的第k短路。类似的很多别人的文章都有这个说法:对于dijstra算法,有一个结论就是,当一个点第k次出队的时候,此时路径长度就是s到它的第k短路。证明方法同上行,甚至因为有边权都是非负的性质,还更好证。
对于一个点出队大于k次就不用更新子状态,不用担心一条路径重复经过一个节点导致丢失答案的情况。h(x)中除了开头的x,不会再经过x点。对于一条路径上第二次经过x点,第一次经过x而出队时,那时的g(x)会配合h(x)产生一次答案,故答案不会丢失。
差分约束:求出最短路后,三角不等式d[u]+w>=d[v]。刚好是约束的条件。
有s向所有点连一条权值为0的出边。s只向外连出边,故不会参与成环,只要求出一种形式的最短路,三角不等式既满足。对于原图不连通的块,新图也不连通(s没有入边),故不影响块间的独立性。
三、DAG(有向无环图)
任意一个DAG一定有出度为0的点和入度为0的点。一个DAG删去一点后仍是DAG
1、拓补排序(topsort)
n个点的DAG一定存在拓补序列。
按照有向图中边的起点一定在终点之前的顺序给出一个可行的节点序列(多数不唯一)
换个角度:

实现:
1、
找到 DAG 中入度为 0 的点 u,u 可以放在当前 DAG 拓扑序末尾将 v 和与 v 有关的连边从 DAG 中删除
2、广搜:从入度为


 浙公网安备 33010602011771号
浙公网安备 33010602011771号