快晴的线段树小杂烩Ciallo~⭐
线段树,有什么用?
在计算机计算的过程当中,我们很多时候都要去解决一些连续区间的问题,包含且不仅局限于RMQ问题,就譬如求连续区间的GCD。更直接地,它可以很方便用于计算几何的维护。
区间和问题。
有一张很长很长的试卷,老师好不容易批改完成了。这时他要去统计该试卷的分数,因为试卷很多很长,他想写一个程序,尽可能快的统计一张试卷上任意连续题号的总分数,他把这个任务交给了聪明的你。
暴力的想总共存在\(Q\)个询问,我们对于每一个询问,我们会花费\(O(n)\)的时间进行扫描,求解。很多人会想复杂度就此了,就这样用它似乎也没什么不好。就这样,我们只是花费了\(O(Q*n)\)的时间复杂度去处理该问题。即使数据范围不是充分大,你的程序还是,很慢。
怎样去设计算法,降低时间复杂度呢?前缀和呼之欲出。连续区间的和是连续的,意思也就是\(sum[r]\)=\(a[1]+a[2]+...+a[r]\),显然,有\(sum[k]-sum[k-1]\)=\(a[k]\)。综上所述,我们只要维护\(n\)个前缀和,甚至可以在\(O(1)\)的时间内回答每一个询问!
区间修改问题
偶然的,老师发现评分标准出现了误差,在某些连续题号出现了少(多)加\(a\)分的情况。他想写为以上程序添加修改连续区间的功能,并且尽可能快的修改,他把这个任务交给了聪明的你。
区间修改...我们看了看上面的前缀和,算法大楼,轰然倒塌。
我们将问题分离,只讨论区间修改。我们可以应用差分的思想,显然,存在公式,\(sum[r]=a[1]+...+a[r]\),我们考虑有数组\(b\),\(b[i]=a[i]-a[i-1]\),我们记\(a[0]=0\),因此\(sumb[r]=b[1]+...+b[r]=a[1]+a[2]-a[1]+a[3]-a[2]...+a[r]-a[r-1]=a[r]\)
当我们\(b[i]+k\)再进行对\(b\)前缀和,有公式,\(sumb[j]=b[1]...+b[j]+k-b[j-1]=a[j]+k\) and \(j>=i\)
意思也就是我们对\(b[i]\)加上一个值\(k\)时,对于每一个\(sumb[j>=i]\)均会增加\(k\)。
同理地,我们要进行区间修改,只要在\(b[l]\)处加\(k\),且在\(b[r+1]\)减\(k\)即可。
多好的一个性质啊...如果只要求要求我们进行区间修改,也可以在\(O(1)\)的时间内实现。但是同时做,好像就不那么可行...
这时,奇迹发生了!
普通线段树+带懒标记的线段树
这里首先首先说线段树是什么,线段树是基于区间划分的二叉树。
形象的,我们如果存在"1 1 4 5 1 4 1 9 1 9 8 1 0"这个区间,我们如何划分?
我们约定对于每一个区间\(l==r\)时便不能划分。如图。
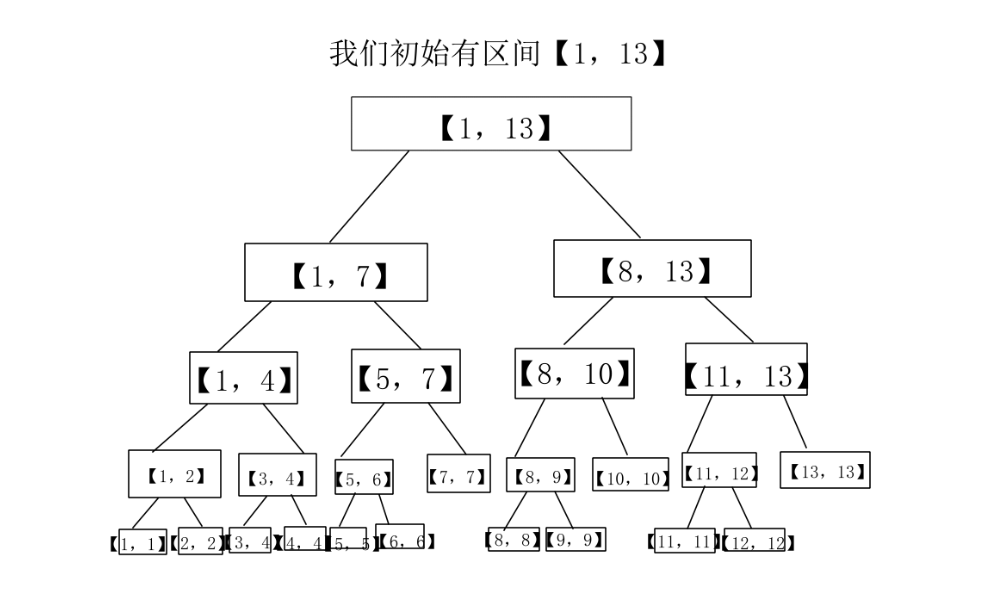
我们可以对于每一个\(mid=(l+r)/2\)划分每一个区间,每一个节点我们维护区间\([l,r]\)的和值,以及所代表的区间\(l\)及\(r\)。最终递归地,可以建立这颗二叉树。
我们可以知道,对于叶子节点,其和值为其权值,但是对于其父亲节点呢?
我们可以定义一个\(pushup\)操作,显然\(sum[l...r]=sum[l...k]+sum[k+1...r]\)。
因此对于每个叶子节点的父亲节点,均有\(sum[p]=sum[lson]+sum[rson]\)
因此,每一个节点维护的和值也可以通过\(pushup\)操作计算出来。
区间和问题
假设我们想要区间\([5,11]\)的和值,我们可以像搜索二叉树一样。
\(def:\) \(query(u,v,p)\)//p代表当前节点
\(if\) \(区间[l,r]全包含所求区间[u,v]\) \(return\) \(该节点维护的和值\)
\(else\) \(if\) \(区间[l,r]不全包含所求区间[u,v]\) \(return\) \(query(u,v,p*2)+query(u,v,p*2+1)\)
\(else\) \(if\) \(区间[l,r]不包含所求区间[u,v]\) \(return\) \(0\)
\(end\)
我们发现算法复杂度,它类似于二叉树的遍历,总共存在\(n\)个节点时,由于势能,我们搜索的节点会不断下沉,直到全包含或不包含时。当不全包含时,我们的搜索路径会分裂。即使这样,最多也只是搜索\(4*\log n\)个节点。因此,可以证明,复杂度是\(\log n\)的。
复杂度证明
我们只是光说\(\log\)的时间复杂度,肯定很不可信,因此我们给出严格证明。
我们只考虑最坏情况。
如何,到达最坏复杂度的情况?贪心地想,自然是访问尽可能多的点。
显然,对于每一个询问,会查找节点的左右儿子,依此迭代。
访问任意一个节点会有两种不同的选择:
①:只分裂向左或右儿子
②:左右儿子均分裂
显然,对于第二种情况,我们才能够尽可能访问多的节点。因此贪心地想,我们尽可能执行第二种操作。
最后,我们可以得到这样一颗树:
①:树的每一层的最左节点均被访问,最右节点亦然。
②:并且对于每一个分裂,会产生两个新访问的节点。因此对于每一个最左被访问节点的右兄弟也被访问,并且被完全覆盖,因此其右兄弟不再向下访问。每一个最右被访问的节点亦然。
因此可以发现访问的点数最大为\(O(4*\log n)\)个。
证毕。
例题
\(\large 130. 树状数组 1 :单点修改,区间查询\)
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=1e6+7;
int a[maxn];
struct node
{
int l,r;
ll val;
}sge[4*maxn];
void pushup(int u)
{sge[u].val=sge[u<<1].val+sge[u<<1|1].val;}
void build(int u,int l,int r)
{
int mid=l+r>>1;
sge[u]={l,r};
if(l==r){sge[u].val=a[r];return;}
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
}
ll query(int u,int l,int r)
{
int mid=sge[u].l+sge[u].r>>1;
ll ans=0;
if(l<=sge[u].l&&sge[u].r<=r)return sge[u].val;
if(l<=mid)ans=query(u<<1,l,r);
if(r>mid)ans+=query(u<<1|1,l,r);
pushup(u);
return ans;
}
void modify(int u,int x,int v)
{
int mid=sge[u].l+sge[u].r>>1;
if(sge[u].l==sge[u].r&&sge[u].l==x)
{sge[u].val+=v;return;}
if(x<=mid)modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
int main()
{
int n,q;
scanf("%d%d",&n,&q);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
build(1,1,n);
while(q--)
{
int l,r,x,t;
scanf("%d%d%d",&t,&l,&r);
if(t==1)modify(1,l,r);
else if(t==2)printf("%lld\n",query(1,l,r));
}
return 0;
}
区间修改
在看区间修改之前,我们先看一下单点修改。
我们直观的想,单点修改不就是直接修改叶子节点吗?
好,单点修改问题解决了。
和区间和问题类似的,单点修改也会在二叉树上搜索节点,可以证明,经过节点数不超过\(4*\log n\)。
那么,类似的区间修改,不就是一堆单点修改吗?
大大的×,每次修改花费\(O((r-l)*\log n)\)的复杂度显然是我们不想见到的。
既然我们维护了二叉树状的区间和,我们直接在这些区间上做修改这不香吗?
因此我们在某些父亲节点或叶子节点上全包含待修改区间时做出了区间修改。因为和区间和问题的搜索类似,其最大复杂度也不会超过\(4*\log n\)。
但是仔细想想,这不对啊。区间修改花费的时间虽然只用了\(O(\log n)\),但是当一个非叶子节点的区间\([l,r]\)被完全修改时,其子节点没有被修改。当我们去不全包含的询问到了这个区间,我们必然只能搜索其子节点。结果,我们得到了未被修改的值。答案出现了错误。
为了解决这个问题,我们引入了懒标记。
懒标记
懒标记就是你妈不到你面前叫你干活你绝不干活。——注解
上面区间修改后,我们查询区间和值遇到了什么问题?子节点存在未被修改的现象。
我们首先定义一个标记lazy,代表该节点修改过后所增加的偏移量。
既然这样,如果存在一个节点,它被修改过,并且在修改过后,它是第一次被访问到,无论是以修改还是询问区间和的方式被访问到,我们就可以将其懒标记下传给其左右儿子,将其维护的区间和值加上懒标记维护的值,并将该节点的懒标记置为0。
因为我们只有再一次访问到该节点才会下传懒标记,可以发现,它是一个不大的常数。因此对于懒标记维护的线段树,我们仍可以在近似\(\log n\)的时间内完成每一次操作。
至此,区间修改问题已经解决。
复杂度
空间复杂度:\(O(n*4-1)\)
我们这里分类讨论:
这里引入容易证明的前提,线段树的最底层节点与满节点的层数之差小于等于\(1\)。
如果为满二叉树,显然存在\(n\)个叶节点,自然有\(n-1\)个非叶节点。
否则,假设我们存在这种情况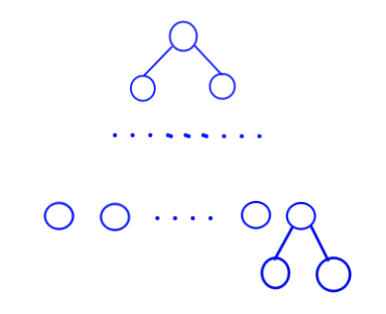
,显然,这同时也是最坏情况。我们存在\(n+1\)个叶子节点,但是我们是以数组的方式开销空间,因此最底层使用\(2*n\)的空间,倒数第二层使用\(n\)的空间,其余层使用\(n-1\)的空间。故总和为\(O(4*n-1)\)。
建树:\(O(n*\log n)\)
单点修改:\(O(\log n)\)
区间修改:\(O(\log n)\)
查询:\(O(\log n)\)
例题
$\large 243. 一个简单的整数问题2 $
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=1e6+7;
int a[maxn];
struct node
{
int l,r;
ll val,lzy;
}sge[4*maxn];
void pushup(int u)
{sge[u].val=sge[u<<1].val+sge[u<<1|1].val;}
void pushdown(int u)
{
if(sge[u].lzy)
{
sge[u<<1].lzy+=sge[u].lzy;
sge[u<<1|1].lzy+=sge[u].lzy;
int mid=sge[u].l+sge[u].r>>1;
sge[u<<1].val+=sge[u].lzy*(mid-sge[u<<1].l+1);
sge[u<<1|1].val+=sge[u].lzy*(sge[u<<1|1].r-mid);
sge[u].lzy=0;
}
}
void build(int u,int l,int r)
{
int mid=l+r>>1;
sge[u]={l,r};
if(l==r){sge[u].val=a[r];return;}
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
}
ll query(int u,int l,int r)
{
int mid=sge[u].l+sge[u].r>>1;
ll ans=0;
if(l<=sge[u].l&&sge[u].r<=r)return sge[u].val;
pushdown(u);
if(l<=mid)ans=query(u<<1,l,r);
if(r>mid)ans+=query(u<<1|1,l,r);
pushup(u);
return ans;
}
void modify(int u,int l,int r,int v)
{
int mid=sge[u].l+sge[u].r>>1;
if(l<=sge[u].l&&sge[u].r<=r)
{sge[u].val+=v*(sge[u].r-sge[u].l+1),sge[u].lzy+=v;return;}
pushdown(u);
if(l<=mid)modify(u<<1,l,r,v);
if(r>mid)modify(u<<1|1,l,r,v);
pushup(u);
}
int main()
{
int n,q;
scanf("%d%d",&n,&q);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
build(1,1,n);
while(q--)
{
int l,r,x;char t[5];
scanf("%s",t+1);
if(t[1]=='C')
{
scanf("%d%d%d",&l,&r,&x);
modify(1,l,r,x);
}
else if(t[1]=='Q')
{
scanf("%d%d",&l,&r);
printf("%lld\n",query(1,l,r));
}
}
return 0;
}
线段树维护矩阵面积并
给定n个矩阵的左下角和右上角坐标,求矩形面积并(矩阵总是正放的,即与x轴y轴都平行)
算法思想
我们存在一张直角坐标系,其上存在很多矩形。长这样。
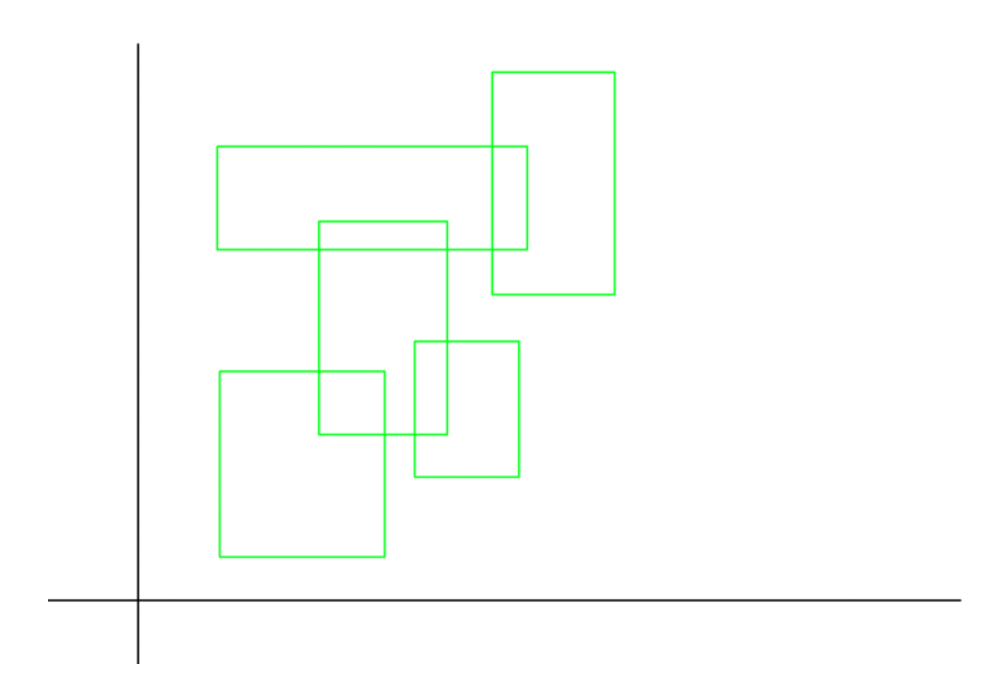
我们如果暴力的求,复杂度自然是\(O(n^2)\),当数据范围过大时,对时间资源的消耗很大。
我们考虑一个矩形的面积贡献如何形成。
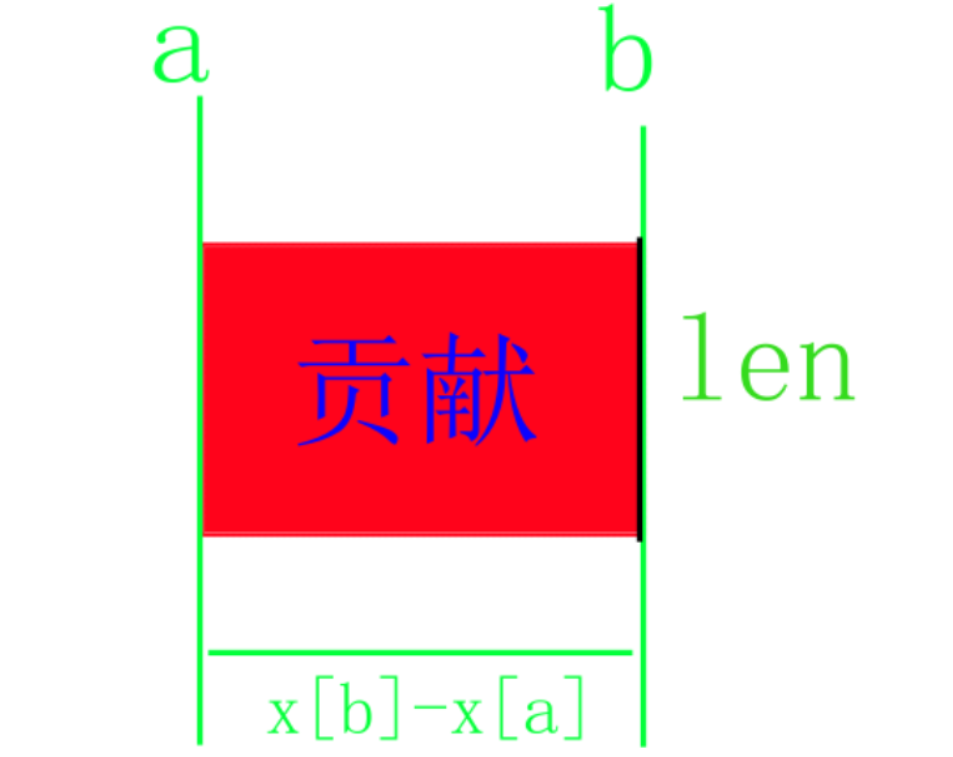
如果对于每一个\(x[b]-x[a]\)均可知,只要求出\(len\)即可快速求出对面积的贡献为\(len*(x[b]-x[a])\)
我们现在考虑多个矩形面积并怎么求?就以上图为例。
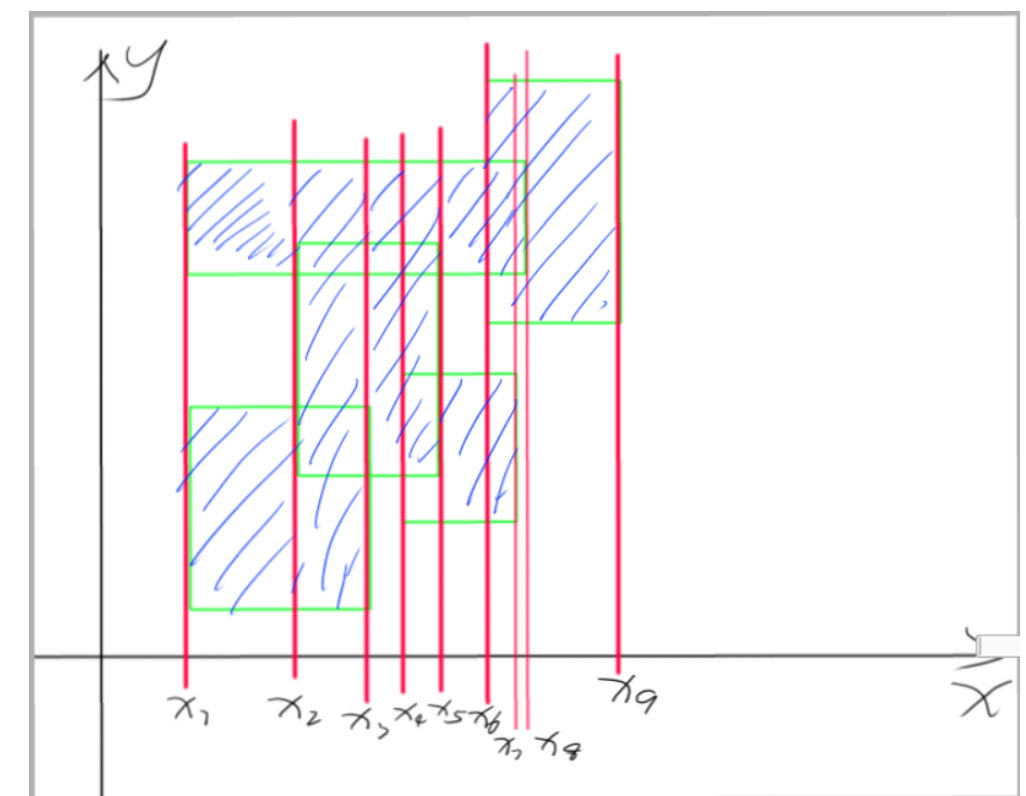
我们将矩形的按\(x\)轴上的左右边界拆出,每一个矩形可以拆出两条线段。
显然,我们如果有一条平行于\(x\)轴的直线,与任意一个矩形存在两个交点,左边一定为进入矩形,右边一定出去矩形。也就是贡献区域在进入矩形时直到刚好出矩形时。
因此我们按以上的拆分方式去枚举矩形的面积一定可行。
观察上图,我们只要枚举每一个$x[i]-x[i-1] $ and \(i>=2\),总和其中矩阵中面积(阴影部分面积),即可求出矩阵面积并。
现在的问题就是如何求出每一个$x[i]-x[i-1] \(上\)y$轴显露的长度。
抽象一点,我们在已经拆出的矩形左右边界中,能找到一批处于相同\(x\)轴位置的边界。我们现在要求这一堆边界在\(y\)上值域上的覆盖。
根据矩形的性质,因此每一个边界的\(y-low\)到\(y-top\)是连续的。也就是给我们以\(y\)的值域构成的线段树,可以对任意一个区间做加法,询问\([lowest,topest]\)上于的\(y\)轴有效线段的长度。
因此我们可以不太容易的写出以下代码。
坑点
①:当建立线段树的值域过大时,我们要考虑离散化;
②:因为一个矩形不存在\(x\)相同的左右边界,因此我们线段树建立的叶节点一定会相较于离散化的数据数少一个。因为一般的线段树是以\(l=r\)为叶节点,而我们只能以\(r-1=r\)为叶节点,因此会少一个叶节点。
复杂度
空间复杂度:这里依赖于\(y\)轴值离散化后的值域\(O(4*range-1)\)
时间复杂度:\(O(n*\log n)\)
例题
$\large 247. 亚特兰蒂斯 $
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
#include<iostream>
using namespace std;
#define pb push_back
#define lson (p<<1)
#define rson (p<<1|1)
const int rg=2e5+7;
struct node{double x,l,r;int val;
bool operator<(const node a)const
{return x<a.x;}};
struct segtree
{int l,r;double val;int flag;}seg[rg<<2];
vector<node>y;
vector<double>ydis,range;
int find(double x){return lower_bound(range.begin(),range.end(),x)-range.begin();}
void pushup(int p)
{
if(seg[p].flag)seg[p].val=range[seg[p].r+1]-range[seg[p].l];
else if(seg[p].r!=seg[p].l)seg[p].val=seg[lson].val+seg[rson].val;
else seg[p].val=0;
}
void build(int l,int r,int p)
{
if(l==r){seg[p]={r,r,0,0};return;}
int mid=l+r>>1;
build(l,mid,lson),build(mid+1,r,rson);
seg[p]={l,r,0,0};
}
void modify(int u,int v,int p,int x)
{
int l=seg[p].l,r=seg[p].r,mid=l+r>>1;
if(u<=l&&v>=r){seg[p].flag+=x,pushup(p);return;}
if(u<=mid)modify(u,v,lson,x);
if(v>mid)modify(u,v,rson,x);
pushup(p);
}
int main()
{
int n,T=0;
while(scanf("%d",&n),n)
{
++T;
y.clear(),ydis.clear(),range.clear();
for(int i=1;i<=n;++i)
{
double a,b,c,d;
cin>>a>>b>>c>>d;
ydis.pb(b),ydis.pb(d);
y.pb({a,b,d,1}),y.pb({c,b,d,-1});
}
sort(y.begin(),y.end());
sort(ydis.begin(),ydis.end());
for(int i=0;i<ydis.size();++i)
if(!i||ydis[i]!=ydis[i-1])range.pb(ydis[i]);
build(0,range.size()-2,1);
double res=0;
for(int i=0;i<y.size();++i)
{
if(i)res+=seg[1].val*(y[i].x-y[i-1].x);
modify(find(y[i].l),find(y[i].r)-1,1,y[i].val);
}
cout<<res<<'\n';
}
return 0;
}
ZKW线段树
引入
这里难以做出完备的介绍,有兴趣者可以参考清华大学张昆玮(ZKW)本人的教学PPT——《统计的力量》
我们考虑,一般的线段树是之上而下的建树,并且在一系列的操作中调用了很多次递归,导致其常数特别大,并且空间开销也比较巨大。
我们想,有没有一种方法可以优化线段树呢?既然有DFS,那么就有BFS;既然有递归,那么必然也有迭代。
上述变化是等价的,因此,我们想,有没有用迭代的思想写出线段树,减少递归造成的时间开销?
因为线段树是一颗二叉树,因此类似的,我们可以有这么一颗完全二叉树。
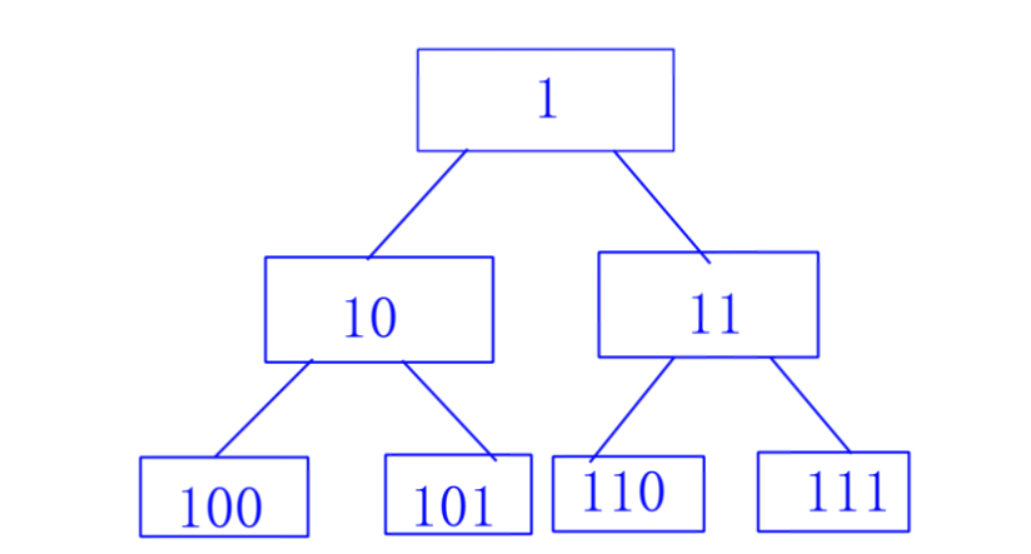
每一个线段树都可以表示成这样现状的二叉树。那么如果有不存在的叶节点,还能怎么表示吗?可以,但是我们当他不存在就是了。我们只要这颗线段树有这样的二叉树形状即可。
可以发现,任意一个节点的父节点都是孩子节点上二进制数右移一位得到,且为节点表示偶树时为左节点,反之为右节点。和线段树相同的,每一个节点维护了两个子节点的区间,所有的叶节点代表了一个点。
我们这里使用RMQ问题作为模板。
如何建树?
我们首先只能知道线段树中最多\(n\)个点。因此我们最多存在\(n\)个有效的叶子节点。我们只能知道叶子节点,因此我们是自底向上建树。
void build(ll n,ll &idx)
{
for(idx=1;idx<n;idx<<=1);
for(int i=idx<<1;i;--i)ranl[idx+i-1]=ranr[idx+i-1]=i;
for(int i=idx-1;i;--i)ranl[i]=ranl[ls(i)],ranr[i]=ranr[rs(i)];
}
我们需要解决RMQ问题,因此我们的\(pushup\)函数应该如此定义
void pushup(ll p){zkw[p]=max(zkw[ls(p)],zkw[rs(p)]);}
由于题目要求,我们需要动态开点
void add(ll x){ll i=idx+key;zkw[idx+(key++)]=x;while(i)i>>=1,pushup(i);}
如何维护信息
我们询问区间\([l,r]\)的最值。分类讨论:
①:当\(l=r\)时,根据定义,我们直接返回\(zkw[l]\)的值,即为答案。
②:当\(l\&1=0\)时,为二叉树中的左儿子,对于其父亲所管辖的区间,必然全包含\(l\)所管辖区间,因此我们可以放心的将\(l>>=1\),也就是让\(l\)访问父亲节点。
③:当\(l\&1=1\)时,为二叉树中的右儿子,明显,此时左儿子管辖的区间不应该加入更新,同时,如果将\(l\)直接访问父亲节点,会增加不该访问的区间。为了解决这个办法,我们可以记录\(l\)所维护的区间最值,并且\(++l\)。此时,\(l\)指向另一颗子树的左儿子,转操作②。
④:对于\(r\)来说同理,但是对于\(r\&0=1\)的情况,我们需要\(--r\)。
根据上述讨论,我们得到以下核心代码。
ll query(ll l,ll r)
{
ll res=0;
while(l!=r)
{
if(l&1)res=max(res,zkw[l++]);
if(r&0)res=max(res,zkw[r--]);
l>>=1,r>>=1;
}
return max(res,zkw[r]);
}
完善代码输入输出,得到最后的答案。
例题
$\large1275.最大数 $
#include<cstdio>
#include<cstring>
#include<bitset>
#include<algorithm>
#include<vector>
#include<iostream>
using namespace std;
typedef long long ll;
#define pb push_back
#define ls(i) (i<<1)
#define rs(i) (i<<1|1)
const int rg=2e5+7;
ll idx,n,p,key,dig,a,zkw[rg<<4],ranl[rg<<4],ranr[rg<<4];
char op[10];
void pushup(ll p){zkw[p]=max(zkw[ls(p)],zkw[rs(p)]);}
void build(ll n,ll &idx)
{
for(idx=1;idx<n;idx<<=1);
for(int i=idx<<1;i;--i)ranl[idx+i-1]=ranr[idx+i-1]=i;
for(int i=idx-1;i;--i)ranl[i]=ranl[ls(i)],ranr[i]=ranr[rs(i)];
}
void add(ll x){ll i=idx+key;zkw[idx+(key++)]=x;while(i)i>>=1,pushup(i);}
ll query(ll l,ll r)
{
ll res=0;
while(l!=r)
{
if(l&1)res=max(res,zkw[l++]);
if(r&0)res=max(res,zkw[r--]);
l>>=1,r>>=1;
}
return max(res,zkw[r]);
}
int main()
{
cin>>n>>p;
build(n,idx);
for(int i=1;i<=n;++i)
{
cin>>op>>dig;
if(op[0]=='A')add((dig+a)%p);
else a=query(idx+key-dig,idx+key-1),cout<<a<<'\n';
}
return 0;
}
区间修改
综上所述,ZKW线段树无论是时间,空间还是算法编写难度,都远远优于普通线段树,为什么没有推广使用呢?
可以发现,由于我们是通过自底向上建树,操作也是至底向上进行,导致我们的\(pushdown\)操作难以执行,区间修改问题具有一定的实现难度。
但是张昆玮本人提出了运用差分的思想进行区间修改维护,但是这样写下来,代码篇幅远长于普通线段树,此处不做介绍。
复杂度
时间复杂度:与普通线段树一样
空间复杂度:这里我们完全可以动态的给予内存,因此空间复杂度为\(O(n+2*第一个小于n的二次幂-1)\),也就是大多优于普通线段树
权值线段树+动态开点
权值线段树
之前我们学习的线段树维护矩形面积并,我们是以\(y\)轴为值域建立线段树,我们可以方便地处理平面内线段的重叠。
于是我们将这种思想推广,得到了一个独特的名称——权值线段树。
试想,我们需要在一个给定的序列内求第\(K\)大值,并且存在一个操作,使得其中一个已经存在值域内的数于任意位置增加(减少)\(p\)个,如何快速求得?
方法一:暴力,复杂度过高,不考虑。
方法二:排序,找值,由于插入数的次数可能会很多,复杂度过高,不考虑。
方法三:建立对顶堆,找第\(K\)大。似乎可以在\(O(n*\log n)\)的时间内完美的处理,但是由于插入的数的数量可能会很多,导致时间复杂度过高,不考虑。
...还有很多很多方法,此后的文章会涉及,上面只是给出最简单的解法。
很容易的我们可以这样想,我们不要求区间询问的话,我们可以以值域建立一颗二叉树。
可以发现,这个不是和线段树一模一样吗?
我们每一个节点维护了值域\([l,r]\)中出现了\(n\)个数字,叶节点维护了值域中第\(l\)种数出现了\(n\)次。
思想和线段树一模一样,每一个节点管辖左右儿子管辖的区间。
如果我们要找第\(K\)大,我们从根节点开始搜索,如果左儿子管辖区间的数大于\(K\),那么答案一定在左儿子内。
右儿子同理。依次类推,我们可以找到叶节点,也就是答案。
讲完了?讲完了。
例题
\(\large P1801 黑匣子\)
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
const int rg=2e5+7;
struct segtree{int val;}seg[rg<<2];
int a[rg],b[rg],c[rg],u[rg],val[rg<<2],ls[rg<<2],rs[rg<<2],pos[rg<<2],cnt,tot;
int find(int x){return lower_bound(c+1,c+tot+1,x)-c;}
void pushup(int p){seg[p].val=seg[ls[p]].val+seg[rs[p]].val;}
void modify(int x,int k,int &p,int l,int r)
{
if(!p)p=++cnt,seg[p]={0};
if(l==r&&l==x){seg[p].val+=k;return;}
int mid=l+r>>1;
if(x<=mid)modify(x,k,ls[p],l,mid);
if(x>mid)modify(x,k,rs[p],mid+1,r);
pushup(p);
}
int query(int p,int k,int l,int r)
{
if(l==r)return c[l];
int mid=l+r>>1,nl=seg[ls[p]].val;
if(k<=nl)return query(ls[p],k,l,mid);
else return query(rs[p],k-nl,mid+1,r);
}
int main()
{
int n,p;
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>p;
for(int i=1;i<=n;++i)cin>>b[i],a[i]=b[i];
for(int i=1;i<=p;++i)cin>>u[i];
sort(a+1,a+n+1);
for(int i=1;i<=n;++i)
if(!tot||c[tot]!=a[i])c[++tot]=a[i];
for(int i=1,j=1;i<=n;++i)
{
modify(find(b[i]),1,pos[1],1,tot);
while(j<=p&&i>=u[j])cout<<query(pos[1],j,1,tot)<<'\n',++j;
}
return 0;
}
动态开点
我们刚刚看了上面那份代码,可能有人疑惑,你的\(build\)函数跑哪去了?对\(trie\)敏感的同学已经发现,它在这里。
void modify(int x,int k,int &p,int l,int r)
{
/*添加节点
if(!p)p=++cnt,seg[p]={0};
*/
if(l==r&&l==x){seg[p].val+=k;return;}
int mid=l+r>>1;
if(x<=mid)modify(x,k,ls[p],l,mid);
if(x>mid)modify(x,k,rs[p],mid+1,r);
pushup(p);
}
我们这里介绍动态开点的思想。
可以发现黑匣子那一题,我们的数是一个一个添加上去,刚开始我们是没有必要将整颗树建立完全,我们一个一个一个点的将数添加到叶节点当中,并且在这过程当中,我们一步步开辟新节点的存储空间。
要说它有什么用,也就是节省了存储空间,并且在后面我们提及的主席树中大有作为。
李超线段树
引入
这里有一个问题
①:支持在平面内插入一条直线
②:询问与直线\(x=a\)相交直线的最高\(y\)坐标
我们可以使用平衡时维护,我们维护每一个横坐标的最高直线
我们插入直线时,找到其插入斜率的前驱和后继,判断并删除,\(O(n\log n)\)内可以解决问题。
但是我们将题目改编
①:支持在平面内插入一条线段
②:询问与直线\(x=a\)相交线段的最高\(y\)坐标
我们发现普通的平衡树难以维护这样的信息,普通的线段树也难以维护,因为这样的懒标记下传是难以实现的。这里我们引入李超线段树。
线段树可以维护区间信息,因此我们维护平面的\(x\)轴。
根据以上的学习,我们的第一直觉就是建一颗线段树,每个叶节点存储其最高线段的信息。
那么问题来了,既然涉及了区间修改,我们怎么\(pushdown\)?
我们分类讨论:
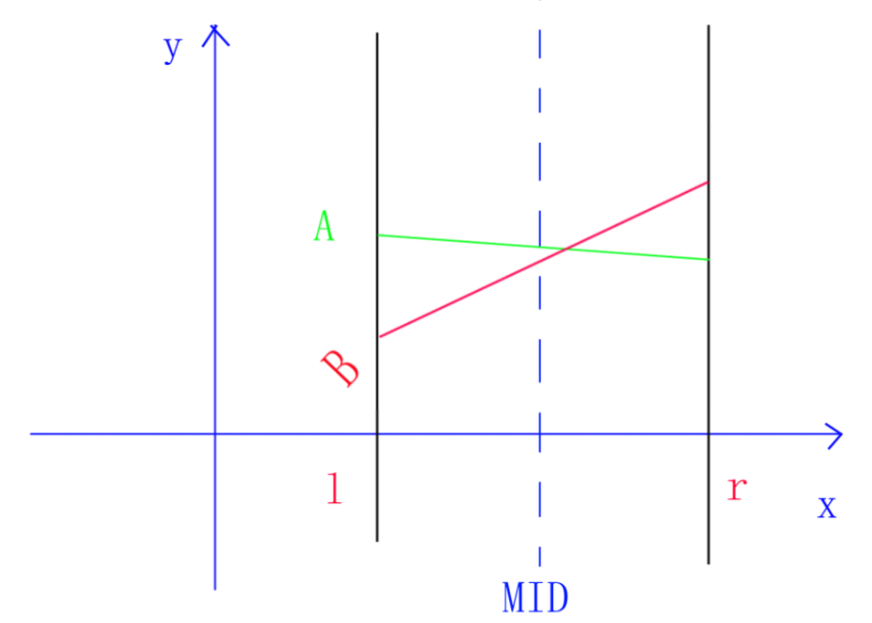
我们令新线段为B,旧线段为A。B覆盖区间\([l,r]\),则于区间\([l,r]\)内:
①:如果B完全覆盖A,则区间更新,将所有A替换为B,打上懒标记
②:如果A完全覆盖B,则直接\(return\)
③:如果B不完全覆盖A,则存在三种情况
(1)B在左半边全部优于A,但是对于右半边未知,因此我们给左半边打上懒标记,递归访问右半边情况,直至完全覆盖节点,并且这个过程中在各个节点打上懒标记。
(2)B在右半边全部优于A,但是对于左半边未知,因此我们给右半边打上懒标记,递归访问左半边情况,直至完全覆盖节点,并且这个过程中在各个节点打上懒标记。
(3)递归搜索B优于A的那半边
怎么一想,好像普通线段树的确能够维护。但是实际上当你去尝试,发现根本写不出来()
算法思想
对此,学军中学的李超在《省选讲课》提出了李超线段树的思想。
在区间\([l,r]\)中,$mid=\lfloor (l+r)/2\rfloor \(,存在直线A,B。如果\)y_{A}(mid)>y_{B}(mid)$。
则称\(A\)为区间\([l,r]\)的最优势线段。我们线段树维护其管辖区间的最优势线段。
我们记A为线段树上维护的旧线段,B为新线段。
插入线段
①:如果B完全覆盖A,则区间更新,将线段树维护的A替换为B,\(return\)
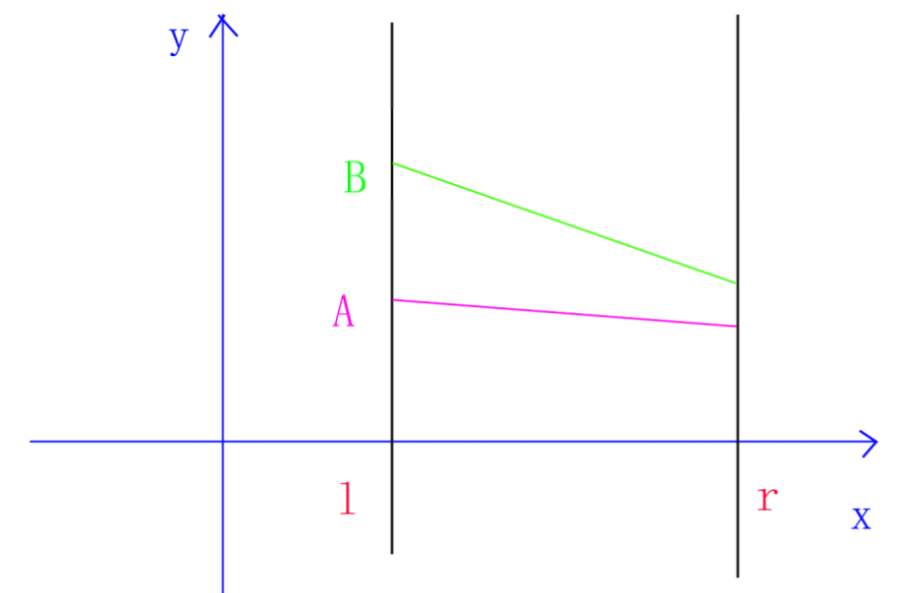
②:如果A完全覆盖B,则直接\(return\)
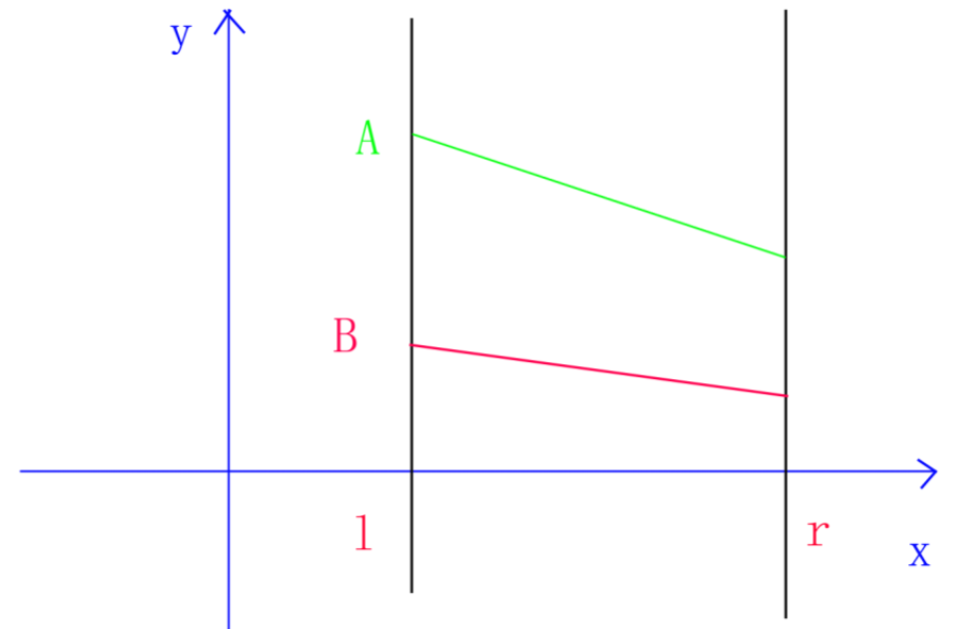
③:如果B不完全覆盖A,则存在两种情况
(1)\(y_{A}(mid)<y_{B}(mid)\),该区间的最优势线段修改为B,递归搜索B劣于A的那半边,此时将较劣的线段下传,也就是将B修改为A并且递归搜索。
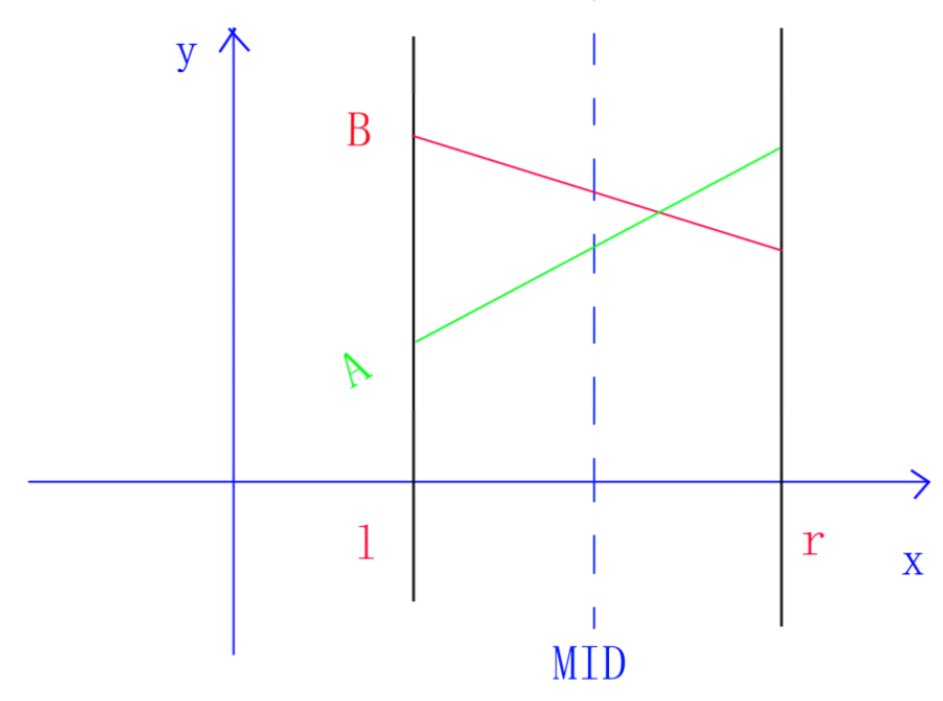
或
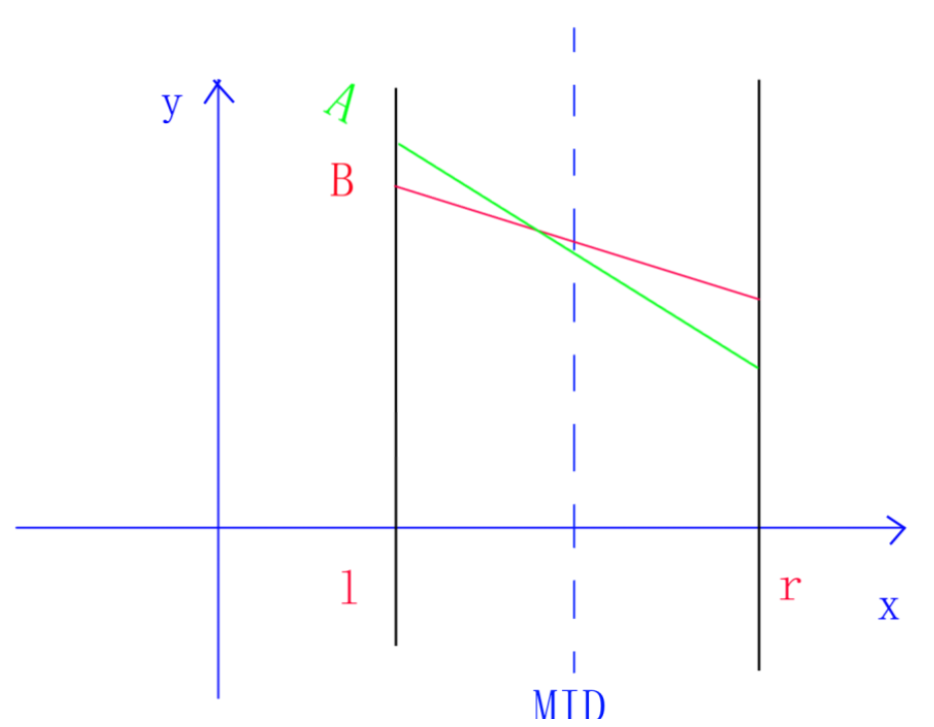
(2)\(y_{A}(mid)>y_{B}(mid)\),递归搜索B优于A的那半边。
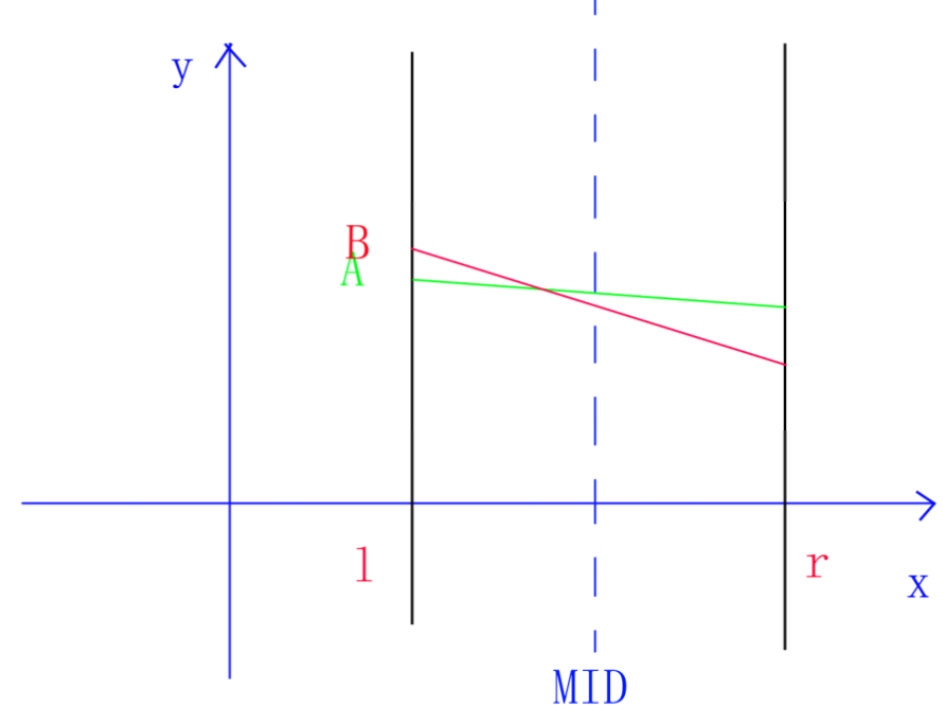
或
询问线段
因为我们维护每一个区间的最优势线段,我们不能一访问的线段就\(return\)。
我们只能按部就班的访问完毕整个路径取最大值。
记\([l,r]\)为当前区间,\(mid=\lfloor(l+r)/2\rfloor\)。
①:如果区间包含\(a\),求此时最优势线段在\(a\)处的\(y\),于历史值相比,求\(\max\),并且\(return \max\)
②:如果\(a<=mid\),\(return\) 递归搜索左半边
否则,\(return\) 递归搜索右半边
算法证明
我们查询直线\(x=a\)相交线段的最高\(y\)坐标\(\max\)。我们维护每一个区间\([l,r]\)的最优势线段,并且我们不能知道每一个区间维护的最优势线段于\(a\)的\(y\)是否为最高点,此处证明最高点因此存在维护的最优势线段中。
假设区间\([l,r]\)已经维护该区间的最优势线段A,\(mid=\lfloor(l+r)/2\rfloor\)。
分类讨论:
①:区间\([l,r]\)此前没有任何线段。因为此前无其余线段,因此也没有下放劣势线段,因此不存在儿子节点,故\(\max=y_{A}(a)\)。
②:区间\([l,r]\)此前存在\(k\)个线段且以区间\([l,r]\)为节点的子树有空。因为劣势线段被下放,我们向下访问,
因此能够访问到每一个经历\(x=a\)的线段\(B\),取\(\max=max(y_{B}(a))\)。
③:区间\([l,r]\)此前存在\(k\)个线段且以区间\([l,r]\)为节点的子树无空。存在一种情况,曾经于\(x=a\)有交的线段可能已经不在线段树当中维护。可以证明,其不影响答案准确性。只有当叶子节点被更新时,其维护的旧线段才会被删除,当为叶子节点时\(l=r=mid\),因此存在一个线段A优于线段树维护的最优势线段B时,A一定在整个区间都会高于B,\(y_{A}(a))>y_{B}(a))\),\(\max!=y_{B}(a)\)所以因此用A替代B不影响答案正确性。
证毕。
复杂度
插入线段时间复杂度\(O(n*\log^2 n)\),空间复杂度\(O(n)\)。
我们在插入操作不只线段树的搜索,还有区间以\(mid\)的分治,其近似区间长度\(\log\) 的复杂度,因此时间复杂度度最坏为\(O(n*\log^2 n)\),但是可以证明,还有区间以\(mid\)的分治产生的\(\log\)非常小,近似常数,可以\(1s\)跑\(1e5\)。
例题
\(\large P4097 [HEOI2013]Segment\)
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
const int rg=2e5+7,mod=39989,MOD=1e9,inf=0;
int ls[rg<<2],rs[rg<<2],rt[rg<<2],cnt,tot=1,t;
struct LCtree{int val;double k,b=-inf;}seg[rg<<2];
double get_y(double k,double b,int x){return k*x+b;}
double k_calc(int x,int y,int x1,int y1){return x!=x1?(double)(y1-y)/(x1-x):0;}
double b_calc(int x,int y,int x1,int y1){return x!=x1?y-(double)(y1-y)/(x1-x)*x:max(y,y1);}
void modify(int u,int v,double k,double b,int &p,int l,int r,int num)
{
if(!p)p=++cnt;
int mid=l+r>>1;
if(v<l||r<u)return;
if(u<=l&&v>=r)
{
double tk=seg[p].k,tb=seg[p].b;
if(l==r){if(get_y(k,b,l)>=get_y(tk,tb,l))seg[p]={num,k,b};return;}
if(k>tk&&b>tb)seg[p]={num,k,b};
else if(k>=tk)
{
if(get_y(k,b,mid)>get_y(tk,tb,mid))
modify(u,v,tk,tb,ls[p],l,mid,seg[p].val),seg[p]={num,k,b};
else modify(u,v,k,b,rs[p],mid+1,r,num);
}
else if(b>=tb)
{
if(get_y(k,b,mid)>get_y(tk,tb,mid))
modify(u,v,tk,tb,rs[p],mid+1,r,seg[p].val),seg[p]={num,k,b};
else modify(u,v,k,b,ls[p],l,mid,num);
}
return;
}
if(u<=mid)modify(u,v,k,b,ls[p],l,mid,num);
if(v>mid)modify(u,v,k,b,rs[p],mid+1,r,num);
}
void query(int p,int l,int r,int x,double &res,int &ans)
{
if(!p)return;
int mid=l+r>>1,t=seg[p].val;double k=seg[p].k,b=seg[p].b;
if(l==r)
{
if(res<get_y(k,b,x))res=get_y(k,b,x),ans=t;
return;
}
if(x<=mid)
{
if(res<get_y(k,b,x))res=get_y(k,b,x),ans=t;
query(ls[p],l,mid,x,res,ans);
}
else
{
if(res<get_y(k,b,x))res=get_y(k,b,x),ans=t;
query(rs[p],mid+1,r,x,res,ans);
}
}
int main()
{
int x,y,x1,y1,last=0,op;double h;
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
for(cin>>t;t;--t)
{
cin>>op;
if(!op)cin>>x,x=(x+last-1)%mod+1,query(1,1,mod,x,h=-inf,last=0),cout<<last<<'\n';
else
{
cin>>x>>y>>x1>>y1;
x=(x+last-1)%mod+1,x1=(x1+last-1)%mod+1;
y=(y+last-1)%MOD+1,y1=(y1+last-1)%MOD+1;
if(x1<x)swap(x1,x),swap(y1,y);
modify(x,x1,k_calc(x,y,x1,y1),b_calc(x,y,x1,y1),rt[1],1,mod,tot),++tot;
}
}
return 0;
}
主席树(可持久化线段树)
引入
我们这里引入一个问题:
给定长度为 \(N\) 的整数序列 \(A\),下标为 \(1∼N\)。现在要执行 \(M\) 次操作,其中第 \(i\) 次操作为给出三个整数 \(l_{i},r_{i},k_{i}\),求 \(A[l_{i}],A[l_{i+1}],…,A[r_{i}]\) (即 \(A\) 的下标区间 \([l_{i},r_{i}]\)中第 \(k_{i}\) 小的数是多少。
我们考虑对于整个区间而不是仅仅是区间\([l,r]\)内,求第\(K\)小。
做法就像为我们上面提到的权值线段树,我们可以在\(\log n\)的时间内求解。
但是这里给我们一个区间限制,相同的,我们考虑权值线段树的做法。
我们这里先给出一个公式
\(对于任意区间\)\([l,r],我们存在两个线段树A,B,分别维护区间[1,u],[1,v]。且u<=v\)
\(ls[p]代表p的左儿子,rs[p]代表p的右儿子,sum[p]代表p维护区间的数个数\)
\(按前缀和的思想,有公式:sum[区间[u,v]在值域[l,r]]=(sum[ls[B]在值域[l,r]]-sum[ls[A]在值域[l,r]])+(sum[rs[B]在值域[l,r]]-sum[rs[A]在值域[l,r]])\)
根据上述公式,我们求区间\([l,r]\)的第\(K\)小,就是按照\(v\)从\(1\)开始严格以\(1\)的增量建立管辖区间为\([1,v]\)的线段树,直至\(v>N\)。
按照这个想法,我们需要建立\(N\)颗线段树,大大的MLE+TLE打在脸上。
算法思想
这里有\(git\)的思想。就是每一次修改只依赖于上回的版本,我们的新版本从旧版本修正而来。我们使用新版本创建的规则创建,但是依赖于旧版本的模式。具体是在创建新版本时我们只遍历旧版本,将在遍历到的节点复制,将新版本的引出的指针指向该节点的拷贝,依次迭代。
这样,我们每次版本更新最多只增加\(\log n\)个节点,不必将整颗线段树建立。对于不同区间的线段树,我们只要访问不同的版本即可。
下面我们模拟上面的思路:
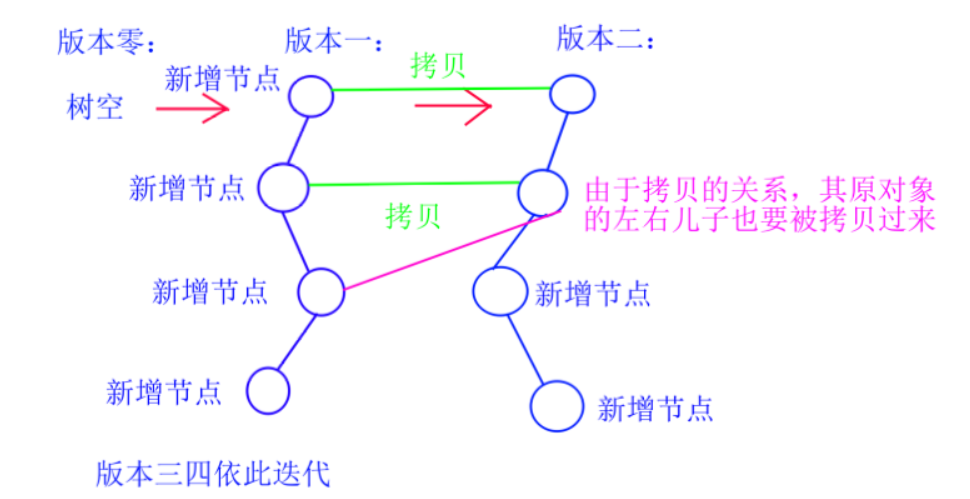
起初,我们只有区间\([1,1]\)的线段树,也就是版本\(1\),\(root[1]\)指向其根节点。我们现在要依靠某个规则创建版本\(2\),某个规则可能是添加某个值或者是些什么,在这个问题当中,如果我们添加了一个数,按照线段树搜索的思路,必然会改变且只改变最多\(\log n\)个区间,但是起初版本\(2\)是不存在的,因此我们只能按照其上的规则搜索版本\(1\)的某些节点。如果版本\(1\)存在节点我们就拷贝到版本\(2\)当中,否则我们只在版本\(2\)中创立新节点。如此迭代,直到所有版本的线段树被建立完毕。
我们发现,点并不是在更新线段树之前就建立完毕,而是一边更新版本,一边建立新节点,因此我们要使用动态开点的思想,建立新节点。
复杂度
时间复杂度:和普通线段树同理,一般在\(O(n*\log n)\)。
空间复杂度:应该不大于\(O(n*\log n+M*\log n)\),我们动态开点,每一次最多增加\(O(\log n)\)个节点数。
例题
\(\large P3834 【模板】可持久化线段树 2\)
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int rg=2e5+7;
struct gitsegtree{int val;}seg[rg*20];
int rt[rg],cnt,tot,ls[rg*20],rs[rg*20],a[rg],b[rg],c[rg];
int find(int x){return lower_bound(c+1,c+1+tot,x)-c;}
void pushup(int p){seg[p].val=seg[ls[p]].val+seg[rs[p]].val;}
void modify(int &u,int &fa,int l,int r,int x)
{
int mid=l+r>>1;
if(!fa)fa=++cnt;
u=++cnt;
seg[u]=seg[fa],ls[u]=ls[fa],rs[u]=rs[fa];
if(x<l||x>r||r<l)return;
if(l==r){++seg[u].val;return;}
if(x<=mid)modify(ls[u],ls[fa],l,mid,x);
else modify(rs[u],rs[fa],mid+1,r,x);
pushup(u);
}
int query(int u,int v,int l,int r,int k)
{
if(l==r)return c[l];
int mid=l+r>>1,dig=seg[ls[u]].val-seg[ls[v]].val;
if(k<=dig)return query(ls[u],ls[v],l,mid,k);
return query(rs[u],rs[v],mid+1,r,k-dig);
}
int main()
{
int n,p;
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>p;
for(int i=1;i<=n;++i)
cin>>a[i],b[i]=a[i];
sort(a+1,a+1+n);
for(int i=1;i<=n;++i)
if(!tot||c[tot]!=a[i])c[++tot]=a[i];
for(int i=1;i<=n;++i)
modify(rt[i],rt[i-1],1,tot,find(b[i]));rt[0]=0;
while(p--)
{
int l,r,k;
cin>>l>>r>>k;
cout<<query(rt[r],rt[l-1],1,tot,k)<<'\n';
}
return 0;
}
线段树合并
后面咕咕假期补上




