背包问题
我们考虑在一般试题当中出现的背包问题:
01背包问题
有 \(N\) 件物品和一个容量是 \(W\) 的背包。每件物品只能使用一次。
\(i\) 件物品的体积是 \(w_{i}\)价值是 \(v_{i}\)
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
0<\(N,W\)≤1000
0<\(v_{i},w_{i}\)≤1000
时间复杂度:\(O(N*W)\)
算法思想:我们对\(i\)个物品价值最大的选法进行分析,明显的,它必然从\(i-1\)个物品的组合中再任选不属于该\(i-1\)个物品的集合的一个物品叠加的价值的最大值。
我们设立一个二维数组\(f[i][j]\),其代表在\(i\)与\(j\)的条件下的最大价值,\(i\)代表选择了多少个物品,\(j\)代表已经占用背包的多少空间。
可以得到一个递推式:
\(if(j>=w[i])f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);\)
\(else\) \(f[i][j]=f[i-1][j];\)
也就是我们不重不漏的按顺序递推完成之后,最终\(f[n][W]\)得到的即为解。
int main() { int n,V; scanf("%d%d", &n, &W); for (int i = 1;i <= n;++i) scanf("%d%d", &v[i], &w[i]); for(int i=1;i<=n;++i) { for(int j=1;j<=W;++j) { if(j>=w[i])f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]); else f[i][j]=f[i-1][j]; } } printf("%d",f[n][W]); return 0; }可以发现,每一轮的递推均用上一轮的递推结果,即由\(f[i-1][?]\)向\(f[i][?]\)的递推。
因此我们可以做出空间上的优化。
此处我们按照\(W\)的逆序枚举就是为了保证\(f[i-1][?]\)向\(f[i][?]\)的递推。
int main() { int n,V; scanf("%d%d", &n, &W); for (int i = 1;i <= n;++i) scanf("%d%d", &v[i], &w[i]); for(int i=1;i<=n;++i) for(int j=W;j>=w[i];++j) f[j]=max(f[j],f[j-w[i]]+v[i]); printf("%d",f[W]); return 0; }
完全背包问题
有 \(N\) 件物品和一个容量是 \(W\) 的背包。每件物品能使用无限次。
\(i\) 件物品的体积是 \(w_{i}\)价值是 \(v_{i}\)
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
0<\(N,W\)≤1000
0<\(v_{i},w_{i}\)≤1000
我们不考虑贪心做法,我们直接考虑动态规划做法。
时间复杂度:\(O(N*W)\)
算法思想同01背包问题,但是注意每个物品能选无限件,也就是我们不能简单的从\(f[i-1][?]\)向\(f[i][?]\)的递推,我们还要考虑\(f[i][?]\)向\(f[i][?]\)的递推。但是代码写起来明快了很多。
此处我们按照\(W\)的顺序枚举就是即为了保证\(f[i-1][?]\)向\(f[i][?]\)的递推,又为了保证\(f[i][?]\)向\(f[i][?]\)的递推。
int main() { int n,W; scanf("%d%d", &n, &W); for (int i = 1;i <= n;++i) scanf("%d%d", &w[i], &v[i]); for(int i=1;i<=n;++i) for(int j=w[i];j<=W;++j) f[j]=max(f[j],f[j-w[i]]+v[i]); printf("%d",f[W]); return 0; }
多重背包问题
有 \(N\) 件物品和一个容量是 \(W\) 的背包。每件物品最多能使用\(s_{i}\)次。
\(i\) 件物品的体积是 \(w_{i}\)价值是 \(v_{i}\)
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
0<\(N,W\)≤100
0<\(v_{i},w_{i},s_{i}\)≤100
时间复杂度:\(O(N*W*\sum_{i=1}^{N}s[i])\)
这里我们只是相较于01背包问题多了一层\(s[i]\)即物品件数的考虑,没什么特别的。
int main() { int n,W; scanf("%d%d", &n, &W); for (int i = 1;i <= n;++i) scanf("%d%d%d", &w[i], &v[i],&s[i]); for(int i=1;i<=n;++i) for(int j=W;j>=1;--j) for(int k=0;k<=s[i];++k) if(k*w[i]<=j)f[j]=max(f[j],f[j-k*w[i]]+k*v[i]); printf("%d",f[W]); return 0; }
多重背包问题____二进制优化
有 \(N\) 件物品和一个容量是 \(W\) 的背包。每件物品最多能使用\(s_{i}\)次。
\(i\) 件物品的体积是 \(w_{i}\)价值是 \(v_{i}\)
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
0<\(N\)≤1000
0<\(V\)≤2000
0<\(v_{i},w_{i},s_{i}\)≤2000
我们可以发现,多重背包问题下,时间复杂度过高,因此我们考虑优化。
显然的,对于任意一个数字,我们都可以将它拆分为\(2^0+2^1+...+2^n\)的形式。
(注意,与二进制形式的幂次不同,这里只是按严格递增幂次的顺序拆分)
同理的,对于一种价值为\(v\)的物品,总共存在\(s\)件。我们可以将其\(s\)拆分为其上的组合。
因此我们将\(s\)件的物品最多拆分为\(\log s\)件物品。
在递推的枚举当中,必然会不重不漏的经历每一种状态。
但是我们去最大值的原因,不少价值小的状态未加入计算,减少了时间复杂度。
同理的,我们可以举一反三,进行三进制拆分等,理论时间复杂度均等,全看数据。例如这题八进制拆分能够得到最快的运行结果。
#include<cstdio> #include<iostream> #include<algorithm> #define pb push_back using namespace std; int s,f[1000007],n,W; vector<int>w,v; int main() { int num[15]={1,2,4,8,16,32,64,128,256,512,1024,2048,5096,10192}; cin>>n>>W; for(int i=1;i<=n;++i) { int vv,ww; cin>>ww>>vv>>s; for(int k=0;k<14&&num[k]<=s;++k) w.pb(num[k]*ww),v.pb(num[k]*vv),s-=num[k]; if(s)w.pb(s*ww),v.pb(s*vv); } for(int i=0;i<w.size();++i) for(int j=W;j>=w[i];--j) f[j]=max(f[j],f[j-w[i]]+v[i]); cout<<f[W]; return 0; }
多重背包问题____单调队列优化
有 \(N\) 件物品和一个容量是 \(W\) 的背包。每件物品最多能使用\(s_{i}\)次。
\(i\) 件物品的体积是 \(w_{i}\)价值是 \(v_{i}\)
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
0<\(N\)≤1000
0<\(V\)≤20000
0<\(v_{i},w_{i},s_{i}\)≤20000
我们对\(f[i][j]\)进行空间优化,现在,对于任意一个\(f[j]\)怎样由其余数据递推?
我们令 \(f[j]\) 表示容量为\(j\)的情况下,获得的最大价值
那么,针对每一类物品\(i\) ,我们都更新一下 \(f[m] --> f[0]\) 的值,最后 \(f[m]\) 就是一个全局最优值\(f[m] = max(f[m], f[m-v] + w, f[m-2*v] + 2*w, f[m-3*v] + 3*w, ...)\)
接下来,我们把 \(f[0] --> f[m]\) 写成下面这种形式
\(f[0], f[v], f[2*v], f[3*v], ... , f[k*v]\)
\(f[1], f[v+1], f[2*v+1], f[3*v+1], ... , f[k*v+1]\)
\(f[2], f[v+2], f[2*v+2], f[3*v+2], ... , f[k*v+2]\)
...
\(f[j], f[v+j], f[2*v+j], f[3*v+j], ... , f[k*v+j]\)
显而易见,\(m\) 一定等于 \(k*v + j\),其中 \(0 <= j < v\)
所以,我们可以把 \(f\) 数组分成 \(j\) 个类,每一类中的值,都是在同类之间转换得到的
也就是说,\(f[k*v+j]\) 只依赖于{\(f[j], f[v+j], f[2*v+j], f[3*v+j], ... , f[k*v+j]\)}
因为我们需要的是{\(f[j], f[v+j], f[2*v+j], f[3*v+j], ... , f[k*v+j]\)}中的最大值。
可以通过维护一个单调队列来得到结果。这样的话,问题就变成了 \(j\) 个单调队列的问题
很显然,找最大的值,因此我们可以考虑使用单调队列优化。
单调队列此处不做介绍时间复杂度:\(O(N*W)\)
int f[rg],q[rg],g[rg]; int main() { int n,m,v,w,s; scanf("%d%d",&n,&m); for(int i=1;i<=n;++i) scanf("%d%d%d",&v,&w,&s), obj[i]={w,v,s}; for(int i=1;i<=n;++i) { memcpy(g,f,sizeof f); for(int j=0;j<obj[i].v;++j) { int l=0,r=-1; for(int k=j;k<=m;k+=obj[i].v) { while(r>=l&&k-q[l]>obj[i].s*obj[i].v)++l; while(r>=l&&g[k]-(k-j)/obj[i].v*obj[i].w>=g[q[r]]-(q[r]-j)/obj[i].v*obj[i].w)--r; q[++r]=k; f[k]=max(f[k],g[q[l]]+(k-q[l])/obj[i].v*obj[i].w); } } } printf("%d",f[m]); return 0; }
有依赖的背包问题(树上背包问题)
有 \(N\) 个物品和一个容量是 \(V\) 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
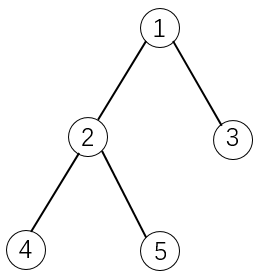
如下图所示:
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是 \(i\),体积是 \(v_{i}\),价值是 \(w_{i}\),依赖的父节点编号是 \(p_{i}\)。物品的下标范围是 \(1…N\)。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
0<\(N,W\)≤100
0<\(v_{i},w_{i}\)≤100
根节点\(p=-1\)
依照01背包的思路,我们可以写出,由于其依赖于根是否被选取,因此会有些差异。
struct node {int c,w;}box[maxn]; struct edge {int u,v,ne;}e[maxn]; int head[maxn],cnt,f[107][10007]; void add(int u,int v){e[++cnt]={u,v,head[u]},head[u]=cnt;} void dfs(int root,int tot) { if(root==-1)return; for(int i=box[root].c;i<=tot;++i)f[root][i]=box[root].w;//父节点必选 for(int i=head[root];i!=-1;i=e[i].ne) { int v=e[i].v; dfs(v,tot); for(int j=tot;j>=box[root].c;--j) { for(int k=j-box[root].c;k>=0;--k) f[root][j]=max(f[root][j],f[root][j-k]+f[v][k]); } } } int main() { int n,V,fa,root; memset(head,-1,sizeof head); scanf("%d%d",&n,&V); for(int i=1;i<=n;++i) { scanf("%d%d%d",&box[i].c,&box[i].w,&fa); if(fa==-1)root=i; else add(fa,i); } dfs(root,V); printf("%d",f[root][V]); return 0; }
⑦:巨大背包问题(依赖于数量的背包问题)
1<=\(N\)<=40
\(w_{i},v_{i},W\)均可视为无限大。
为了方便表示我们约定
\(w_{i},v_{i},W\)<\(10^{15}\)
二分搜索+状态压缩
这里如果使用动态规划的方法,无论时间还是空间均会超出限制。
因此我们只能考虑最平凡的解法——搜索。
但是一般的搜索又会超出时间限制,因此我们考虑优化。
我们将左半边整理,对于左半边的任意组合价值与重量我们存储到表中。
我们再定义一个合适的偏序,将表中的数据排好序。
对于右半边的所有组合,我们均在左半边组成的顺序表中寻找最优解,即最大合法解。
我们考虑二分查找,因此优化至\(\log\)。
时间复杂度:\(O(\frac{n}{2}*2^{\frac{n}{2}}*\log2^{\frac{n}{2}})\)
#include<cstdio> #include<cstring> #include<vector> #include<cmath> #include<bitset> #include<algorithm> #include<iostream> #define fi first #define se second using namespace std; typedef long long ull; const ull inf=1e18; pair<ull,ull>lft[1<<23],e[155]; int main() { int n; ull m,maxx=0; cin>>n>>m; for(int i=0;i<n;++i) cin>>e[i].se>>e[i].fi; int llim=n/2,rlim=n-llim; for(int i=0;i<1<<llim;++i) { ull tot=0,vov=0; for(int j=0;j<llim;++j) if((i>>j)&1)tot+=e[j].fi,vov+=e[j].se; lft[i]={tot,vov}; } sort(lft,lft+(1<<llim)); int r=0; for(int i=0;i<(1<<llim);++i) if(lft[r].se<lft[i].se)lft[++r]=lft[i]; for(int i=0;i<1<<rlim;++i) { ull tot=0,vov=0; for(int j=0;j<rlim;++j) if((i>>j)&1)tot+=e[j+llim].fi,vov+=e[j+llim].se; if(tot<=m) { ull k=(upper_bound(lft,lft+r+1,make_pair(m-tot,inf))-1)->se; maxx=max(maxx,vov+k); } } cout<<maxx; return 0; }