算法竞赛进阶指南_打卡_题解_0x10

①：蚯蚓：队列，推公式
https://www.acwing.com/problem/content/135/

蛐蛐国里现在共有 n 只蚯蚓，第 i 只蚯蚓的长度为 ai ，所有蚯蚓的长度都是非负整数，即可能存在长度为 0 的蚯蚓。
每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只，将其切成两段。
若有多只最长的，则任选一只。
神刀手切开蚯蚓的位置由有理数 p 决定。
一只长度为 x 的蚯蚓会被切成两只长度分别为 \(⌊px⌋\) 和 \(x−⌊px⌋\) 的蚯蚓。
特殊地，如果这两个数的其中一个等于 0，则这个长度为 0 的蚯蚓也会被保留。
此外，除了刚刚产生的两只新蚯蚓，其余蚯蚓的长度都会增加一个非负整数 q。
蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是救兵还需要 m 秒才能到来。
蛐蛐国王希望知道这 m 秒内的战况。
输入格式
第一行包含六个整数 \(n,m,q,u,v,t\)，其中：\(n,m,q\) 的意义参考题目描述；\(u,v,t\) 均为正整数；你需要自己计算 \(p=u/v\)（保证 \(0<u<v\)）；\(t\) 是输出参数，其含义将会在输出格式中解释。
第二行包含 \(n\) 个非负整数，为 \(a_{1},a_{2},…,a_{n}\)，即初始时 \(n\) 只蚯蚓的长度。
同一行中相邻的两个数之间，恰好用一个空格隔开。
输出格式
第一行输出 \(⌊m/t⌋\) 个整数，按时间顺序，依次输出第 \(t\) 秒，第 \(2t\) 秒，第 \(3t\) 秒，……被切断蚯蚓（在被切断前）的长度。
第二行输出 \(⌊(n+m)/t⌋\) 个整数，输出 \(m\) 秒后蚯蚓的长度；需要按从大到小的顺序，依次输出排名第 t，第
\(2t\)，第 \(3t\)，……的长度。
\(1≤n≤10^5, 0≤ai≤10^8, 0<p<1, 0≤q≤200, 0≤m≤7∗10^6, 0<u<v≤10^9, 1≤t≤71\)

题目挺长的，我们通读一遍题目，就可以知道我们需要维护一个序列\(X\)，并且序列\(X\)能够做以下操作

①将最大的值分为\(⌊px⌋\) 和 \(x−⌊px⌋\)两个值
②对于其他未操作的值，我们均加上\(q\).

我们可以这么想，对于每一个值我们放入一个优先队列中，我们每次取最大值，分解为两个小值放入优先队列中，重复\(m\)次即可求出答案。对于其余数的变化如何操作呢，我们只要在插入值时减去\(q\)，又在最后对每一个值加上\(m*q\)即可。
时间复杂度为\(O(m\log_2x)\)
但是！！！！！
这个题目的数据范围实在是太大了，尤其是\(m\)，利用优先队列会炸的。
我们通过上述加数的过程进行了优化，我们现在考虑对于寻找每一个最大值的优化，使其复杂度不依赖于\(m\)。
以下就是神仙才想出来的推公式：我不会，我爬
我们记每一个值所分出来的小值为\(l\)，大值为\(r\)。

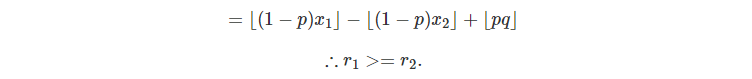
上面公式就是说，每一次分得的值一定比之前分得的值小，无论大值还是小值。
因此即使我们利用普通的队列来存也能够保证单调下降，并且\(q.front()\)即为最大值。
拥有上述推导后，我们即可在\(O(m+n\log_2n)\)的时间内得出答案。




②：最长异或值路径：字典树，贪心
https://www.acwing.com/problem/content/description/146/

给定一个树，树上的边都具有权值。
树中一条路径的异或长度被定义为路径上所有边的权值的异或和
⊕ 为异或符号。
给定上述的具有 n 个节点的树，你能找到异或长度最大的路径吗？

这道题和我以前写过的 最大异或对 特别像。
不过这里我们需要推出一个公式。

假设我们的树存在一个根节点。我们记从根节点到树上任意一点\(v\)的路径异或值为\(d[v]\)。
因此对于任意两个点\(u,v\)之间路径的异或值必然为\(d[u]⊕d[v]\)。（仔细一想就能想通，因为\(k⊕k==0\)）
并且无论取谁为根，均不会影响答案。

因此我们的问题已经完全转化为求\(d[0...n-1]\)两对数之间的最大异或数对。
对于每一个\(d[i]\)如何求其对应的最大异或数对?

我们只要找每一个对应二进制位数尽量相反（位数从高到低选取），就能保证有最大异或值。
如果我们找n个数的任意两个数最大的异或值，最坏只有O（n*32）;

③：雪花雪花雪花：hash，最小表示法
https://www.acwing.com/problem/content/description/139/

有 N 片雪花，每片雪花由六个角组成，每个角都有长度。
第 i 片雪花六个角的长度从某个角开始顺时针依次记为 ai,1,ai,2,…,ai,6。
因为雪花的形状是封闭的环形，所以从任何一个角开始顺时针或逆时针往后记录长度，得到的六元组都代表形状相同的雪花。
例如 ai,1,ai,2,…,ai,6 和 ai,2,ai,3,…,ai,6，ai,1 就是形状相同的雪花。
ai,1,ai,2,…,ai,6 和 ai,6,ai,5,…,ai,1 也是形状相同的雪花。
我们称两片雪花形状相同，当且仅当它们各自从某一角开始顺时针或逆时针记录长度，能得到两个相同的六元组。
求这 N 片雪花中是否存在两片形状相同的雪花
\(1≤N≤100000 , 0≤ai,j<10000000\)

因为我不懂蓝书上面“任意取一个hash函数即可”，这个条件，我就按照最小表示法来解题了。
由题意可知，雪花为环形，我们可以利用双倍长度的原雪花处理。
我们对每个雪花求最小表示。（注意，最小表示对其正反各求一次，取最小的为最小表示法，因为雪花既可以顺时针有可以逆时针转）
然后如果存在两个相同的最小表示
什么是最小表示？

对于一个字符串，我们可以将其最后一位提到第一位，其余位往后移一格。如此循环，所得的最小字典序的字符串为最小表示。

如何求最小表示？

暴力O(n^2)模拟
目前位置，我们已经对原字符串S延长为原来的两倍。
我们设立指针\(l,r\)。分别代表以其作为开始字符的下标位置。
很显然如果\(S[l]==S[r]\)则无法判断其对应开头的字典序大小，因此我们设立指针\(k\)，记为\(l,r\)共享的偏移量。
如果有\(S[l+k]>S[r+k]\)，因为在\(S[l...l+k-1]\)的字符均与\(S[r...r+k-1]\)相同，因此答案不可能存在\(l...l+k-1\)或\(r...r+k-1\)内。
因为\(S[l+k]>S[r+k]\)答案亦不存与\(l+k\)上。
因为我们求最小表示法我们因此使\(l\)转变为\(l+k+1\)。
如果转变后出现了状态\(l==r\)我们继续判断是没有意义的，因为无论k值如何均有\(S[l+k]==S[r+k]\)，在这时我们令\(l++\)即可。
对于\(S[l+k]<S[r+k]\)同理。
最后我们求出的的\(l\)与\(r\)其实会对应改变后字符串的同一字符，不过我们使原字符串的长度加倍，因此我们指向原字符串的最小表示法下标为\(min(l,r)\)

佬门看一下hash怎么做呗，任取一个hash函数给我整不会了。




④：序列：堆，推公式
https://www.acwing.com/problem/content/148/
又是一道我八会的题。

给定 m 个序列，每个包含 n 个非负整数。
现在我们可以从每个序列中选择一个数字以形成具有 m 个整数的序列。
很明显，我们一共可以得到 \(n^m\) 个这种序列，然后我们可以计算每个序列中的数字之和，并得到 nm 个值。
现在请你求出这些序列和之中最小的 n 个值。
\(0<m≤1000, 0<n≤2000\)

我们首先对于两个序列a,b，若a均排完序，必然可得的\(min(a[1]+b[1],...,a[1]+b[n])\)为最小和值。
当我们选取a[1]+b[l]为最小和值时，对于第二小和值，则一定会将a[2]+b[l]考虑进去。
则第二小和值为\(min(a[1]+b[1],...(expect(a[1]+b[l])),a[2]+b[l],...,a[1]+b[n])\)
以此类推。
意思也就是我们将每一个a[i]+b[j]看做第k小时，第k+1小一定会考虑a[i+1]+b[j]。
本题我们可以维护一个堆，存储\(a[1]+b[1],...(expect(a[1]+b[l])),a[2]+b[l],...,a[1]+b[n]\)。
每一轮寻找直至当前位置前n小值与新列值的前n小和值，重复n轮，即可求出结果。




⑤：双栈排序：栈，二分图，贪心
https://www.acwing.com/problem/content/155/

Tom 最近在研究一个有趣的排序问题。
通过 2 个栈 S1 和 S2，Tom 希望借助以下 4 种操作实现将输入序列升序排序。
操作 a
如果输入序列不为空，将第一个元素压入栈 S1
操作 b
如果栈 S1 不为空，将 S1 栈顶元素弹出至输出序列
操作 c
如果输入序列不为空，将第一个元素压入栈 S2
操作 d
如果栈 S2 不为空，将 S2 栈顶元素弹出至输出序列
如果一个 1∼n 的排列 P 可以通过一系列操作使得输出序列为 1,2,…,(n−1),n，Tom 就称 P 是一个”可双栈排序排列”。
Tom 希望知道其中字典序最小的操作序列是什么
\(1≤n≤1000\)

我第一眼看到这个东西就模拟去了（）
直到看到题解才发现妙死人的解法。
浏览题面，我们必然可以想出维护最小与次小值来维护答案，控制字典序最小。
具体怎么做

因为我们想要字典序最小，因此我们无脑将最先开始的a中元素元素放入栈s1中，记r为a数组的右指针。
当\(a[r]==k\)，k为未入输出序列的元素最小值，s1.push(a[r]),s1.pop(),++r。
当\(s1.top()==k+1\)并且序列中元素无k，则另起s2存储直至\(a[r]==k\)为止。

我们可以发现一个性质

如果s1或s2不是单调递减，则一定无解。
为什么，因为如果当\(j>i\)且\(s1[i]<s[j]\)时只有i先比j被弹出，才能得到一个合法序列，可是因为\(j>i\)则说明j一定会比i先弹出。因此无解。

因此我们需要关注的信息就是在大小为k值出栈前的情况下，s1可容忍的最大值为多少。
设 \(f[x[i]]\) 表示 \(x[i]\) 出栈前最大的数

则 \(f[x[i]]=f[x[i]−1]\)
若 x[i] - 1 出现的位置在 x[i] 之后 j 那么

\(f[x]=max(f[x],max(f[x[i+1 ... j−1]],x[i+1 ... j−1]))\)
我们s1的每一个放入的值c与可容忍的最大值f[c]，我们就可以尽可能的使字典序最小。
（蛮难的所实话）




⑥：奶牛矩阵：KMP
https://www.acwing.com/problem/content/description/161/

现在在每个奶牛的身上标注表示其品种的大写字母，则所有奶牛共同构成了一个 R 行 C 列的字符矩阵。
现在给定由所有奶牛构成的矩阵，求它的最小覆盖子矩阵的面积是多少。
如果一个子矩阵无限复制扩张之后得到的矩阵能包含原来的矩阵，则称该子矩阵为覆盖子矩阵。
\(1≤R≤10000, 1≤C≤75\)

这道题浏览过后第一反应就是求循环节有关，自然会想到KMP。

我们从奶牛矩阵的点（1,1）开始，我们首先对每一行分析：
如果第i行的最小循环节为k则此后行要求满足的循环节长度必须大于k,否则不能构成覆盖子矩阵。

现在我们考虑相邻两行的循环节k,p导致的覆盖子矩阵行上宽度大小变化：
①：若k==p,覆盖子矩阵的宽度无变化。
②：若k!=p，我们的第一反应是求最小公倍数，确实是没有正确性的。例如：aaaabaa aaaabac
当我们确定两行的最小循环节时，更大的循环节可能会成为更优解。
综上所述，我们只能暴力枚举行最小循环节长度
应该还有其他性质导致不能行上KMP，有无大兄弟证明一下

现在，我们枚举出了行最小循环节，现在我们只要KMP出列最小循环节即可。
res=行最小*列最小。




⑦：匹配统计：KMP，后缀和，差分呜呜好难
https://www.acwing.com/problem/content/162/

在每个问题中，他给定你一个整数 x，请你告诉他有多少个位置，满足“字符串 A 从该位置开始的后缀子串”与 B 匹配的长度恰好为 x。
例如：A=aabcde，B=ab，则 A 有 aabcde、abcde、bcde、cde、de、e 这 6 个后缀子串，它们与 B=ab 的匹配长度分别是 1、2、0、0、0、0。
因此 A 有 4 个位置与 B 的匹配长度恰好为 0，有 1 个位置的匹配长度恰好为 1，有 1 个位置的匹配长度恰好为 2。
\(1≤N,M,Q,x≤200000\)

看到前后缀匹配，我们自然会想到KMP，但是KMP求出的ne[i]数组的含义为以第i为结尾的最大相同前后缀长度。
可是题目要以A的每一个位置可是做前缀，但KMP只能做后缀。
我们知道KMP中求KMP数组及模式串与匹配串匹配时ne[i]=j的含义，因此可以知道j为匹配位数。
ne[i]=j，因此i-j+1位置上能匹配j位，当匹配继续进行后，当i-j+1位置再次匹配必然比上一次还要大。
也就是i-j+1位置的最大后缀匹配会被更新，因此我们不能统计每个值一共出现了多少次，我们只能知道大于等于某个值出现了多少次。
当指针i继续向后移时，其前每个位置的最大匹配可能会发生变化，并且j只更新最大的匹配，不能确保每一个匹配都会被更新，因此\(maxx[i-j+1]=max(maxx[i-j+1],j)\)被×掉了。
因此我们可以利用差分的思想，记cnt[k]为大于等于k的最大匹配数，则答案为cnt[k]-cnt[k+1]。
又因为ne[i]=j的关系，每当第i+j-1位加上某个值时，第j为也要同时加上。
我们就有一个公式\(cnt[ne[i]]+=cnt[i]\)。

对于cnt[ne[ne[i]]]怎么办？
因为ne[i]<=i，我们只要倒序枚举i当i=ne[i]时此时ne[i]=ne[ne[i]]。保证了正确性。

我们就可以求出大于等于某个值的后缀和了。
接下来cnt[k]-cnt[k+1]就能求出res。




⑧：矩阵：二维哈希，字符串哈希
https://www.acwing.com/problem/content/158/

给定一个 M 行 N 列的 01 矩阵（只包含数字 0 或 1 的矩阵），再执行 Q 次询问，每次询问给出一个 A 行 B 列的 01 矩阵，求该矩阵是否在原矩阵中出现过。\(A≤100 ，M,N,B≤1000，Q≤1000\)

我们考虑一维情况，在字符串A中怎么确定其中存在字符串b。在不考虑KMP下，我们考虑字符串哈希。
现在我们将情况推广到二维情况。我们可以求矩阵字符串的哈希值，然后\(O(1)\)查询即可。

如何求矩阵字符串的哈希值？
我们记哈希值数组为\(h\)，记字符串为\(s\)，二维从第一行开始以第i行为结尾且宽度为b的矩阵哈希值为res[i]，pw为任意一个大质数，p[i]等价于\(p^i\)。
对于一维字符串，存在公式：\(h[i]=h[i-1]*pw+s[i]-'0'\)
在二维，我们就可以有，\(res[i]=res[i-1]*p[b]+\sum_{l}^{l+b-1}h\)

题目要求我们计算\(a*b\)大小的矩阵哈希值考虑到我们开res[maxn][maxn][maxn]肯定是不够的。
因此我们只用一个变量代表以坐标（i,j）为结尾且大小为\(a*b\)的矩阵哈希值。
我们枚举行数，枚举列数，计算哈希值。
复杂度\(O(n*m*a*b)\)，很明显，复杂度爆了。我们考虑预处理。
因为存在公式\(\sum_{l}^{l+b-1}h\)我们考虑使用前缀和预处理每一行的哈希值。
因为从第b列开始，才能符合存在\(a*b\)子矩阵的性质。
我们对每一行做哈希求和，当行数大于等于a时，才为\(a*b\)的子矩阵，因此我们可以将其哈希值加入散列表中。
当行数大于a时，我们就要考虑将res减去第一行的哈希值。如此迭代，将res哈希值控制在\(a*b\)的子矩阵内。
对于每一个询问，我们将其询问的矩阵哈希值算出，在散列表中查询。
复杂度\(O(q*a*b+n*m)\).
\(******\)
现在讲讲我开始的错误做法。
首先，我们哈希，这是大家都认同的。
但是，我想像前缀和一样\(O(1)\)是时间内求出\(n*m\)矩阵的每一个\(a*b\)子矩阵的哈希值。
于是在我们求出矩阵哈希便有公式：
row[i][j]为第i行直至第j个字符的哈希值。pre[i][j]便为
\(row[i][j]+=row[i][j-1]*pw+mp[i][j]-'0';\)
\(pre[i][j]=pre[i-1][j]+row[i][j]*p[i];\)
但是如果这样处理，对于每一个我要加入散列表的\(a*b\)矩阵就要除以一个\(p[i-1]*p[j-1]\)
由于爆ull，所以不符合可除性
因此就错了。




⑨：树形地铁系统：树的最小表示。
https://www.acwing.com/problem/content/159/

你从中央车站出发，随机选择一条地铁线，然后乘坐地铁行进。
每次到达一个车站，你都将选择一条尚未乘坐过的地铁线路进行乘坐。
如果不存在未乘坐过的线路，则退回到上一个车站，再做选择。
直到你将所有地铁线路都乘坐过两次（往返各一次），此时你将回到中央车站。
之后，你以一种特殊的方式回忆自己的坐车过程，你将你的完整地铁乘坐路线编码为一个二进制字符串。
其中 0 编码表示你乘坐地铁线路到达距离中央车站更远的一站，1 编码表示你乘坐地铁线路到达距离中央车站更近的一站。
对于每个测试用例，如果两个字符串描述的探索路线可以视为同一个地铁系统的两种探索路线，则输出 same。

否则，输出 different。

对于每一个零一串，我们考虑是否存在一个唯一的表示方法。我们首先会考虑01字符串的最小字符串表示。

如何求树上的最小表示？
我们可以发现，存在一个性质，一个0必然会对应一个1，并且两个对应的01字符对应之间的01字符串为其子树的遍历方式。
因此对应任意一个01树的表达式，总可以表示为'0'+子树表达式+'1'。
因此我们只要考虑如何将子树表达式最小即可。
可以存在多个子树，我们求出每一个子树的表达式，依照字典序排序后即可并入答案，得到树的最小表示。