算法竞赛进阶指南_打卡_题解_0x00
①:最短Hamilton路径:状压dp
https://www.acwing.com/problem/content/93/
给定一张 n 个点的带权无向图,点从 0∼n−1 标号,求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n 行每行 n 个整数,其中第 i 行第 j 个整数表示点 i 到 j 的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
\(1≤n≤20\)
\(0≤a[i,j]≤10^{7}\)
刚开始想了一下最小生成树,后来发现每个点每条边只能走一遍且没有回头路,最小生成树就可以×掉了。
我们观察到数据范围n不大,可以暴力()
我们于是就可以设立\(0\)~\(2^{20}\)的数,以其二进制表达式代表该点有无被探测过。
很容易,我们可以得到一个数组\(f[i][j]\)。\(i\)为目前于点\(i\)停止,\(j\)为目前为止被探测的状态。
我们可以得到状态转移方程\(f[i][j]=min(f[i][j],f[k][p]+mp[k][i])\)。状态\(i\)由状态\(p\)转移过来,而\(mp[i][j]\)代表从\(i\)点到\(j\)点的花费。
输出\(min(f[0...20][2^{20}-1])\)即可。
②:起床困难综合症:模拟,贪心,位运算
https://www.acwing.com/problem/content/1000/
drd 的防御战线由 n 扇防御门组成。
每扇防御门包括一个运算 op 和一个参数 t,其中运算一定是 OR,XOR,AND 中的一种,参数则一定为非负整数。
如果还未通过防御门时攻击力为 x,则其通过这扇防御门后攻击力将变为 x op t。
最终 drd 受到的伤害为对方初始攻击力 x 依次经过所有 n 扇防御门后转变得到的攻击力。
由于 atm 水平有限,他的初始攻击力只能为 0 到 m 之间的一个整数(即他的初始攻击力只能在 0,1,…,m 中任选,但在通过防御门之后的攻击力不受 m 的限制)。
为了节省体力,他希望通过选择合适的初始攻击力使得他的攻击能让 drd 受到最大的伤害,请你帮他计算一下,他的一次攻击最多能使 drd 受到多少伤害。
我们假设对于\(x\)二进制位上的每一位,考虑其是否能取\(0\)或\(1\)。若能取,我们留下标记。
如何取判断第\(i\)位能取?
我们只要枚举为\(0\)和\(1\)的情况,将其进行上述的第\(i\)位\(n\)次运算,观察答案是否使我们的总贪心值小于等于\(m\),如果小于,则合法,否则不取。
核心代码
for(int i=maxx;i>=1;--i){
int Tbit;
int temp=pow(2,i-1);
for(int k=1;k<=2;++k){
Tbit=Ubit[k];
for(int j=1;j<=n;++j){
if(bit[j][0]==-1){
Tbit&=bit[j][i];
}
if(bit[j][0]==-2){
Tbit|=bit[j][i];
}
if(bit[j][0]==-3){
Tbit^=bit[j][i];
}
}
if(Tbit==1){
N+=temp;
ori+=temp*Ubit[k];
if(ori>m){
ori-=temp*Ubit[k];
N-=temp;
}
break;
}
}
}
③:动态中位数:堆,对顶堆
https://www.acwing.com/problem/content/108/
依次读入一个整数序列,每当已经读入的整数个数为奇数时,输出已读入的整数构成的序列的中位数。
输入格式
第一行输入一个整数 P,代表后面数据集的个数,接下来若干行输入各个数据集。
每个数据集的第一行首先输入一个代表数据集的编号的整数。
然后输入一个整数 M,代表数据集中包含数据的个数,M 一定为奇数,数据之间用空格隔开。
数据集的剩余行由数据集的数据构成,每行包含 10 个数据,最后一行数据量可能少于 10 个,数据之间用空格隔开。
假设我们有一个数据结构,存储前\((n+1)/2\)小个数,另一个存储后\((n-1)/2\)小数。
我们每次询问前\((n+1)/2\)个数的最大值,便可得到中位数。
于是我们建立一个对顶堆。
对顶堆就是将一个大堆\(S\)分为两个小堆\(A,B\),堆\(A,B\)没有交集,并且集合\(A+B\)为全集。并且A,B存在逻辑上的连续。(例如\(A\)的堆顶为\(B\)的堆顶)
对于该题,我们将\(n\)个数组成的堆分解为\(A\),\(B\)两个小堆,A为小根堆,B为大根堆。B存储\((n+1)/2\)小个数,A存储后\((n-1)/2\)小数。
对于每个中位数的询问,我们直接返回堆\(B\)的堆顶即可。
建立对顶堆:
------------如何传入值:
①只要堆\(B\)为空,将值\(a\)传入\(B\)必然最优。
②当\(a<B.top()\)时,将值传入\(B\)必然最优。
③否则将值\(a\)传入A中。
------------如何修改\(A\),\(B\)堆信息,使其维护中位数
①当\(A.size()>B.size()\)时,弹出\(A\)的顶端于\(B\)中。
②当\(B.size()>A.size()+1\)时,弹出\(B\)的顶端于\(A\)中。(因为维护中位数,因此\(B,size()\)必然恰好比\(A.size()\)多一)
\(******\)扩展:对顶堆因为其性质,可以动态维护第\(K\)大数。(即使K值在变化
④费解的开关:位运算,递推
https://www.acwing.com/problem/content/description/97/
25 盏灯排成一个 5×5 的方形。
每一个灯都有一个开关,游戏者可以改变它的状态。
每一步,游戏者可以改变某一个灯的状态。
游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字 1 表示一盏开着的灯,用数字 0 表示关着的灯。
给定一些游戏的初始状态,编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。
一共输出 n 行数据,每行有一个小于等于 6 的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态,若 6 步以内无法使所有灯变亮,则输出 −1。
所实话这道题我看了题解也没有搞懂,,,(我暴力暴T)
它有三个性质:
①每一个位置顶多只会操作一次。因为如果操作两次的话,相当于不操作,必然是不满足最优解。
②在一套方案中,操作的顺序无关紧要,这一个略加思索便可得知
③最重要的性质,如果我们确定了第\(i\)行的操作方案的话,那么后面的行数都可以依此递推。
(我不懂性质三咋看出来的)
按我的理解,在我们已经充分理解性质③的条件下,我们枚举所有对第一行的所有操作方案,一共有32种。
我们令有一个循环for(int i=0;i<32;++i)遍历所有第一行操作方案。(\(i\)的第\(j\)位为\(1\)时按下第\((i,j)\)个按钮)
对于每一个第一行的枚举,我们继续在其内枚举\(2...5\)行的可能性
此处不求操作的可能性,而是当我们遇到关灯状态\(0\)时再操作。
假设我们处于第二行,因为对于每一个操作,均会影响其四个方位包括自己的状态。
而在我们第一行枚举完毕的情况下,要求我们不改变第一行的性质,我们只能改变第三行从而改变第二行。
我们将第一,第二,第三行推广向第\(i-1\)行,第\(i\)行,第\(i+1\)行。
即可依次递推直至最后一行,若所有按钮均处于开灯状态,则记录操作次数。
经过所有的枚举,所得最少操作次数即为答案。
uu开开这道题八,浇浇我(((
⑤:分形之城:分治,坐标变换,模拟
https://www.acwing.com/problem/content/100/
算是把以前开过但没有做出来的题AC了,感觉还是挺舒畅的。
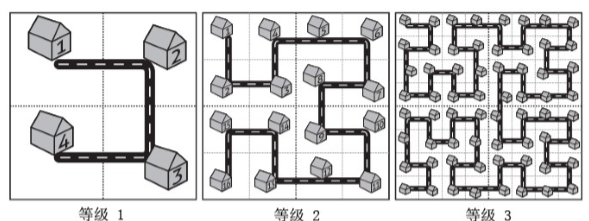
而这座名为 Fractal 的城市设想了这样的一个规划方案,如下图所示:
当城区规模扩大之后,Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围,提升城市的等级。
对于任意等级的城市,我们把正方形街区从左上角开始按照道路标号。
虽然这个方案很烂,Fractal 规划部门的人员还是想知道,如果城市发展到了等级 N,编号为 A 和 B 的两个街区的直线距离是多少。
街区的距离指的是街区的中心点之间的距离,每个街区都是边长为 10 米的正方形。
\(1≤N≤31,\)
\(1≤A,B≤2^{2N},\)
\(1≤n≤1000\)
问题就是让我们求解在题目输入给出的两个城市编号,求欧几里得距离。
数据范围很大,暴力必然不可取。
经过观察,我们可以明显的发现,每一个等级为\(rank\)的城市都是有四个等级为\(rank-1\)的城市组成。
我们记等级为\(rank\)的城市由\(rank-1_{1}\),\(rank-1_{2}\),\(rank-1_{3}\),\(rank-1_{4}\)组成。
并且呈:
\(rank-1_{1}\) \(rank-1_{2}\)
\(rank-1_{4}\) \(rank-1_{3}\)
的组成。
我们记一般的\(rank-1\)呈上述的情况被\(rank-2\)组成。
因此\(rank-1_{1}==rank-1_{向右旋转90°,并且左右翻转}\)
\(rank-1_{2}==rank-1\)
\(rank-1_{3}==rank-1\)
\(rank-1_{4}==rank-1_{向右旋转270°,并且左右翻转}\)
我们就可以对该题使用分治进行模拟()
\(******\)注意:模拟过程中旋转角度过程中以及翻转的次数,均会影响一般\(rank-1\)的状态,因此实现细节比较多。
\(******\)这题比较难,我贴一个我的完整代码,当然别人的题解比我的屎山代码好到不知那里去了((
\(******\)https://www.acwing.com/activity/content/code/content/1835214/
⑥:畜栏预定:贪心,板子题
https://www.acwing.com/problem/content/113/
有 N 头牛在畜栏中吃草。
每个畜栏在同一时间段只能提供给一头牛吃草,所以可能会需要多个畜栏。
给定 N 头牛和每头牛开始吃草的时间 A 以及结束吃草的时间 B,每头牛在 [A,B] 这一时间段内都会一直吃草。
当两头牛的吃草区间存在交集时(包括端点),这两头牛不能被安排在同一个畜栏吃草。
求需要的最小畜栏数目和每头牛对应的畜栏方案。
阅读题目,我们所要求的结果为
给出一堆线段中,可以合并两个没有交集(并且不含端点)的多个线段。
求出最少可以留下几个线段,并且列出第\(i\)个线段对应的合并后线段编号。
根据简单的推理,我们一定可以知道:
①:当有在合并后线段与初始线段排序好的情况下,当有\(e[i].l>e[j].r\)便一定可以将\(i\)并入集合\(j\)中。
并且该操作最优(\(j\)为合并后线段编号)
现在我们考虑如何对这两个线段进行操作。
①我们首先对初始线段的左端点进行升序排序。
②遍历排序后的线段,我们将新加入的线段扔入堆中(可能被合并入旧线段,也可能另起一个线段)。
并且堆以右端点为关键字生成一个小根堆。
为什么我们生成一个小根堆呢?
在我们以左端点排序好的初始线段遍历遍历选取。
我们必然能使\(e[i].l>heap.top()\)时加入合并旧线段,并且为最优答案。
否则我们另起一个新线段。
\(heap.size()\)即为最少留下线段总数,我们只要随便维护一下其id即可求出第\(i\)个线段对应的合并后线段编号。
⑦:袭击:分治,对点最近距离,板子题
https://www.acwing.com/problem/content/121/
这道题目对我的意义非凡啊,算是对我算法竞赛的启蒙啊。所以我觉得大家都应该做
该系统由 N 个核电站供应能源,其中任何一个被摧毁都会使防御系统失效。
将军派出了 N 个特工进入据点之中,打算对能源站展开一次突袭。
不幸的是,由于受到了帝国空军的袭击,他们未能降落在预期位置。
作为一名经验丰富的将军,亚瑟很快意识到他需要重新安排突袭计划。
他现在最想知道的事情就是哪个特工距离其中任意一个发电站的距离最短。
你能帮他算出来这最短的距离是多少吗?
我觉得我以前写的博客就挺好的。bushi
所以因为偷懒就直接放下面了((
https://www.cnblogs.com/Inabameguru/articles/14752944.html
⑧:雷达设备:贪心
https://www.acwing.com/problem/content/114/
雷达装置均位于海岸线上,且雷达的监测范围为 d,当小岛与某雷达的距离不超过 d 时,该小岛可以被雷达覆盖。
我们使用笛卡尔坐标系,定义海岸线为 x 轴,海的一侧在 x 轴上方,陆地一侧在 x 轴下方。
现在给出每个小岛的具体坐标以及雷达的检测范围,请你求出能够使所有小岛都被雷达覆盖所需的最小雷达数目
这题我们有一个小技巧处理一下题目给我们的信息,就可以顺利地转化成贪心解了。
我们对于每一个\(海岛_{i}\),对其求与\(x\)轴上的合法雷达放置映射。
于是乎,我们的求解就变为
对于任意区间\(i\),若存在区间\(j\)与\(i\)存在交集,则在其交集部分放置雷达可以将两个区间合并为一个区间。
求最少剩余区间数。
这就很像上面的 畜栏预定 了对吧。
我们我们可以类似的进行一下贪心。
我们首先按照第一关键字进行排序,左右端点均可,此处我选择以左区间升序排序。如果依照其他方式排序记得等价变换。
在我们以左区间升序排序后,我们以此遍历各个区间。
很明显,其存在一个这样的性质
我们维护一个\(pos\),\(pos\)为最后一个雷达于\(x\)轴上的位置。
在当\(区间_{i}.l>pos\)时,很明显,\(pos\)不能再维护\(区间_{i}\),因此我们另开一个新雷达,最大限度更新\(pos\)的信息。
否则,\(区间_{i}.l\)仍能够被自动维护,不需要新开雷达,因此我们只要最大限度更新\(pos\)信息即可。
我们知道,当\(pos\)取右区间时为最优状态。不过对于不新开雷达的状态下,\(pos\)的上限为\(min(pos,区间_{i}.r)\)。
⑨:防线:二分
https://www.acwing.com/problem/content/description/122/
防线由很多防具组成,这些防具分成了 N 组。
我们可以认为防线是一维的,那么每一组防具都分布在防线的某一段上,并且同一组防具是等距离排列的。
也就是说,我们可以用三个整数 S, E 和 D 来描述一组防具,即这一组防具布置在防线的 S,S+D,S+2D,…,S+KD(K∈Z,S+KD≤E,S+(K+1)D>E)位置上。
如果防线的某个位置有偶数个防具,那么这个位置就是毫无破绽的(包括这个位置一个防具也没有的情况,因为 0 也是偶数)。
只有有奇数个防具的位置有破绽,但是整条防线上也最多只有一个位置有奇数个防具。
作为行动队的队长,lqr 要找到防线的破绽以策划下一步的行动。
题意就很明显的告诉我们要求存在奇数个装备的位置。
因为最多存在一个为奇数的点位。因此存在一个单调性
如果到以\(mid\)为止的区间一共有偶数件,则答案至少存在\(mid\)之后。
否则答案至少存在于\(mid\)本身的位置或\(mid\)之前。
对于\(S,E,D\)的关系,我们可以简单的化解为一个公式即可求出\(mid\)之前的第\(i\)种总数。
关系如下:
\(sum += (min(mid, E_{i})-S_{i}) / D_{i} + 1\)
若存在防线上的缺陷,再在求出缺陷的位置后维护一下以答案为区间末端的装备数量即可。
⑩:糖果传递:数学,推公式,贪心
https://www.acwing.com/solution/content/955/
有 n 个小朋友坐成一圈,每人有 a[i] 个糖果。
每人只能给左右两人传递糖果。
每人每次传递一个糖果代价为 1。
求使所有人获得均等糖果的最小代价。
不会呃呃。
感觉像是均分纸牌,不过这个每次只能移动一个。
感觉向货仓选址,不过这个已经定好位置了。
虽然这题就是货仓选址和环形均分纸牌结合。
就是推公式。反正我是推不出来,当板子题做了
首先我们一定要求出平均数\(ave\),为了求使最终均等的结果。
我们假设有公式\(res=|X_{1}| + |X_{2}| + |X_{3}| + ……+ |X_{n}|\),\(x_{i}\)代表第\(i\)给与第\(i+1\)位的糖果数。
我们现在考虑求\(|X_{i}|\)之和最小,我们理所当然的会想到中位数的性质。
我们知道\(ave=a[i]-x[i]+x[i-1]\),因此\(x[i]=x[i-1]-(ave-a[i])\)。
则有
\(res=∣X_{n}−(ave−a_{1})∣+∣X_{n}−(2ave−(a_{1}+a_{2}))∣+∣X_{n}−(3ave−(a_{1}+a_{2}+a_{3}))∣+…+∣X_{n}∣\)
此处就是货仓选址了,因此我们只要诸如\(ave−a_{1}\)项的中位数,以其中位数代替公式中\(X_{n}\)的即可。
十题分割线-------------------------------------------------------------------------------------------
①:赶牛入圈:二分,离散化,前缀和
https://www.acwing.com/problem/content/123/
我对这道题的记忆清晰,上学期卡我卡到晚上两点还没做出来,今天才一雪前耻。
也是这道题让我从其它更基础的地方学起。现在回头看这道题,除了一些小技巧之外,还是十分明了的。
约翰的土地里一共包含 N 单位的三叶草,每单位三叶草位于一个 1×1 的土地区域内,区域位置由其左下角坐标表示,并且区域左下角的 X,Y 坐标都为整数,范围在 1 到 10000 以内。
多个单位的三叶草可能会位于同一个 1×1 的区域内,因为这个原因,在接下来的输入中,同一个区域坐标可能出现多次。
只有一个区域完全位于修好的畜栏之中,才认为这个区域内的三叶草在畜栏之中。
请你帮约翰计算一下,能包含至少 C 单位面积三叶草的情况下,畜栏的最小边长是多少。
\(1≤C≤500, C≤N≤500\)
我们一看这个数据范围,开个\(a[10000][10000]\)肯定不理想对吧,我们再仔细看这个\(N\)的取值。
才500,\(O(n^3)\)我们都敢大胆尝试了,不过我们如何把这些{\(x,y\)}组成的二元组从\(1\)~\(10000\)映射到关于\(N\)的范围内。
我们自然考虑会离散化的方法。不过这里不太一样,这里是二维坐标下的离散化。
对于一维坐标下的离散化,我们只留下一次出现过的数字,并以其大小关系的顺序赋予索引值。
不过对于二维坐标,我们如何离散化。
我们将二元组{\(x,y\)}中\(x\)与\(y\)拆开,放入离散化数组\(p\)中。
为什么我们将二元组拆开放入\(p\)中呢?
考虑一下,我们如果将\(x,y\)拆开放入\(p\)中,由{\(p_{i}\),\(p_{j}\)}组成的二元组至少可以表示所有的原二元组。
其组成的二元组数量或许会大于原二元组,但是没有关系,我们离散化仍然是成功的,因为它从\(1...10000\)映射到了\(1...1000\)中(因为\(x,y\)加起来可能会有\(1000\)种不同数字)
离散化完成后,我们便可以用\(mp[1007][1007]\)求离散化后矩阵内三叶草的前缀和(为优化后续\(check\)过程)。
我们发现若要求最小边长的正方形围栏中有\(C\)单位的三叶草,就必然要枚举每一个点,以每一个点为基准,尺取不同长度的边长。求出最优解,
然而我们可以发现怎么一个单调性
我们二分选取边长的长度\(mid\)。
如果其边长符合存在\(C\)单位的三叶草,我们必然使\(mid\)更小,才能得出更优解
否则\(mid\)及比\(mid\)更小的边长一定不符合题目要求
因此我们二分选取边长,二分过程中利用前缀和,我们可以在\(O(n^2)\)的时间内得出是否存在有边长为\(mid\)的矩形符合要求。
\(******\)下面讲下我曾经的乱搞算法(划掉)
我首先二分了边长。
然后,,,
我对每一个点开始旋转!!!!!
我们在旋转的过程中,可以完美的将以\(N\)个二元组为顶点每一个正方形取到!
然后

我觉得这个东西是可以成为正解的,有无大兄弟步我后尘捏~
②:耍杂技的牛:贪心,推公式
https://www.acwing.com/problem/content/127/
这题我好像悟到了一个小技巧,,,
这 N 头奶牛中的每一头都有着自己的重量 Wi 以及自己的强壮程度 Si。
一头牛支撑不住的可能性取决于它头上所有牛的总重量(不包括它自己)减去它的身体强壮程度的值,现在称该数值为风险值,风险值越大,这只牛撑不住的可能性越高。
您的任务是确定奶牛的排序,使得所有奶牛的风险值中的最大值尽可能的小。
一看,我就觉得和以前做过的国王游戏特别像啊,我就像国王游戏套一个板子上去
bool operator<(const node a)const
{return w*s<a.w*a.s;}
结果:
woc,好像有戏。
于是我开始尝试手推公式,写了一些等式,结果得到了一个比较简便的玩意
\(T\)代表忍受值,\(W\)代表重量,\(S\)代表力量。
这个鬼玩意,看着没有头绪啊。
我就尝试将\(T_{i-1}\)忽略,直接采用
bool operator<(const node a)const
{return w+s-a.s<a.w+a.s-s;}

woc,不止是有戏了,好像就是正解了。
突发奇想的我,对着最后一组样例,找规律,弄了一个
bool operator<(const node a)const
{return w+s<a.w+a.s;}

AC!!!润了润了,,,
③:士兵:中位数
https://www.acwing.com/problem/content/125/
这道题和货场选址特别像,应该算是扩展了。
格格兰郡中的位置由一对 (x,y) 整数坐标表示。
士兵可以进行移动,每次移动,一名士兵可以向上,向下,向左或向右移动一个单位(因此,他的 x 或 y 坐标也将加 1 或减 1)。
现在希望通过移动士兵,使得所有士兵彼此相邻的处于同一条水平线内,即所有士兵的 y 坐标相同并且 x 坐标相邻。
请你计算满足要求的情况下,所有士兵的总移动次数最少是多少。
需注意,两个或多个士兵不能占据同一个位置。
我们读完题的第一想法就是分别 对\(x,y\)轴求中位数。
不过在第一个操作完成后(无论是将所有点移动到\(x\)的中位数上或\(y\)的中位数上),我们发现会有点重叠。
我们怎么办呢,这一步的思想更离散化很像。
有一个性质:
排序后士兵间的相对顺序和最后走到最终位置的相对顺序不会改变.
我们就可以放心的对移动后的点以相对位置表示。就是将相同坐标上的点以离散化弄到不同的地方上去,不过与其他值的相对位置不变。最后对相对位置求中位数,最后就得答案了。
④:Web of Lies:拓扑图,思维题
https://codeforces.com/contest/1549/problem/C
因为我实在找不到题了,这里就拿一个CF的题划过去。
There are n nobles, numbered from 1 to n. Noble i has a power of i. There are also m "friendships". A friendship between nobles a and b is always mutual.
A noble is defined to be vulnerable if both of the following conditions are satisfied:
the noble has at least one friend, and
all of that noble's friends have a higher power.
You will have to process the following three types of queries.
Add a friendship between nobles u and v.
Remove a friendship between nobles u and v.
Calculate the answer to the following process.
The process: all vulnerable nobles are simultaneously killed, and all their friendships end. Then, it is possible that new nobles become vulnerable. The process repeats itself until no nobles are vulnerable. It can be proven that the process will end in finite time. After the process is complete, you need to calculate the number of remaining nobles.
Note that the results of the process are not carried over between queries, that is, every process starts with all nobles being alive!
Input
The first line contains the integers n and m (1≤n≤2⋅105, 0≤m≤2⋅105) — the number of nobles and number of original friendships respectively.
The next m lines each contain the integers u and v (1≤u,v≤n, u≠v), describing a friendship. No friendship is listed twice.
The next line contains the integer q (1≤q≤2⋅105) — the number of queries.
The next q lines contain the queries themselves, each query has one of the following three formats.
1 u v (1≤u,v≤n, u≠v) — add a friendship between u and v. It is guaranteed that u and v are not friends at this moment.
2 u v (1≤u,v≤n, u≠v) — remove a friendship between u and v. It is guaranteed that u and v are friends at this moment.
3 — print the answer to the process described in the statement.
Output
For each type 3 query print one integer to a new line. It is guaranteed that there will be at least one type 3 query.
Examples
题意就是任何人有联系,如果人存在等级比他高的朋友,就会死去,不会复活。
每当输入询问时,你都要输出现在有多少人活着。可能有多次询问。
我们很明显的可以知道这个题目起码是和图论有关系的。
假设我们在等级低向等级高的朋友连一条有向边,由低级指向高级。如果一个人的出度为\(0\),自然,他也就不会死亡。
理解题意之后,结果我们就是要求有多少个出度为\(0\)的点。
我们只要维护答案即可,不需要一步步模拟,不然会T。