题解 acwing119 袭击 计算几何/对点最近距离

 

 弥宝镇楼,,,

本文包含且不仅限于语言混乱，表述不清，码风凌乱，排版难看等问题,,,

萌新第一次碰计算几何的题目，对点最近距离题目，整了半天才整会QAQ。
一：
前置知识:对点最近距离。
（1）枚举：O（n^2）不讨论。
（2）分治法：O（n*logn*logn），如下：
我们首先考虑一维情况，有：

 

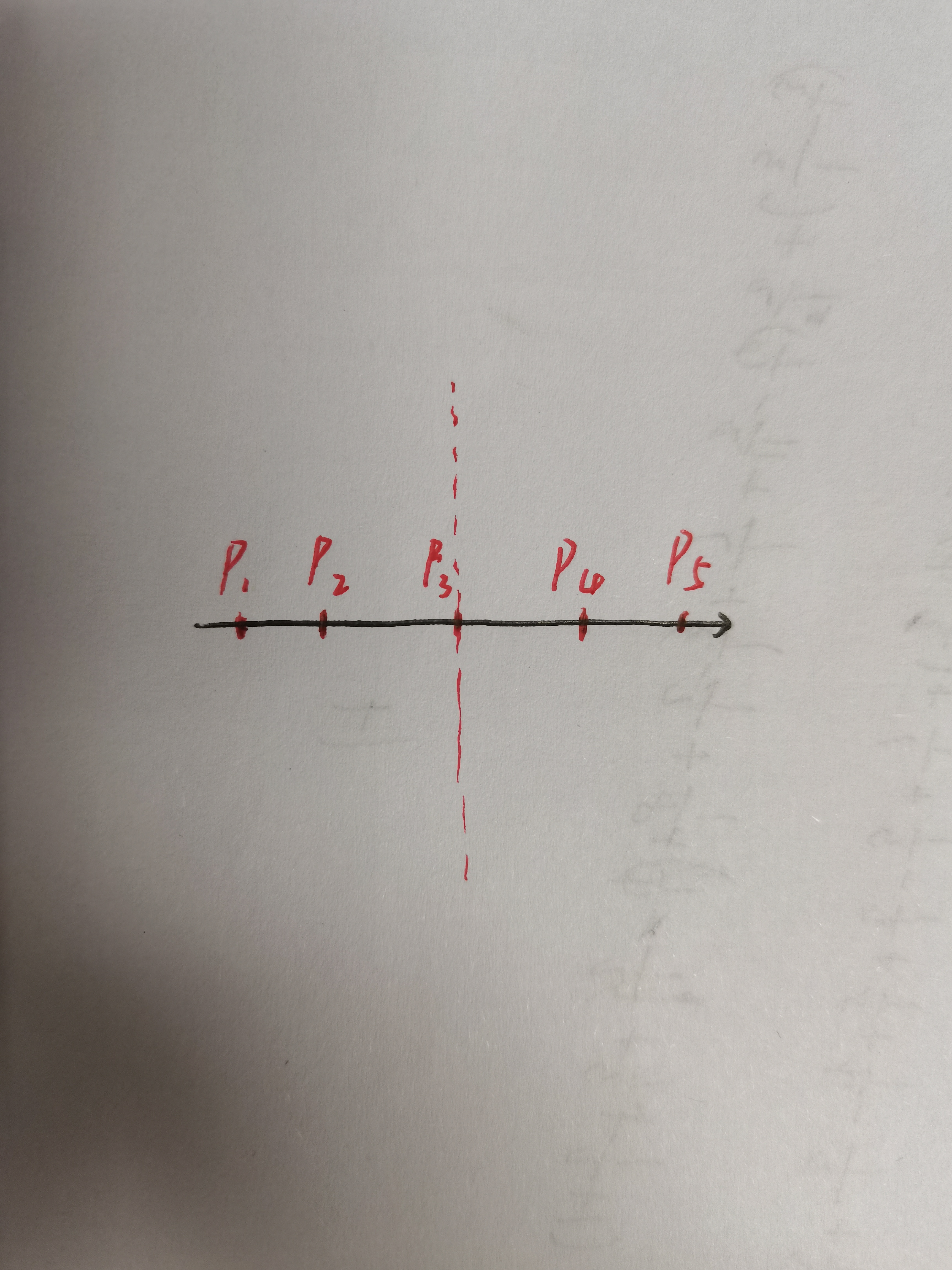
我们先将上述坐标对x坐标由小到大排序。

记全局最小为minn，通过分治的思想，很容易知道minn=min（minn[left,mid],minn[mid+1,right]）;

不过还不够，因为分治还要存在破开[left,mid]与[mid+1,right]的状态，这样我们才能找到全局最小距离。

因此minn在经过以上状态后，还要经历一个minn=min（minn,minn[破开]）的一个公式。

对于minn[left,mid]与minn[mid+1,right]来说，很简单，我们可以直接递归求解，只要设立边界条件left=right与left+1=right就可求出各个状态下的minn值。

如何破开？我们在merge时，找到[left,mid]最右点，[mid+1,right]的最左点就行了。

复杂度O（n*logn*logn）。

其次，我们推广到二维情况，有：

 

 

 

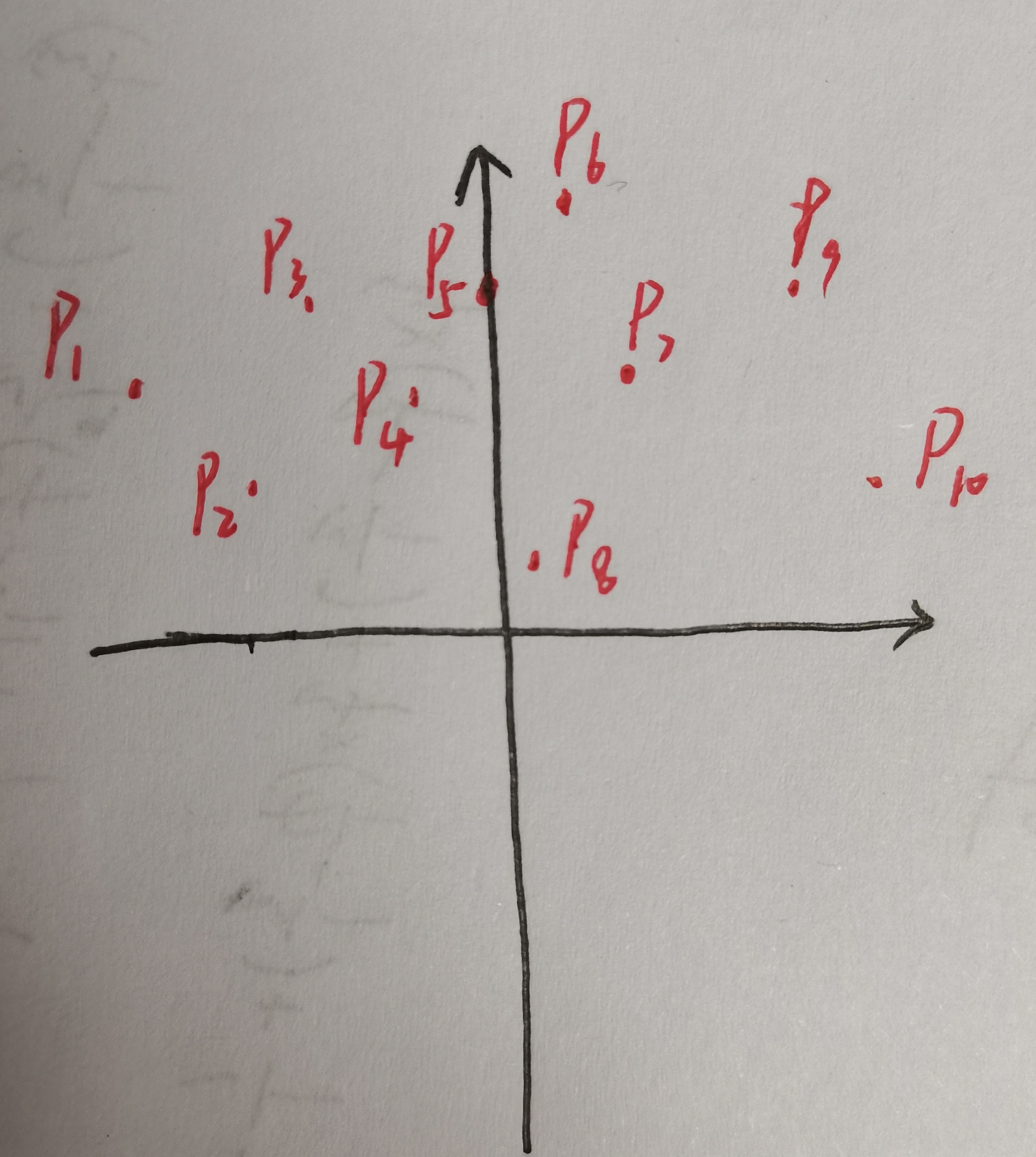
距离会被两个数据改变x轴和y轴。
目前我们先考虑x轴，影响y轴的情况我们有待考察。
相同的，我们将坐标对x升序排序。
我们继续进行分治，同上。
我们建立的边界条件也相同。
（目前我们只对x轴进行考察，y轴还不考虑）
目前为止，我们可以写出一下代码：

struct Point

{

　　int x,y;

} P[maxn],Py[maxn];

double dis（Point A,Point B）
{
　　int tx=A.x-B.x,ty=A.y-B.y;
　　return sqrt（tx*tx-ty*ty）;
}

//每个merge返回一个目前已知最小距离
double merge（int l,int r）
{
　　double minn,dl,dr;
　　int mid=l+r>>1;
　　if（l==r）return inf;
　　if（l+1==r）return dis（P[l]，P[r]）;
　　dl=merge（l,mid）,dr=merge（mid+1,r）;
　　minn=min（dl,dr）;
　　,,,,,,　　//合并操作，对y的考察，从而推出目前已知最小距离（包括破开[left,mid],[mid+1,right]之后）。
　　return minn;
}

 

现在我们要对y进行考察，我们不妨先和x相同，应满足一下条件：
(1)有一个能够存储进行操作的数据结构；
(2)对其数据结构进行排序使其有序；
(3)对其数据结构进行考察，更新minn的值。
其一：我们要引入一个数组，存储数据结构:

int k=0;
for（int i=l;i＜=r;++i）
{

　　//因为破开操作与mid相关，因此我们选择P[mid].x为固定值

　　//只有这样才可能确保Py中有可能出现可能小于minn的值

　　if（abs（P[mid].x-P[i].x）<minn）　

　　Py[++k]=P[i];
}

 

其二：对y升序排序:

sort（）

其三：考察minn值:
考察minn值就要考察y值，因为x值在其一考虑过了，现在我们只要考察dis（Py[?]，Py[??]）即可。（精髓所在啊（以下是线性的

for（int i=1；i<=k;++i）
{

　　//因为我们已经将Py对y升序排序完毕了，并且若有两点距离<minn，
　　
　　其必有Py[j].y-Py[i].y<minn,所以Py[j].y-Py[i].y>=minn时可以直接跳出循环了

　　for（int j=i+1;j<=k&&Py[j].y-Py[i].y<minn;++j）　　

　　{

　　　　double dy=dis(Py[j],Py[i]);

　　　　if(dy<minn)minn=dy;

　　}
}

 

说实话那个东西为什么是线性的我没有太搞懂，怎么看都是n^2啊，反而还退化了？我们就画图一下吧(因为不会计算和证明（

分治过程中，会产生最小矩形使其进行合并过程。

 

可以知道最多存在八个点存在与最小矩形当中（因为大于八个点就不为最小矩形）

因此k的最大值为8。（不过我这个不严谨，实际上不可能到8，只是通俗一点，事实上应该是6（严谨几何证明请见https://www.acwing.com/solution/content/15774/

因为k很小，可以接受，所以这个东西是线性复杂度？

证毕？

 

于是乎，代码就开开心心地打出来了。

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn = 1e5 + 10;
const double inf = 1e30;
int T;
struct Point
{
    double x, y;
} P[2*maxn], Py[2*maxn];
int cmpx(Point A, Point B)
{
    if (A.x != B.x)
        return A.x < B.x;
    return A.y < B.y;
}
int cmpy(Point A, Point B)
{
    return A.y < B.y;
}
inline double min(double A, double B)
{return A > B ? B : A;}
double dis(Point A, Point B)
{
    double tx = A.x - B.x,ty = A.y - B.y;
    return sqrt(tx * tx + ty * ty);
}
double merge(int l, int r)
{
  double minn,dl,dr;
  int mid = l + r >> 1;
  if(l == r)return inf;
  if(l + 1 == r)return dis(P[l],P[r]);
  dl = merge(l,mid),dr = merge(mid + 1,r);
  minn = min(dl,dr);
  int k = 0;
  for(int i = l;i <= r;++i)
  {
      if(abs(P[mid].x - P[i].x)< minn)
      Py[++k] = P[i];
  }
  sort(Py + 1, Py + k + 1, cmpy);
  for(int i = 1;i <= k;++i)
  {
      for(int j = i + 1;j <= k && Py[j].y - Py[i].y < minn;++j)
      {
        double dy = dis(Py[j],Py[i]);
        if (dy < minn)minn = dy;
      }
  }
  return minn;
}
int main()
{
    //freopen("C:\\Users\\Towetrlone\\Desktop\\P1429_1.txt", "r", stdin);
    scanf("%d", &T);
    for (int i = 1;i <= T;++i)
    {
        scanf("%lf%lf", &P[i].x, &P[i].y);
    }
    sort(P + 1, P + T + 1, cmpx);
    printf("%.4lf",merge(1, T));
    return 0;
}

 

不过，本篇还未结束，因为这是袭击题解，而不是对点最近模板（

以上，引入已经结束。

 

二：acwing119. 袭击

题干：

与联盟的战斗中屡战屡败后，帝国撤退到了最后一个据点。

依靠其强大的防御系统，帝国击退了联盟的六波猛烈进攻。

经过几天的苦思冥想，联盟将军亚瑟终于注意到帝国防御系统唯一的弱点就是能源供应。

该系统由 NN 个核电站供应能源，其中任何一个被摧毁都会使防御系统失效。

将军派出了 NN 个特工进入据点之中，打算对能源站展开一次突袭。

不幸的是，由于受到了帝国空军的袭击，他们未能降落在预期位置。

作为一名经验丰富的将军，亚瑟很快意识到他需要重新安排突袭计划。

他现在最想知道的事情就是哪个特工距离其中任意一个发电站的距离最短。

你能帮他算出来这最短的距离是多少吗？

输入格式

输入中包含多组测试用例。

第一行输入整数 TT，代表测试用例的数量。

对于每个测试用例，第一行输入整数 NN。

接下来 NN 行，每行输入两个整数 XX 和 YY，代表每个核电站的位置的 X，YX，Y 坐标。

在接下来 NN 行，每行输入两个整数 XX 和 YY，代表每名特工的位置的 X，YX，Y 坐标。

输出格式

每个测试用例，输出一个最短距离值，结果保留三位小数。

每个输出结果占一行。

数据范围

1≤N≤1000001≤N≤100000,
0≤X,Y≤1000000000

 

如何转化为对点最近问题，我们只要将边界条件转化一下就成功力！

模板条件：

if(l == r)return inf;
if(l + 1 == r)return dis(P[l],P[r]);

记分治出现的矩形中出现核电站的总数为cnt1，出现特工的总数为cnt2；

记有cnt=min(cnt1,cnt2)。

若有cnt==0，记为边界条件，return；

若有cnt>1，继续归并；

若有cnt==1，开始返回对点最近；

边界条件替换为

    cnt = min(cnt1, cnt2);
    if (!cnt)return inf;
    if (cnt == 1)
    {
        int flag = 0;
        int cmp; 
        if (cnt1 == 1)flag = 1;
        else flag = 2;
        if (flag == 1)cmp = pp;
        else cmp = ppp;
        minn = merge(cmp, l, r, minn);
        return minn;
    }
    if (cnt > 1)
    {
        dl= divs(l, mid), dr= divs(mid + 1, r);
    }

我们在合并时对其考察对象在模板中为mid（恒定为中间位置），

而在本题中，我们考察的对象为在cnt>1与cnt==1时均有不同对象（可能是我想复杂了？），

因此我们分别对cnt==1与cnt>1时进行考察。

cnt==1时我们对使cnt为1的P[i]的key值为mid值，

而在cnt>1时我们无所谓，我们进行的是合并操作，因此mid仍为中点值。

因此将模板中

  int k = 0;
  for(int i = l;i <= r;++i)
  {
      if(abs(P[mid].x - P[i].x)< minn)
      Py[++k] = P[i];
  }
  sort(Py + 1, Py + k + 1, cmpy);
  for(int i = 1;i <= k;++i)
  {
      for(int j = i + 1;j <= k && Py[j].y - Py[i].y < minn;++j)
      {
        double dy = dis(Py[j],Py[i]);
        if (dy < minn)minn = dy;
      }
  }

 

替换为

double merge(int mid,int l,int r,double minn)
{
    int k = 0;
    double dy = inf;
    for (int i = l;i <= r;++i)
    {
        if (abs(P[mid].x - P[i].x) < minn&&P[mid].flag != P[i].flag)
        {
            Py[++k] = P[i];
        }
    }
    sort(Py + 1, Py + k + 1, cmpy);
    for (int j = 1;j <= k && Py[j].y - P[mid].y < minn;++j)
    {
        if (Py[j].flag == P[mid].flag)continue;
        dy = dis(Py[j], P[mid]);
        minn = min(minn, dy);
    }
    return minn;
}

 

然后我们就可以愉快的AC了！

代码如下：

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const double inf = 1e30 + 5;
const int maxn = 1e5 + 10;
int N;
struct Point
{
    int flag;
    int x, y;
}P[2*maxn],Py[2*maxn];
int cmpx(Point A, Point B)
{
    if (A.x != B.x)
        return A.x < B.x;
    return A.y < B.y;
}
int cmpy(Point A, Point B)
{
    return A.y < B.y;
}
inline double min(double A, double B)
{return A > B ? B : A;}
double dis(Point A, Point B)
{
    double tx = A.x - B.x,ty = A.y - B.y;
    return sqrt(tx * tx + ty * ty);
}
double merge(int mid,int l,int r,double minn)
{
    int k = 0;
    double dy = inf;
    for (int i = l;i <= r;++i)
    {
        if (abs(P[mid].x - P[i].x) < minn&&P[mid].flag != P[i].flag)
        {
            Py[++k] = P[i];
        }
    }
    sort(Py + 1, Py + k + 1, cmpy);
    for (int j = 1;j <= k && Py[j].y - P[mid].y < minn;++j)
    {
        if (Py[j].flag == P[mid].flag)continue;
        dy = dis(Py[j], P[mid]);
        minn = min(minn, dy);
    }
    return minn;
}
double divs(int l, int r)
{
    int pp, ppp;
    int cnt1=0, cnt2=0, cnt=0;
    double minn=inf, dl=inf, dr=inf, dy=inf;
    int mid = l + r >> 1;
    for (int i = l;i <= r;++i)
    {
        if (P[i].flag)
        {
            ppp = i;
            ++cnt2;
        }
        else
        {
            pp = i;
            ++cnt1;
        }
    }
    cnt = min(cnt1, cnt2);
    if (!cnt)return inf;
    if (cnt == 1)
    {
        int flag = 0;
        int cmp; 
        if (cnt1 == 1)flag = 1;
        else flag = 2;
        if (flag == 1)cmp = pp;
        else cmp = ppp;
        minn = merge(cmp, l, r, minn);
        return minn;
    }
    if (cnt > 1)
    {
        dl= divs(l, mid), dr= divs(mid + 1, r);
    }
    minn = min(dl, dr);
    minn = merge(mid, l, r, minn);
    return minn;
}
int main()
{
    int T;
    scanf("%d", &T);
    while (T--) 
    {
        scanf("%d", &N);
        for (int j = 0;j <= 1;++j)
        {
            for (int i = 1;i <= N;++i)
            {
                P[i+j*N].flag = j;
                scanf("%d%d", &P[i+j*N].x, &P[i+j*N].y);
            }
        }
        sort(P + 1, P + 2*N + 1, cmpx);
        printf("%.3lf\n", divs(1, 2*N));
    }
    return 0;
}

祝各位ACMer，OIerAK全场！！