NOIP2005 过河
描述
在河上有一座独木桥，一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子，青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数，我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点：0，1，……，L（其中L是桥的长度）。坐标为0的点表示桥的起点，坐标为L的点表示桥的终点。青蛙从桥的起点开始，不停的向终点方向跳跃。一次跳跃的距离是S到T之间的任意正整数（包括S,T）。当青蛙跳到或跳过坐标为L的点时，就算青蛙已经跳出了独木桥。
题目给出独木桥的长度L，青蛙跳跃的距离范围S,T，桥上石子的位置。你的任务是确定青蛙要想过河，最少需要踩到的石子数。
对于30%的数据，L <= 10000；
对于全部的数据，L <= 10^9。
格式
输入格式
输入的第一行有一个正整数L（1 <= L <= 10^9），表示独木桥的长度。第二行有三个正整数S，T，M，分别表示青蛙一次跳跃的最小距离，最大距离，及桥上石子的个数，其中1 <= S <= T <= 10，1 <= M <= 100。第三行有M个不同的正整数分别表示这M个石子在数轴上的位置（数据保证桥的起点和终点处没有石子）。所有相邻的整数之间用一个空格隔开。
输出格式
输出只包括一个整数，表示青蛙过河最少需要踩到的石子数。
样例1
样例输入1
10
2 3 5
2 3 5 6 7
样例输出1
2
限制
1s
经典状态压缩DP
F[i]=min{F[j]}+1 j∈[i-S,i-T]
从数据范围109来看，直接DP不是TLE就是MLE，所以不能硬怼
桥长109，石子只有100个，最远跳10格，就算石子在怎么平均分配，两个石子之间都有107的长度是空着的，这段距离任凭青蛙怎么跳，最少踩到的石子数都不会变。
那么问题来了，石子之间距离多少时可以进行压缩？
我们先画个数轴
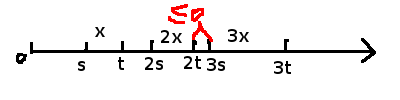
为了更好说明：这里的0不是指原点，表示青蛙当前位置
假设0前面就是一块石子，从0开始后的点都是空地，S~T之间的n*x表示青蛙能到达的位置，当红色区域间隔≤0时，后面将不再有青蛙到不了的地方，因此后面的区域能够到任意位置
证明开始：
设T-S=Δx
nS-(n-1)T<=0
nS-nT+T<=0
T<=n(T-S)
T<=n*Δx
因此：
n=ceil(T/Δx)
间隔的距离为n*T
Δx=1时，n=T最大
因此间隔距离最大为T2，T=10最大，因此最大间隔距离为T2=100
为什么不是n*S呢？青蛙跳过0前的石子后，不一定就到0上，也可能到了0~T-1的位置上，0～T-1包括0～S这一段，这些点也要包括，因此是n*T。
不过要注意：Δx=0 时，也就是S=T时需要特判
这个时候，直接判断石子位置，M[i]%S==0，即可
1 #include<iostream>
2 #include<cstdio>
3 #include<cstring>
4 #include<cmath>
5 #include<algorithm>
6 using namespace std;
7
8 const int MAXN=1E6;
9 const int MAXM=105;
10 const int MOD=100;
11
12 int l,s,t,m,ans=0x7fffffff;
13 int M[MAXM],F[MAXN];
14 bool stone[MAXN];
15
16 int main()
17 {
18 memset(F,0x7f,sizeof(F));
19 F[0]=0;
20 scanf("%d",&l);
21 scanf("%d %d %d",&s,&t,&m);
22 for(int i=1;i<=m;i++)
23 scanf("%d",&M[i]);
24 sort(M+1,M+m+1);
25 if(s==t)
26 {
27 ans=0;
28 for(int i=1;i<=m;i++)
29 if(M[i]%s==0)
30 ans++;
31 cout<<ans<<endl;
32 return 0;
33 }
34 for(int i=1;i<=m;i++)
35 {
36 int x=M[i]-M[i-1];
37 M[i]=M[i-1]+x%MOD;
38 stone[M[i]]=1;
39 }
40 for(int i=1;i<=M[m]+t;i++)
41 {
42 for(int j=s;j<=t;j++)
43 if(i-j>=0)
44 F[i]=min(F[i],F[i-j]);
45 if(stone[i]) F[i]++;
46 }
47 for(int i=M[m];i<=M[m]+t;i++)
48 ans=min(ans,F[i]);
49 cout<<ans<<endl;
50 return 0;
51 }
52
