[无聊/科普向] 一篇关于《原神》抽卡概率/期望计算的正经介绍

注:本文的正确性建立在目前广为流传的一份角色池与武器池单抽出货概率数据之上,详见文章 2.1 与 2.3 部分。
0 省流版
角色池:
- 从零开始抽出一个五星角色期望抽数:\(62.3\),中位抽数:\(75\),最大概率抽数:\(77\)
- 从零开始抽出一个目标 UP 五星角色期望抽数:\(93.4\),中位抽数:\(80\),最大概率抽数:\(77\)
- 从零开始抽出满命目标 UP 五星角色期望抽数:\(654.1\),中位抽数:\(653\),最大概率抽数:\(644\)
武器池:
- 从零开始抽出一把五星武器期望抽数:\(53.3\),中位抽数:\(64\),最大概率抽数:\(66\)
- 从零开始抽出一把目标 UP 五星武器期望抽数:\(105.7\),中位抽数:\(98\),最大概率抽数:\(66\)
- 从零开始抽出满精目标 UP 五星武器期望抽数:\(528.3\),中位抽数:\(526\),最大概率抽数:\(531\)
能衡量“欧非”程度的最直接指标是在前多少抽内出货的累计概率。上述六种情况的累积概率图象见文章 2.2 与 2.3 对应部分。
1 文章介绍
每一位热衷于或受苦于在《原神》中抽卡的玩家都希望有一个直观的指标来帮助自己判断自己的“欧非”程度。此时,出货关于抽数的概率分布以及出货的期望次数成为了玩家们想要获取到的信息。然而,大部分对概率与期望计算方法较为陌生的玩家面对游戏抽卡说明中的一堆数据表现得茫然。打开一些相关视频的评论区,你甚至能找到“抽卡保底数是 \(90\),所以期望出货次数就是 \(90\)”这样的评论。
本文的目的便是教会你正确计算出“省流版”部分中给出的所有数据,并对《原神》抽卡模型的设计进行一定的分析。
2 主要流程
2.1 基础数据获取
我们首先以角色 UP 池为例。
要想进行具体的计算,我们首先需要获取到单抽得到五星角色(即“出货”)的概率。你可能会认为,在祈愿说明中给出的“5 星角色祈愿的基础概率为 \(0.600\%\)”正是我们所需要的数据,实则不然。否则,如果每抽出货的概率恒定,不会产生 \(90\) 抽保底的机制。
我们从一些地方可以获取到这样一个函数:在累计 \(i - 1\) 次抽卡未出货后,第 \(i\) 次出货的概率 \(p(i)\) 满足
也即,前 \(73\) 次抽卡出货的概率均为 \(0.6\%\),从第 \(74\) 抽开始,概率每抽增长 \(6\%\),直到 \(100\%\)。
这是目前网络上流传最广泛的单抽概率数据。这一函数的深层来源我们不得而知,但它的确满足这样一些基本条件:以 \(0.6\%\) 作为基础概率;保底为 \(90\) 抽;主观上满足抽卡的实际情形;表示形式较为简单(这样的概率的设计可能需要经过较多推敲,但最终形式往往不会复杂)。我们姑且信之,并将其用于接下来的具体计算。
2.2 具体计算
2.2.1 抽五星(忽略 UP 与否)角色
我们首先计算从零开始抽卡出货(仅考虑五星,忽略 UP 与否)关于抽数的概率分布。
设 \(P(i)\) 表示从零开始恰好在第 \(i\) 抽出货的概率。也许你可以轻易地写出 \(P(i) = p(i) \cdot \prod\limits_{j = 1}^{i - 1}(1 - p(j))\),但在这里,我们用一个略显复杂的方式表示它:再设 \(f(i)\) 表示前 \(i\) 抽均没有出货的概率,从而列出方程组:
并且有
这样表示的好处我们很快就会看到。依据该方程组的形式,我们可以迭代地从 \(f(0)\) 开始依次计算 \(f(1), P(1), \cdots, f(90), P(90)\)。出货的期望抽数 \(E = \sum\limits_{i = 1}^{90}i \cdot P(i)\)。
我们简单地写一份 Python 代码完成这一计算并输出结果:
import matplotlib.pyplot as plt
import numpy as np
PITY = 90
f = np.zeros(PITY)
result = np.zeros(PITY + 1)
single_rate = [0.006] * (PITY + 1)
for i in range(74, 91):
single_rate[i] = min((1.0, single_rate[i - 1] + 0.06))
### Calculate
f[0] = 1
for i in range(0, PITY):
if i + 1 < PITY:
f[i + 1] = f[i] * (1 - single_rate[i + 1])
result[i + 1] += f[i] * single_rate[i + 1]
presum = np.zeros(PITY + 1)
expect = 0
for i in range(1, PITY + 1):
presum[i] = presum[i - 1] + result[i]
expect += result[i] * i
print("%i: %.10lf %.10lf" % (i, result[i], presum[i]))
print("Expect: %.6lf" % (expect))
print("Debug: %.10lf" % (presum[PITY]))
### Draw function image
fig, ax = plt.subplots(2, 1)
ax[0].plot(np.arange(0, PITY + 1), result * 100)
ax[1].plot(np.arange(0, PITY + 1), presum * 100)
for i in range(0, 2):
ax[i].grid(True)
ax[i].set_ylabel('(%)')
ax[i].set_xlim([0, PITY])
ax[0].set_ylim([0, 11])
ax[1].set_ylim([0, 102])
ax[1].set_xlabel('Pulls')
plt.savefig('result')
plt.show()
输出的期望抽数 \(E_1 = 62.297332\)。\(P(i)\) 本身及其前缀和关于抽数的图象如下(前缀和则表示在前 \(i\) 抽内出货的概率,这便是衡量“欧非”程度的最直接指标):
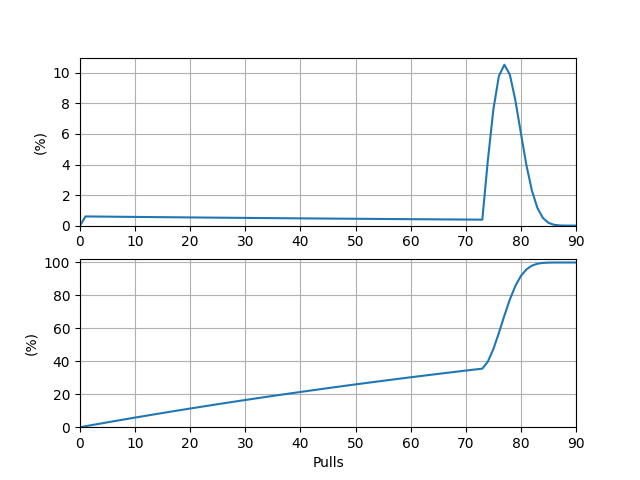
\(P(i)\) 图象的峰值位于点 \((77, 0.105)\) 处,这表明从零开始抽卡,最有可能在第 \(77\) 抽时出货,概率约为 \(10.5\%\)。前缀和图象的 \(50\%\) 对应的抽数在 \(75\) 与 \(76\) 之间,距 \(75\) 更近,这表明中位抽数约为 \(75\)。至此,我们得到了“省流版”中的第一行数据。
2.2.2 抽五星 UP 角色
当我们的目标仅落在 UP 角色上时,一些潜在的变量被引入了进来:是否是大保底,以及若是大保底,又已经累计了多少抽。在 2.2.1 部分中仅用一个变量 \(i\) 控制函数 \(f\) 便不再可取。
仍设 \(P(i)\) 表示从零开始恰好在第 \(i\) 抽出货的概率。设 \(f(i, j, x)(x \in \{0, 1\})\) 表示在前 \(i\) 抽没有抽到目标 UP 角色,且保底情况为 \(x\)(\(0\) 为小保底,\(1\) 为大保底),保底累计抽数为 \(j\) 的概率。注意到当处于小保底时,有 \(0.5\) 的概率获取到想要的 UP 角色,还有 \(0.5\) 的概率“歪”,因此可以列出方程组:
并且有
关于 \(f\) 的方程组中的第三个方程的含义为:如果在小保底阶段抽中了五星角色,且为非 UP(概率为 \(0.5\)),则清空保底的累计抽数,进入大保底阶段。
利用含参量 \(f\) 来计算 \(P\) 的好处此时便得以体现——当需要考虑的情况变得复杂时,我们可以通过增加参数变量来沿用之前的计算方法。\(f\) 仍然可以迭代计算,只需要分别从小到大枚举 \(i, j\)。
沿用上面部分的代码,做一些基础修改后,核心计算部分如下:
MAX_PULLS = 180
PITY = 90
f = np.zeros((MAX_PULLS, PITY, 2))
result = np.zeros(MAX_PULLS + 1)
### Calculate
f[0][0][0] = 1
for i in range(0, MAX_PULLS):
for j in range(0, min((i + 1, PITY))):
if i + 1 < MAX_PULLS and j + 1 < PITY:
for x in range(0, 2):
f[i + 1][j + 1][x] += f[i][j][x] * (1 - single_rate[j + 1])
if i + 1 < MAX_PULLS:
f[i + 1][0][1] += f[i][j][0] * single_rate[j + 1] * 0.5
result[i + 1] += f[i][j][0] * single_rate[j + 1] * 0.5
result[i + 1] += f[i][j][1] * single_rate[j + 1]
输出的期望抽数 \(E_2 = 93.445998\)。事实上,它恰好为 \(E_1 = 62.297332\) 的 \(1.5\) 倍,这是因为若在小保底阶段就出 UP 角色,则期望抽数为 \(E_1\),而若在大保底阶段才出 UP 角色,则期望抽数为 \(2E_1\),因此 \(E_2 = 0.5 \cdot E_1 + 0.5 \cdot 2E_1 = 1.5E_1\)。\(P(i)\) 本身及其前缀和关于抽数的图象如下:
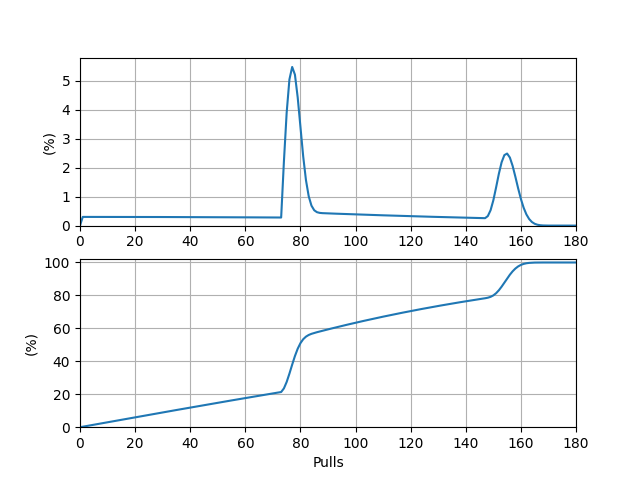
\(P(i)\) 图象的峰值位于点 \((77, 0.0548)\) 处,这表明从零开始抽卡,最有可能在第 \(77\) 抽时出目标 UP 角色,概率约为 \(5.48\%\)。前缀和图象的 \(50\%\) 对应的抽数在 \(79\) 与 \(80\) 之间,距 \(80\) 更近,这表明中位抽数约为 \(80\)。
2.2.3 抽满命五星 UP 角色
对于 \(f\),在 2.2.2 部分的基础上再引入一个参变量 \(k\) 表示已经获取的 UP 角色数,即设 \(f(i, j, k, x)(x \in \{0, 1\})\) 表示在前 \(i\) 抽没有抽满目标 UP 角色,保底情况为 \(x\)(\(0\) 为小保底,\(1\) 为大保底),保底累计抽数为 \(j\),且已经获得了 \(k\) 个 UP 角色的概率。据此可以列出方程组(\(k = 0, 1, \cdots, 6\),其余变量范围略):
并且有
关于 \(f\) 的方程组中的第四个方程的含义为:如果抽中了 UP 五星角色,则清空保底的累计抽数,重新进入小保底阶段,且抽出的 UP 角色数增加 \(1\)。\(f\) 仍然可以迭代计算,只需要分别从小到大枚举 \(i, j, k\)。
仍然沿用上面部分的代码,做一些基础修改后,核心计算部分如下:
MAX_PULLS = 180 * 7
PITY = 90
f = np.zeros((MAX_PULLS, PITY, 7, 2))
result = np.zeros(MAX_PULLS + 1)
### Calculate
f[0][0][0][0] = 1
for i in range(0, MAX_PULLS):
for j in range(0, min((i + 1, PITY))):
result[i + 1] += f[i][j][6][0] * single_rate[j + 1] * 0.5
result[i + 1] += f[i][j][6][1] * single_rate[j + 1]
for k in range(0, 7):
if i + 1 < MAX_PULLS:
if j + 1 < PITY:
for x in range(0, 2):
f[i + 1][j + 1][k][x] += f[i][j][k][x] * (1 - single_rate[j + 1])
f[i + 1][0][k][1] += f[i][j][k][0] * single_rate[j + 1] * 0.5
if k < 6:
f[i + 1][0][k + 1][0] += f[i][j][k][0] * single_rate[j + 1] * 0.5
f[i + 1][0][k + 1][0] += f[i][j][k][1] * single_rate[j + 1]
输出的期望抽数 \(E_3 = 654.121986\)。事实上,它恰好为 \(E_2 = 93.445998\) 的 \(7\) 倍。\(P(i)\) 本身及其前缀和关于抽数的图象如下:
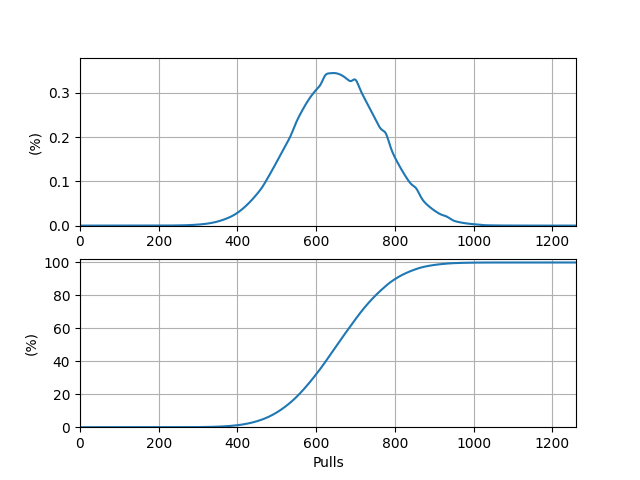
\(P(i)\) 图象的峰值位于点 \((644, 0.00345)\) 处,这表明从零开始抽卡,最有可能在第 \(644\) 抽时出满命的目标 UP 角色,概率约为 \(0.345\%\)。前缀和图象的 \(50\%\) 对应的抽数在 \(653\) 与 \(654\) 之间,距 \(653\) 更近,这表明中位抽数约为 \(653\)。
2.3 进一步结果
抽取武器与抽取角色总体类似,获取到的函数 \(p\) 如下:
此外,在抽取 UP 武器时还需考虑定轨机制,但这仅是在 \(f\) 中添加一个参变量的事。例如,在计算抽满精目标五星 UP 武器的相应概率时,我们将会设 \(f(i, j, k, l, x)\) 表示在前 \(i\) 抽没有抽满目标 UP 武器,保底情况为 \(x\)(\(0\) 为小保底,\(1\) 为大保底),保底累计抽数为 \(j\),定轨数值为 \(k\),且已经获得了 \(l\) 把目标 UP 武器的概率。各个抽取目的下的具体分析略,这里仅给出最终结果。
2.3.1 抽五星(忽略 UP 与否)武器
抽取一把五星武器(忽略 UP 与否)的期望抽数 \(E_4 = 53.250420\)。\(P(i)\) 本身及其前缀和关于抽数的图象如下:
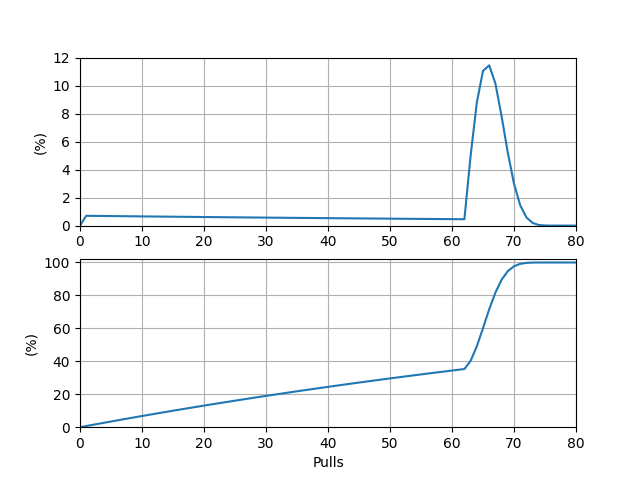
\(P(i)\) 图象的峰值位于点 \((66, 0.114)\) 处。前缀和图象的 \(50\%\) 对应的抽数在 \(64\) 与 \(65\) 之间,距 \(64\) 更近。
2.3.2 抽五星 UP 武器
抽取一把目标五星 UP 武器的期望抽数 \(E_5 = 105.668802\)。\(P(i)\) 本身及其前缀和关于抽数的图象如下:
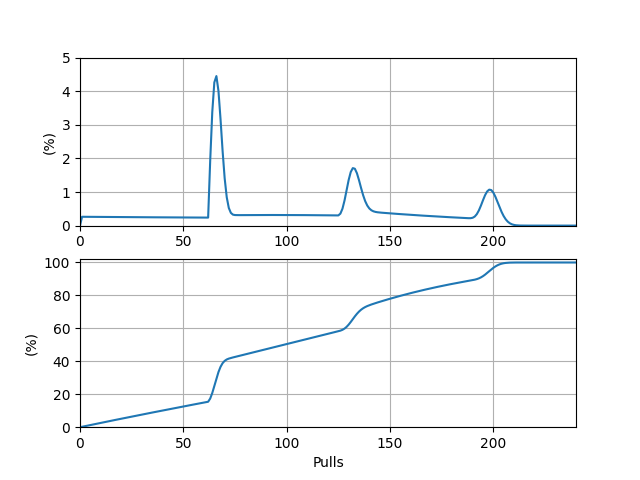
\(P(i)\) 图象的峰值位于点 \((66, 0.0445)\) 处。前缀和图象的 \(50\%\) 对应的抽数在 \(98\) 与 \(99\) 之间,距 \(98\) 更近。
2.3.3 抽满精五星 UP 武器
抽取满精目标五星 UP 武器的期望抽数 \(E_6 = 528.344012\)。\(P(i)\) 本身及其前缀和关于抽数的图象如下:
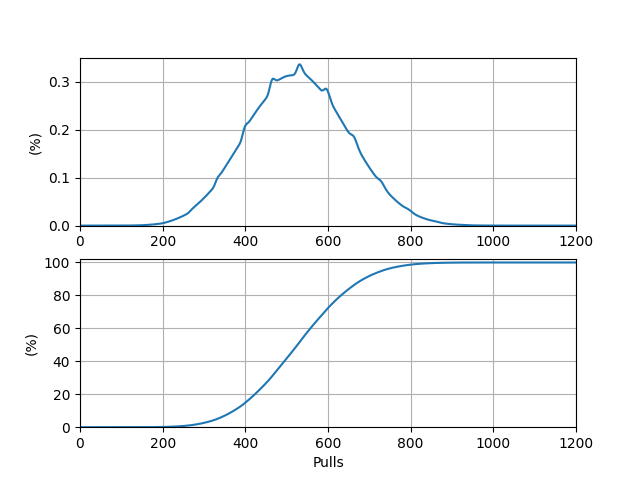
\(P(i)\) 图象的峰值位于点 \((531, 0.00336)\) 处。前缀和图象的 \(50\%\) 对应的抽数在 \(526\) 与 \(527\) 之间,距 \(526\) 更近。
3 模型分析
我们的分析均基于上面计算得到的数据与图象。
3.1 模型优点
当我们观察 2.2.3 与 2.3.3 部分求得的两幅 \(P(i)\) 图象时,也许会惊异于其近似为正态分布,或者它们的前缀和图象足够光滑美观。正态分布通常是我们最能接受的概率分布,尤其是在抽取满命角色或满精武器这样投入周期较长或资源较大的抽卡模型中——当我们付出较多时,我们希望回报等级至少在分布上足够均衡,这样我们既能对获取高等级回报抱以足够的期待,同时又不必太担心自己的收获很差。在面对部分抽卡评价系统给出的“非酋”等级的评估时,许多玩家甚至仅仅希望变得更“平庸”一些,即接近中间水平。正态分布模型给予了他们归宿。
站在游戏策划的角度,单抽出金(这里指角色池)的抽数集中在 \(77\) 抽左右这一设计也较为巧妙。一方面,它离 \(0\) 抽有足够的距离,这保证了绝大多数人在为角色买单时都需要付出足够的代价,更直白地说,它保证了游戏的收入;另一方面,它在从零开始的第八个“十连”末尾,却又没有进入到真正吃满保底需要的第九个“十连”中,这会使大部分玩家庆幸于自己没有“脸黑”,从而产生“提前出货”的主观满足。
3.2 模型缺陷
尽管在上一部分模型优点中,我们对抽取满命角色或满精武器的概率分布给予了一定的肯定,但不要忘记了,原神作为一款免费游戏,其中的大部分玩家并没有抽取满命角色与满精武器的精力与资本。我们还应将视线放回到抽取单个五星角色/武器的概率分布上。可惜的是,我们看到的结果并不尽如人意。
以抽取单个五星角色(忽略 UP 与否)为例。尽管出货的中位抽数和最大概率抽数在 \(76\) 附近,相应图象表明分布也确实较为集中,但期望抽数却仅有 \(62.3\)。这说明在 \(74\) 抽(依据函数 \(p\),出货概率开始提升的时候)之前出货的概率虽然较小,却不可忽略。事实上,前缀和给出在前 \(74\) 抽出货的概率已经超过了 \(1/3\)!这会导致的最直接后果便是大量的幸存者偏差现象——不小的提前出货的概率使一部分人尝到了甜头,这种喜悦蔓延到更大部分保守出货的人面前时,他们就会在默默承受痛苦之余感慨一句“吃柠檬,陌生人!”,并对整个抽卡系统充满抱怨。
武器池设计的不平衡更为明显。从抽取五星角色到抽取五星 UP 角色,最大概率抽数 \(77\) 保持不变,中位抽数仅仅从 \(75\) 提升到了 \(80\),并且它们都在 \(77\) 的附近。但同样是保持一致的最大概率抽数,从抽取五星武器到抽取目标五星 UP 武器,中位抽数从 \(64\) 直接提升为了 \(98\),后者已经远远大于了最大概率抽数 \(66\)。中位数与众数的较大差距表明了模型设计必然存在着不合理之处,同时,这一比较也表明引入定轨机制仅仅防止了如某经典“天空之卷”事件的小概率情形的发生,武器池更深层次的隐患仍没有被清除。
4 其他说明
本文用于数据计算与图象生成的所有代码均可在 https://cloud.tsinghua.edu.cn/d/e5ec914057084c56869c/ 查看。
本文中用到的计算概率函数 \(f\) 的思想实际名为“动态规划”,但由于本文力求科普,所涉及的转移也并不复杂,因此在前面隐匿了这一名称,并且将状态转移方程族简单地称为“方程组”。实际上,每个等式的含义已经由等式本身直接体现,但在必要处我们仍进行了解释说明。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号