经典的同态滤波算法的优化及其应用参数配置。
同态滤波,网络上有很多文章提到过这个算法,我们摘取百度的一段文字简要的说明了该算法的核心: 同态滤波是一种减少低频增加高频,从而减少光照变化并锐化边缘或细节的图像滤波方法。
关于该算法,网络上已经有很多资料了,也有很多给出了参考代码,但是很痛心的是我看到的没有一个是完全正确的,或多或少都存在瑕疵,有些虽然算法最后的效果是差不多正确的,实际上是和真正的算法是背道而驰的。
我们在这里只有简单的语句来描述下该算法的过程。
对于一幅图像f(x,y),可以表示为照射分量i(x,y)和反射分量r(x,y)的乘积。其中0<i(x,y)<∞,0<r(x,y)<1。i(x,y)描述景物的照明,变化缓慢,处于低频成分。r(x,y)描述景物的细节,变化较快,处于高频成分。因为该性质是乘性的,所以不能直接使用傅里叶变换对i(x,y)和r(x,y)进行控制,因此可以先对f(x,y)取对数,分离i(x,y)和r(x,y)。令z(x,y) = ln f(x,y) = ln i(x,y) + ln r(x,y)。由于f(x,y)的取值范围为[0, L-1],为了避免出现ln(0)的情况,故采用ln ( f(x,y) + 1 ) 来计算。
然后取傅里叶变换,得到 Z(u,v) = Fi(u,v) + Fr(u,v)。
然后使用一个滤波器,对Z(u,v)进行滤波,有 S(u,v) = H(u,v) Z(u,v) = H(u,v)Fi(u,v) + H(u,v)Fr(u,v)。
滤波后,进行反傅里叶变换,有 s(x, y) = IDFT( S(u,v) )。
最后,反对数(取指数),得到最后处理后的图像。g(x,y) = exp^(s(x,y)) = i0(x,y)+r0(x,y)。由于我们之前使用ln ( f(x,y)+1),因此此处使用exp^(s(x,y)) - 1。 i0(x,y)和r0(x,y)分别是处理后图像的照射分量和入射分量。
这个滤波器通常我们取如下形式:
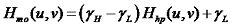
其中,
γL< 1,γH >1,控制滤波器幅度的范围。Hhp通常为高通滤波器,如高斯(Gaussian)高通滤波器、巴特沃兹(Butterworth)高通滤波器、Laplacian滤波器等。
如果Hhp采用Gaussian高通滤波器,则有:
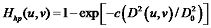
其中,c为一个常数,控制滤波器的形态,即从低频到高频过渡段的陡度(斜率),其值越大,斜坡带越陡峭,见下图。
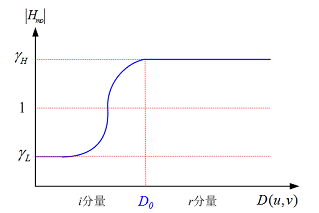
图2 同态滤波器幅频曲线
如果英文可以的,直接看http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/OWENS/LECT5/node4.html这篇文章。
其实过程很简单,但是很多博文都给出了错误的代码,比如在图像增强处理之:同态滤波与Retinex算法(一)同态滤波一文中,其给出的主要代码如下:
function I3 = homofilter(I) %同态滤波函数
subplot(1,2,1),imshow(I);title('同态滤波之前原始图像');
I=double(rgb2gray(I));
[M,N]=size(I);
rL=0.5;
rH=5;%可根据需要效果调整参数
c=3;
d0=9;
I1=log(I+1);%取对数
FI=fft2(I1);%傅里叶变换
n1=floor(M/2);
n2=floor(N/2);
for i=1:M
for j=1:N
D(i,j)=((i-n1).^2+(j-n2).^2);
H(i,j)=(rH-rL).*(exp(c*(-D(i,j)./(d0^2))))+rL;%高斯同态滤波
end
end
I2=ifft2(H.*FI);%傅里叶逆变换
I3=real(exp(I2));
subplot(1,2,2),imshow(I3,[]);title('同态滤波增强后');
我们看看其传递函数H那一行的代码:
H(i,j)=(rH-rL).*(exp(c*(-D(i,j)./(d0^2))))+rL;%高斯同态滤波
很明显,这里有着严重的错误,1-exp操作,他直接写成了exp。虽然他最后得到了一个似乎不错的结果,但是这是违背科学的。
再比如同态滤波及其实现 这篇文章其实也是不对的,其部分代码如下:
% 生成同态滤波函数,中心在(m+1,n+1)
Homo = zeros(P, Q);
a = D0^2; % 计算一些不变的中间参数
r = rh-rl;
for u = 1 : P
for v = 1 : Q
temp = (u-(m+1.0))^2 + (v-(n+1.0))^2;
Homo(u, v) = r * (1-exp((-c)*(temp/a))) + rl;
end
end
%进行滤波
G = F1 .* Homo;
% 反傅里叶变换
gp = ifft2(G);
由于之前计算的fft结果没有中心化,所以进行滤波前需要对Homo进行反中心化,所以这里的代码也不对(这里是我错了,他代码前面有* (-1)^(i+j),有这个的话后面不需要ifftshift了)。
我们在看matlab—同态滤波的实现这篇文章的代码:
clear all
clc
I =imread('moon128.bmp'); % tun.bmp
figure(1),subplot(221),imshow(I); title('原图')
I=im2double(I); %转换数据类型为double型
[M,N]=size(I);
P = 2*M; Q = 2*N;
I2 = zeros(P,Q);
for i = 1:M
for j =1:N
I2(i,j) = I(i,j); %对图像进行填充
end
end
figure(1),subplot(222),imshow(I2);title('填充后的图像')
I2=log(I2+1); %取对数
FI=fft2(I2); %傅里叶变换
rL=0.25;
rH=2.2; % 可根据需要效果调整参数
c=2.0; %锐化参数
D0=20;
n1=floor(P/2);
n2=floor(Q/2);
for u=1:P
for v=1:Q
D(u,v)=sqrt(((u-n1).^2+(v-n2).^2)); %频率域中点(u,v)与频率矩形中心的距离
H(u,v)=(rH-rL).*(1-exp(-c.*(D(u,v)^2./D0^2)))+rL; %高斯同态滤波
end
end
H=ifftshift(H); %对H做反中心化
I3=ifft2(H.*FI); %傅里叶逆变换
I4=real(I3);
I5 =I4(1:M, 1:N); %截取一部分
I6=exp(I5)-1; %取指数
figure(1),subplot(223),imshow(I6,[]);title('同态滤波增强后')
个人觉得这个比较接近正确的结果了,但是我觉得还是有点问题,im2double函数会将图像数据归一化到【0,1】之间,和大部分的实现方式都不同。而且这个时候如果避免log后面参数为0,也不易加上1了,数量级太大了,加上0.0001之类的就可以了。
再找一篇文章的代码:同态滤波用于光照不均匀校正,这里的贴的效果也不错,代码如下:
clear all;
[filename,pathname]=uigetfile('*.*','选择图像文件');%通过浏览文件夹来读取图片
if isequal(filename,0) %判断是否选择
msgbox('没有选择任何图片');
else
image=imread(strcat(pathname,filename));%获取图像路径path,然后读取图片file
end
figure();subplot(2,2,1);
imshow(abs(image));
title('原始图像');
img=im2double(image); %转换图像矩阵为双精度型
lnimg=log(img+0.000001); %取对数
Fimg=fft2(lnimg); %傅里叶变换
P=fftshift(Fimg); %将频域原点移到图像中心;
[M,N]=size(P); %返回的行数和列数在P作为单独的输出变量
subplot(2,2,2);imshow(uint8(abs(P)),[]);title('滤波前的频谱图像');
%显示无符号8位数,即256级的灰度图像
x0=floor(M/2);
y0=floor(N/2);%表示将向量M和N每个元素与2作除法后取整
%同态滤波参数设置
D0=100;%截止频率
c=1.50;%锐化系数
Hh=0.5;Hl=2; %Hh<1,Hl>1,Hh为高频增益,Hl为低频增益,
%通过改变这两个参数,得到不同的滤波效果
for u=1:M
for v=1:N
D(u,v)=sqrt((u-x0)^2+(v-y0)^2);%点(u,v)到频率平面原点的距离
H(u,v)=(Hh-Hl)*(1-exp(-c*(D(u,v)^2/D0^2)))+Hl;%同态滤波器函数
end
end
hImg=Fimg.*H(u,v);%滤波,矩阵点乘
Q=fftshift(hImg);%傅里叶逆变换
subplot(2,2,3),imshow(uint8(abs(Q))),title('滤波后的频谱图像')
gImg=ifft2(hImg);%反傅立叶变换
Y=exp(gImg); %取指数
J=im2uint8(Y);%转换图像矩阵为无符号8位数,即256级的灰度图像
subplot(2,2,4),imshow(J),title(' 滤波后的增强图像')
这里的代码很明显的Hh还比Hl小,我是在搞不懂作者这里是怎么考虑的,同样的道理少了反中心化那一步。
通过以上代码,我们发现有的代码在做FFT变换前会将图像扩大一倍,比如这个matlab的网站中关于同态滤波也提到了2倍尺寸:https://blogs.mathworks.com/steve/2013/06/25/homomorphic-filtering-part-1/,虽然说得很有道理,但是经过测试,我觉得真的有必要吗,又占内存又减低了速度。
综合各篇文章的代码,通过实验我整理后的matlab代码如下:
% 同态滤波器
% ImageIn - 需要进行滤波的灰度图像
% High - 高频增益,需要大于1
% Low - 低频增益,取值在0和1之间
% C - 锐化系数
% Sigma - 截止频率,越大图像越亮
% 输出为进行滤波之后的灰度图像
function [ImageOut] = HomoFilter(ImageIn, High, Low, C, Sigma)
Img = double(ImageIn); % 转换图像矩阵为双精度型,不会改变数据本身
[Height, Width] = size(ImageIn); % 返回的行数和列数
CenterX = floor(Width / 2); % 中心点坐标
CenterY = floor(Height / 2);
LogImg = log(Img + 1); % 图像对数数据
Log_FFT = fft2(LogImg); % 傅里叶变换
for Y = 1 : Height
for X = 1 : Width
Dist= (X - CenterX) * (X - CenterX) + (Y - CenterY) * (Y - CenterY); % 点(X,Y)到频率平面原点的距离
H(Y, X)=(High - Low) * (1 - exp(-C * (Dist / (2 * Sigma * Sigma)))) + Low; % 同态滤波器函数
end
end
H = ifftshift(H); % 对H做反中心化
Log_FFT = H.* Log_FFT; % 滤波,矩阵点乘
Log_FFT = ifft2(Log_FFT); % 反傅立叶变换
Out = exp(Log_FFT)-1; % 取指数
% 指数处理ge = exp(g)-1;% 归一化到[0, L-1]
Max = max(Out(:));
Min = min(Out(:));
Range = Max - Min;
for Y = 1 : Height
for X = 1 : Width
ImageOut(Y, X) = uint8(255 * (Out(Y, X) - Min) / Range);
end
end
end
以上代码只针对灰度图像。
第一,我们没有将图像扩大2倍,实践证明不需要。第二,我们没有把图像归一化,如果使用归一化的代码,同样的参数会有不同的效果。第三,必须对H做反中心化处理,如果不对H反中心化,就要对FFT的结果进行中心化,此时代码如下所示:
function [ImageOut] = HomoFilter(ImageIn, High, Low, C, Sigma)
Img = double(ImageIn); % 转换图像矩阵为双精度型,不会改变数据本身
[Height, Width] = size(ImageIn); % 返回的行数和列数
CenterX = floor(Width / 2); % 中心点坐标
CenterY = floor(Height / 2);
LogImg = log(Img + 1); % 图像对数数据
Log_FFT = fft2(LogImg); % 傅里叶变换
Log_FFT = fftshift(Log_FFT);
for Y = 1 : Height
for X = 1 : Width
Dist= (X - CenterX) * (X - CenterX) + (Y - CenterY) * (Y - CenterY); % 点(X,Y)到频率平面原点的距离
H(Y, X)=(High - Low) * (1 - exp(-C * (Dist / (2 * Sigma * Sigma)))) + Low; % 同态滤波器函数
end
end
Log_FFT = H.* Log_FFT; % 滤波,矩阵点乘
Log_FFT = ifftshift(Log_FFT);
Log_FFT = ifft2(Log_FFT); % 反傅立叶变换
Out = exp(Log_FFT)-1; % 取指数
% 指数处理ge = exp(g)-1;% 归一化到[0, L-1]
Max = max(Out(:));
Min = min(Out(:));
Range = Max - Min;
for Y = 1 : Height
for X = 1 : Width
ImageOut(Y, X) = uint8(255 * (Out(Y, X) - Min) / Range);
end
end
end
算法使用场合及参数配置说明:
(1)、光照不均匀图像的均匀化。




要实现此种效果建议的参数配置如下:High = 2, Low =0.2, C > 1, 50<Sigma < 200;
(2) 偏暗图像的增强




要实现此种效果建议的参数配置如下:High = 2, Low =0.2, C = 0.1, Sigma = max(Width, Height);
以上是彩色的图,彩色图的处理方式有很多种,可以参考我以前所发的博文。
鉴于算法的这个特性,这个算法应该也可以应用在16位图像的HDR显示上,有空做做试验。
matlab的速度还是很慢的,我已经用C++结合SSE优化对上述过程进行了编码优化,其中的FFT使用了opencv的代码,目前opencv最新版本的FFT已经支持任意长度的序列了,但是为了速度,一般还是调用GetOptimalDftSize获取最佳的序列长度,然后用SSE优化一下其他的辅助处理,速度上对800*600的灰度图30ms左右。详见附件的SSE_Optimization_Demo的enhance菜单。

Demo下载地址:https://files.cnblogs.com/files/Imageshop/SSE_Optimization_Demo.rar


 浙公网安备 33010602011771号
浙公网安备 33010602011771号