5 月做题记录
懒得写题解了,就在这里放吧。。
不建议你们当成题解看,因为不是认真写的题解。
有的题会去补详细题解。
CF704D
题
先全染贵的那个颜色,然后看最多能染几个便宜的颜色。
建二分图,左边行,右边列,加个上下界限制,最大流就是最多能染几个便宜的颜色。
P3558
题
简单 DP
首先第一个数不会变,所以所有数下界 -1
其次弄出来大于 1 的数一定不优,如果弄出来个大于 1 的数,就往后看,发现 -1 还是要加两次,0 还是要加一次,这样一定不比把这个数搞成 1 优。
于是
\(dp_{i,j}\) 代表第 \(i\) 个数在第 \(j\) 个段,枚举这个和上一个直接转移。
P3554
题
先二分答案
首先每次肯定要染完所有儿子,然后剩余的次数相当于可以攒着以后用。
自上而下没法做,想到自下而上,反过来统计至少要从上面借来多少次数。
树形 DP,\(dp_u\) 代表 B 在 \(u\),这时 \(u\) 的整棵子树至少需要再染几个点(\(u\) 已染色) A 才能赢。
B 是可以往任意一个地方走的,转移的时候要求和,不是取最大值。
CF1137C
题
\(d\) 很小,不同周每一天的情况又都是一样的,考虑分层图。
结合了分层图和强连通分量,还是第一次见到。
P2851
题
完全背包 + 多重背包
找零上界一定不超过 \(2\times \max v_i^2\)。
AGC020E
题
我是先想的如果没有 1 变 0 操作应该怎么做,明显是个区间 DP。
\(f_{i,j}\) 代表 \([i,j]\) 方案数,\(g_{i,j}\) 代表缩成一个括号(以及只有一个字符的情况,0 或 1)\(f\) 转移的时候枚举最后一个括号位置。\(g\) 转移就枚举区间长度 \(len\) 的约数(\(len\) 除外)把这些缩成一个括号。
这题 \(f\) 还是一样的转移方式,不过算 \(g\) 的时候不同了,需要转移自的 \(f\) 需要是所有截取部分 AND 起来的值,可能会产生新的字符串,所以 DP 状态里就记字符串而不是区间了,记忆化搜索即可。
这个东西看起来复杂度很大但其实是对的,首先 \(f\) 刷出来的 \(f\) 不用考虑,因为 \(f\) 刷出来的 \(f\) 刷出来的 \(f\) 一定都是原来 \(f\) 的字串,还只有 \(n\) 个。而 \(f\) 也会产生 \(g\),并且 \(f\) 的每一个子串都会产生一个 \(g\) 的计算,而 \(g\) 又会产生新的 \(f\),这些产生出来的 \(f\) 是必须全部重新算的。
但是每次产生出来的 \(f\) 长度至多是原来 \(g\) 的一半,三次 \(g\) 产生 \(f\) 操作以后,长度就必定 \(\leq 13\) 了。长度为 \(n\) 的 01串只有 \(2^n\) 个,当 \(n\leq 13\) 的时候这其实并不大。
所以我们只需要考虑 \(g\) 变 \(f\) 一次和两次的情况就行了,而且分成 \(f\) 的次数两次乘起来还得小于 8,不然就长度太小了。其实最后生成的串可以看作是最早的原串取了几个字串拼起来的,这里用两次操作长度都减半举例好了。
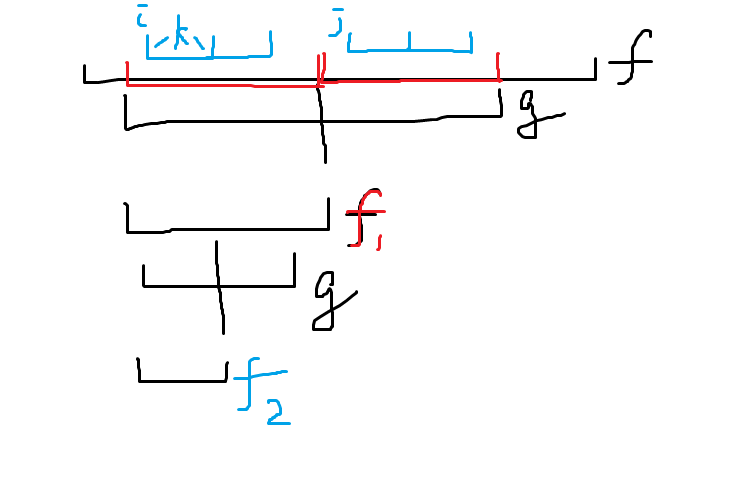
只用 \(i,j,k\) 就可以表示一个状态,那么状态数不会超过 \(n^3\)。
两次分别为分两段和分三段其实是一样的,状态数也只有 \(n^3\) 级别种。
实际值是远小于理论值的。
一共有 \(n^3+2^{\frac{n}{8}}\) 个状态,转移用时 \(n^2\),时间复杂度 \(O(n^5+n^2 2^{\frac{n}{8}})\)
AGC020D
ARC101E
ARC101F
题
出口情况固定的机器人先扔掉,剩下的要么在左边的出口出要么在右边。
算出来到左右的距离,分别为 \(x\) 和 \(y\),扔到坐标系上,找一条只往上或往右的折线,折线及其上方为从左边出,下方为右边出,\(dp_i\) 表示折线最后一个点经过的是 \(i\) 的总不同方案数,人为加上 \((0,0)\) 和 \((inf,inf)\)。
P3174
题
用求直径类似的方法跑一遍 DP 就行了,好像很简单。
P5385
题
对于森林,连通块数 = 点数 - 边数。
维护关于边加入时间的最大生成树(森林),求出来对于每一条边 \(e\) 最大的 \(l\) 使得只加入 \(l\) 以后 \(e\) 以前的边可以使得 \(e\) 连接两个连通块。加入这条边的如果生成森林里断了边,断掉的边就是 \(l\),没断边就认为 \(l\) 是 \(0\)。
后面的拿个主席树搞了就好了。
P4298
题
有向无环图最长反链板子。
第三问就强制选上这个点(删去与这个点有偏序关系的所有点)再求一遍最长反链,看看会不会挂掉。
CF590E
题
二合一了
前半部分直接跑 AC 自动机就 T 了,要只找到最近的有串的节点,然后一路路径压缩过去。
后面就是 DAG 最长反链
CF516D
题
这个 \(f_x\) 很奇怪,应该就是这题的切入点。
那个式子就是个尺取的形式吧,数据范围明示每次查询可以 \(O(n)\) 回答(不过实际上需要 dsu)。
然后就是要加点删点维护最大连通块,但是这个 \(f_x\) 性质没用到,一般看到这种东西应该能想到和直径有关,这题把直径的重点当根,\(f_x\) 就是小根堆,证明也很显然,就因为到一个点最远的点必然是直径的两端之一。
这样加点用并查集合并,而删点可以直接删,当前连通块大小 -1 即可。因为不会把一个连通块分成两个了。
CF603E
题
首先那个点度数的条件一看就是要转化,保证在保存现有的边的情况下,每一个连通块大小都是偶数就可以了,如果不满足可以删掉一些边,一定存在满足条件的方案。
用 LCT 维护最小生成森林,然后枚举现有的在森林中的最大边,能断则断,不能断更小的断掉也没意义。这个东西用堆维护就好了。
最后一步直接判最大值能不能删居然一直没想到,大概是遇到这种问题还没有这种意识。
AGC006B
题
写道水题放松一下。
首先 \(1\) 和 \(2n-1\) 不行,在倒数第二层一定就没了。
注意到三个数中位数的一个性质,如果某两数相等为 \(x\),则中位数一定为这个数 \(x\)。
那我们尽量在倒数第二层构造出来这样连续两个,发现这样一定能做到。
x
-xx
--xx-
---xx--
---lrxl--
// l 为任意小于 x 的数,r 为任意大于 x 的数。
// 如果 x=2,这四位就改成 rlxr 就行了。
AGC006D
题
直接确定顶部,感觉和 easy 有相似的思路。
观察那个两格宽的填满 x 的柱子,它一定是直接顶天的。
然后如果边上还没成柱子它还会向边上扩展一格,成柱子了就不行。
------0------
-----001-----
----|0011----
---||0011|---
--0|001011|--
-01001010111-
^^ ^^
0柱子 1柱子
但这样还是没法做,因为柱子太难形成了,没法快速判断。
这里继承上面的思路,二分答案,这样所有数都改成 lxr 了。
这样看起来会有问题,我们把二分答案的条件改成答案是否 \(\leq mid\) 就好了,这样所有数都只剩下 lr,我们只要看 l 的柱子和 r 的柱子哪个里中间近就可以了。
没有柱子的要特判。
AGC010B
题
先把总和不是一次减的倍数的判掉。
这个东西一看就没法直接做,一开始我考虑的是哪几个位置分别作为几次 5 的位置被减。
这个 1 2 3 4 5 (1) 差分完就变成 _1_1_1_1_-4(_) 了,感觉很可做,算出来一共减掉了几次,就能求上面说的那个东西了,负数和非整数判掉即可。
AGC021D
题
正串和反串会同时修改是比较麻烦的地方,但是这也让我们想到了一个特性。
- 给定 \(i,j\),正串的前 \(i\) 个和反串的前 \(j\) 个的 LCS,等于正串的后 \(j\) 个和反串的后 \(i\) 个的 LCS。
设 \(dp_{i,j,k}\) 表示正串的前 \(i\) 个和反串的前 \(j\) 个的 LCS。
答案就是 \(\max_{i=0}^n{2\times dp_{i,n-i,k}}\)。
但这样并不对,显然答案有可能为奇数所以不对。
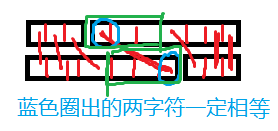
前半部分不一定匹配到最后了,中间那部分(短串最远的匹配处到蓝圈的位置处,绿色区域)如果不是空,一定至少能产生 1 的贡献。但是如果不是像图中蓝色圈出的字符一样,是 \(i\) 和 \(n-i+1\) 的配对产生贡献,这个贡献一定可以在 \(i\) 为其他位置时被算进去,只有蓝圈这样的配对是不行的,因为 \(i\) 向右移动同时 \(n-i+1\) 向左移动,它们不会同时出现在分割线的一边。解决方法也很简单,答案加入这个就行了(只删掉一个一定比删掉不止一个优)
\(\max_{i=0}^{n-1}{2\times dp_{i,n-i-1,k}}+1\)
P4197
题
想办法把那两个条件解决掉
从点 \(v\) 开始只经过困难值小于等于 \(x\) 的路径 \(\to\) Kruscal 重构树
所能到达的山峰中第 \(k\) 高的山峰 \(\to\) 主席树
对 dfs 序建主席树就行了,最后能访问的点一定是一整个子树,在dfs 序上是连续的。
CF685C
CF568C
题
一眼 2-SAT,字典序最小就贪心,然后全是细节。
根据贪心从左到右逐位考虑,虽然看起来后面对前面会有限制,但是通过 2-SAT 转成前面对后面的限制了。如果前面每一位都是顶上界的(和给定字符串相等)首选就是对应字符串的那一位,否则就是 'a'。
但这样很可能是不合法的,也就是说后面不管怎么填也没法合法,不过这个并不难判断,有以下两种情况,假设目前判断第 \(i\) 位能不能填给定字符。
- 前 \(i\) 位决定后,后面出现既必须为 'V' 又必须为 'C'
- 前 \(i\) 位决定后,前面仍然顶上界,假设第 \(i+1\) 到 \(i+k\) 位选 'C' 还是选 'V' 已经确定,而 \(i+k+1\) 位没确定或者这位已经是字符串以外的位置,并且这一段无论怎么选也选不出字典序比给定字符串那段大的字符串(比如 'V' 最大选 'b',\(i+1\) 位只能选 'V',而给定字符串要求 'c')
第二种有点复杂
然后看最优情况下不行的话,还有什么选项可以填,会决定一个位置对后面是否有解的影响的,无非就两个。
- 前 \(i\) 位是否顶上界
- 第 \(i\) 位是 'C' 还是 'V'
四种情况枚举一下,即可,如果前面不顶上界了后面就不可能再顶了,注意字典序从小到大,我这里实现的比较复杂。
P5155
题
挺妙的一道题。
从有一些点出发,按最优策略走的话,如果跳下,期望得分比继续走大,那么就一定选择跳下。
其他点出发,一定是走到它左边的第一个上一类点或者它右边的第一个上一类点,然后跳下,左边还是右边的概率可以算出来。
选择跳下的点构成一个凸包。
\(0\) 和 \(n+1\) 是强制跳下,也把它们也加入凸包。



