[算法笔记] 双连通分量
由于想把文章写的短一点，所以把割点和这篇分开了。
在阅读本文之前，请先阅读割点与割边
边双联通分量 Edge Double Connected Component
先讲边双是因为它比点双简单
性质
先给定义：不存在割边的极大双连通子图
（再加入任何一个/一些点后，它都会不连通或出现割边，不再是 e-DCC）
画张图吧，好理解
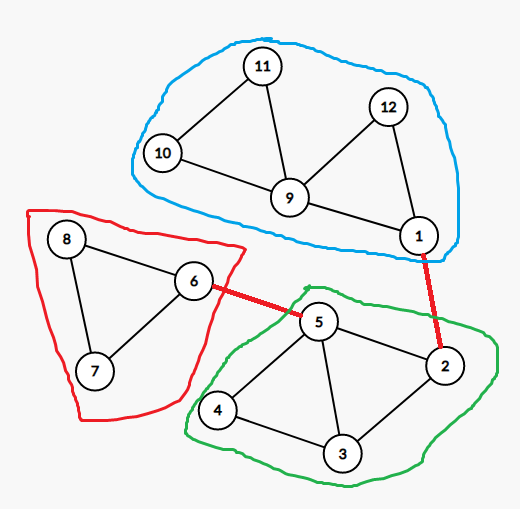
红边是割边，圈出来的是三个双联通分量。
性质：
- 边双连通分量中任意一条边都包含在至少一个简单环中
这条性质也是边双的充要条件。
分别证明，首先若该性质满足，那么删去任意一条边不会影响这个环中点之间两两可达性，这样任意一条边都不为割边了，必为边双。
然后，若图为边双连通图，反证，如果 \((u,v)\) 不包含在任意一个简单环中，断掉该变后，\(u\) 没有路径可以到达 \(v\)，图不再连通。
但是边双中并不一定包含一个经过所有点的简单环，点双也是，反例如下。
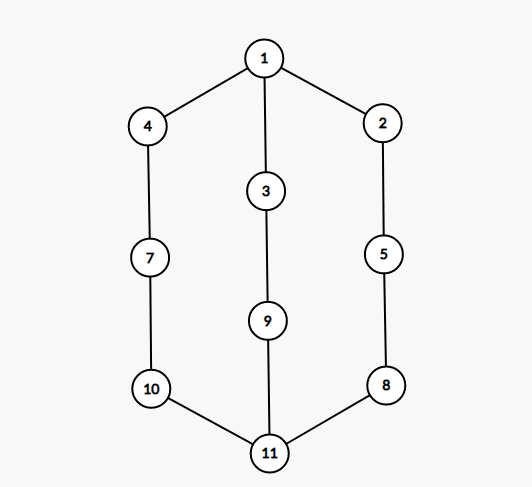
求法
把所有割边断掉，剩下每个连通块各为一个边双连通分量。
边双缩点：边双树
就像强联通分量缩点一样，我们可以把每一个边双缩成一个点来处理一些问题，然后这些点之间由原来的割边相连形成了一棵树。
最后得出一定是一棵树（森林），如果不是树，那就有环，环就是个边双。
就像强连通分量分解把一般有向图变成了有向无环图一样，我们把无向图的问题转到了树上，更好处理了，同时也保存了原来无向图的信息。
例题：codeforces 555E Case of Computer Network
题
首先缩点成边双森林，定根，每条路径拆成向上和向下两部分，如果有一条边既要向上又要向下，那就无解了。
这个用树上差分实现，维护点信息对应其父边信息。
这里简单地讲一下如果要求具体方案的做法。
对于割边，看覆盖这条边的路径是向上还是向下的即可。
边双经过定向可以成为一个强连通分量。
无向图的 dfs 树只有返祖边和树边，没有横叉边。
把边双单独拿出来建个 dfs 树的话，树边向儿子，返祖边向祖先连即可。
一路往下走到叶子之后，一定会存在一条路能够回到根，否则这个叶子就不会在边双里面了（由于没有横叉边，它能走到的所有点是一棵完整的子树，且该子树根不是树的根），到根以后，就可以往下走到任何一个节点了。
点双联通分量 Vertex Double Connected Component
其实和前者非常的相似
性质
先给定义：不存在割点的极大双连通子图
画张图吧，好理解
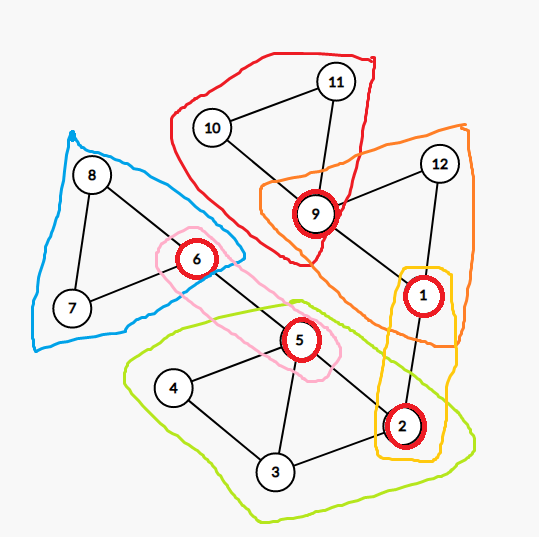
性质：
- 点双连通分量中任意两点都同时包含在至少一个简单环中
等价于两点间存在两条不相交（没有公共点）的路径。
这条性质也是点双的充要条件。
若任意两点间存在两条不相交的路径，那么不存在同时在两条路径上的点，两点一定能互达，所以图中不存在割点，即图为点双连通图。
若图为点双连通图，继续反证，假设存在两点 \(u,v\) 它们不同时处于任一简单环中，如果这两点间只有一条路径，那么必存在割点，如果有大于等于两条路径，这些路径若不相交于 \(u,v\) 以外的点就一定会成环，所以这些路径一定会交于某一点，这样这个点就成为了割点，与点双连通图矛盾。
- 一个点双中的两不同点之间一定存在简单路径，使得该路径经过在同一个点双内的另一点
- 两点双连通分量之间如果有公共点，这个公共点一定是唯一的，且一定是割点
注意下面这两个图是符合定义的，但是会不符合性质，是特例。
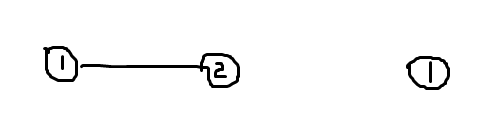
求法
如果仿照上面的做法，把所有割点断掉，剩下每个连通块各为一个点双。
但这是错的，因为割边不包含于任一边双中，但是割点一定包含于至少两个点双中。
这个做法相对比较复杂。
还是用 Tarjan 算法，维护一个栈，对整张图做 dfs。
- 若一个节点第一次被访问，将其入栈
- 在割点处理过程中，在处理 \(u\) 的儿子 \(v\) 时，如果遇到 \(dfn_u\leq low_v\)，则从栈顶不断弹出节点直到 \(v\) 被弹出为止（\(v\) 要弹出）这些点和 \(u\) 一起构成一个点双连通分量
注意到这里没有弹出 \(u\)，因此此时 \(u\) 是一个割点，计算它和它子树中节点组成的点双时不能弹出，因为它包含于不止一个双联通分量，只有在处理它某个祖先节点时，才会弹出这个节点，这样处理完它的子树的 v-DCC 后再处理和它祖先构成的 v-DCC 最后弹出，就可以计入所有 v-DCC 了。这个点作为割点，也是必定会包含在上面的那个点双里的（根节点除外）。
void tarjan(LL u,LL fa){
low[u] = dfn[u] = ++ ti;
stk[++ top] = u;
LL tot = 0;
for(LL i = hed[u];i;i = nxt[i]){
LL v = to[i];
if(!dfn[v]){
++ tot; tarjan(v,fa);
low[u] = min(low[u],low[v]);
if((u == fa && tot >= 2) || (u != fa && dfn[u] <= low[v])) cut[u] = 1;
if(dfn[u] <= low[v]){
bc ++; blk[bc].clear();
do{
blk[bc].push_back(stk[top --]);
}while(stk[top + 1] != v);
blk[bc].push_back(u);
}
}
else low[u] = min(low[u],dfn[v]);
}
}
圆方树
与边双树相对应。
在处理点双的问题时，往往会使用圆方树，将图的问题转化为树上问题，并很好的保留了原图的信息。
对每一个点双，建立一个方点，将这个方点与原来点双中的所有点相连，连成一个菊花图来处理，这样可以得出一棵树。（如果成环了，相应的，这个环也能缩成一个点双，所以必定是树）
借用 WC ppt 的一张图
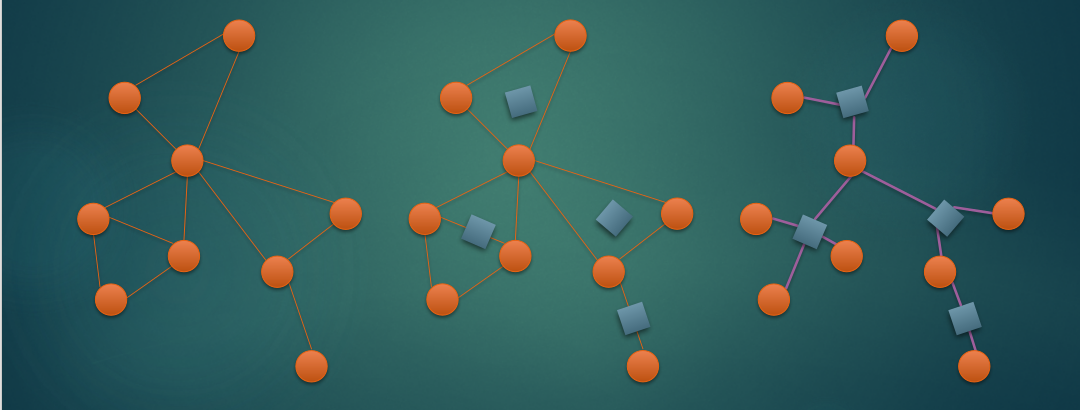
这超出了本文的讨论范围了，感兴趣的读者可以自行查询资料学习。
说白了，就是我不会啊
