[算法笔记] 割点与割边

一般用 Tarjan 算法解决
桥和割边是一个东西

割点和割边

定义

若对于无向连通图的一个点 \(x\)，从图中删去这个点和与这个点相连的所有边后，图不再是连通图，则 \(x\) 为这个图的割点。
若对于无向连通图的一条边 \(e\)，从图中删去这条边后，图不再是连通图，则 \(e\) 为这个图的割边。

当然那张图可能本来就不连通，所以严格来说是把一个连通块断开了，改变了原来的连通块是否连通，是这个连通块的割点或割边。不过从总体来看，删除这个点或边还是改变了整张图的连通性。

无向图的 dfs 树

与有向图 dfs 树类似。

任选一个点开始出发进行 dfs，保证每一个点只访问一次，把所有发生了递归的边标为树边，所有树边构成一棵树。
对应到树上，每一个点都只有一个父亲节点，就是第一次访问这个点时对应的那个点（第二次访问时就直接跳过这个点了）。
还是来张图（红色为树边）：

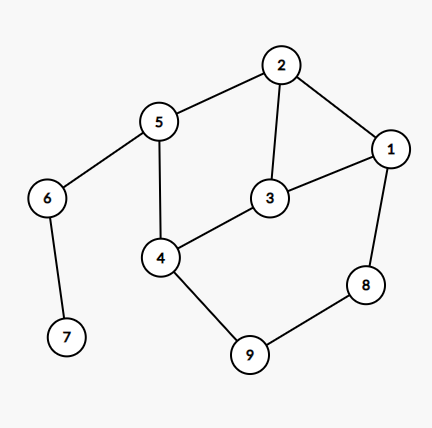
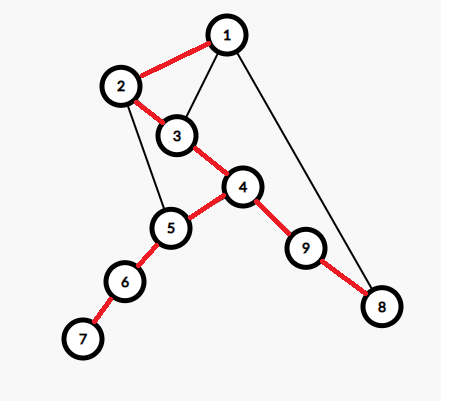
然后将边分为两类，树边和返祖边，返祖边连接了一个点和它的一个祖先。
注意，与有向图不同，无向图 dfs 树没有横叉边。

时间戳 dfn 与追溯值 low

在 dfs 的过程中，按每一个节点第一次被访问的顺序，给每个点标上一个数字，代表是第几个被第一次访问的，记为时间戳。

\(u\) 的追溯值指的是 \(u\) 的子树中所有点 和 从 \(u\) 的子树中的点通过仅一条返祖边可以到达的点的时间戳的最小值。

下图中，黑色数字代表每个点的 dfn，红色数字代表 low。

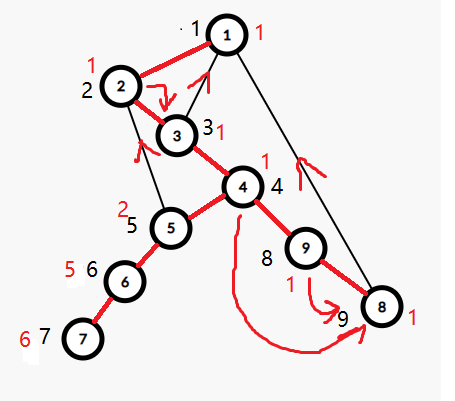
割边的判定

首先注意到，割边只可能是树边，不可能是返祖边。
假设 \(u\) 是 \(v\) 的父亲，如果从 \(v\) 的子树中任意一点出发都不能到达 \(u\) 或 \(u\) 的祖先，也就是时间戳比 \(x\) 小的点（不要管那些点的其它子树，由于没有横叉边，它们只能通过先走到 \(u\) 或 \(u\) 的祖先再往下走到达），那么删去这条边后，\(v\) 的子树就与图的其它部分断开了。
判断条件就是 \(low_v>dfn_u\)

否则的话，\(v\) 就有至少两条路到达 \(u\)，一条是 \((v,u)\) 另一条是先向下走到子树中某个点，再走返祖边，再向下走到 \(u\)。

void tarjan(LL u,LL fe){
	dfn[u] = low[u] = ++ dfc;
	for(LL i = hed[u];i;i = nxt[i]){
		LL v = to[i];
		if(!dfn[v]){
			tarjan(v,i);
			low[u] = min(low[u],low[v]); // v 在 u 的 子树中，所以这里取 low
            // 搜索完 v 的子树，找出 v 的子树的 low 再取最小值来求出 u 的 low
			if(low[v] > dfn[u]) bri[i] = bri[i ^ 1] = 1;
		}
		else if(i != (fe ^ 1)) low[u] = min(low[u],dfn[v]);
        // 这条边是返祖边，所以取 dfn，这里一定不能取 low
        
        // 存边的时候，把 (u,v) 和 (v,u) 分别存为 2,3/4,5/6,7/... 通过 ^1 就是另一条边的编号
        // 算 low 的时候不能把父亲节点的 dfn 算进去
        // 同时，这样可以处理重边的情况
	}
}

割点的判定

思想类似。
若 \(u\) 是割点，那么只要存在 \(u\) 的一个子节点 \(v\)，使得 \(low_v \geq dfn_u\)，则 \(u\) 是割点。
相应的，删去 \(u\) 后 \(v\) 无法到达 \(u\) 或 \(u\) 的祖先了

还有一个特殊情况，就是对于搜索树的根，如果它只有 1 个儿子（通过树边与之直接相连的点），它不能成为割点，这里需要特判。

树的叶子节点由于没有儿子，也不会成为割点。

inline void tarjan(LL u,LL fa){
	low[u] = dfn[u] = ++ ti;
	LL tot = 0;
	for(LL i = hed[u];i;i = nxt[i]){
		 LL v = to[i];
		if(!dfn[v]){
			++ tot; tarjan(v,fa);
			low[u] = min(low[u],low[v]);
			if((u == fa && tot >= 2) || (u != fa && dfn[u] <= low[v])) cut[u] = 1;
            // dfn[u] == low[u] 其实也对
		}
		else low[u] = min(low[u],dfn[v]);
        // 这里判定的时候取的是小于等于，所以可以无视父边影响
		// 重边也是没有影响的，因为我删除的是点
    }
}

应用之一：双连通分量