[算法笔记] 并查集

这好像是很久以前写的了，那时候没发..
updated 2019.11.30 填坑+补充

并查集是一种用于处理一些不相交的集合的合并与查询问题的树形数据结构
能够将两个集合合并 或者查询某个元素处于哪个集合中

预处理

首先并查集维护的是一个有根树森林
森林中每一棵树代表一个集合（相当于连通块）
一棵树中所有点的祖先都是相同的（即树根）所以查询两个点是否在同一棵树中可以等价为查询它们的祖先是否相同
我们要高效维护祖先信息

先考虑朴素算法 首先我们对每一个点存下它父亲的值 祖先就是不断找父亲直到顶就可以了
为了判断一个点是祖先节点并且方便处理 我们把祖先节点的父亲节点设置成自己
于是父亲是自身的点都是祖先节点

一开始每一个点都自己组成一个连通块(一棵树)

记\(f_i\)为\(i\)的祖先

for(int i = 1;i <= n;i ++) f[i] = i;

合并与查询

可以视为是在 对两棵树的根连边 和 树上找祖先 的过程

查询

先考虑朴素做法
对于一个元素 不断找它的父亲节点 直到找到祖先节点为止 就可以了
这个点就是该节点所在树的根 相当于所在集合的编号
祖先节点的 f 是它本身

如果两个元素的祖先节点相同 它们就在同一个集合中了

int find(int x){
	if(x == f[x]) return x;
	return find(f[x]);
}// 查询祖先 采用递归方式实现
char judge(int x,int y){
	if(find(x) == find(y)) return 'Y'; // 在同一个集合内
	return 'N';
}

合并

先找到待合并两个点的祖先
将一个祖先的父亲设为另一个祖先就可以了
必须要祖先，树里随便抽一个点出来是不行的
注意这里被合并的祖先的子树中所有点的祖先信息都还没有更新为另一个祖先
所以每一个想调用一个元素的祖先信息时 一定要再把它做一遍查询找出它祖先的值 再去调用

void union(int x,int y){
	x = find(x); // 找祖先
	y = find(y);
	f[x] = y; // f[y] = x 也行 并起来就可以了
}

不过这个算法显然可以被卡成单次查询\(O(n)\)的
所以我们需要优化

优化

虽然说是优化 但是前面的算法不优化复杂度太大了
所以优化是必须的

路径压缩

由于只需要祖先信息 而且只有合并没有拆分
所以对于一个元素 它的祖先是它的父亲 还是它父亲的父亲 其实是不重要的
所以我们可以在查询到一个点的祖先的时候 把这个点到祖先路径上所有点的 父亲节点编号(即\(f_i\)) 直接改成祖先
由于上面的过程是递归实现的 路径上每一个点都可以在找到祖先后修改父亲节点
相信还是看图更好理解

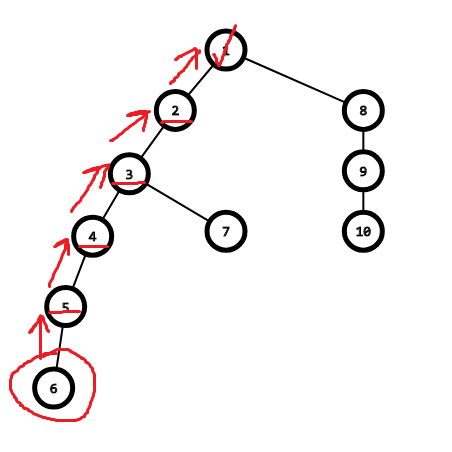
找祖先

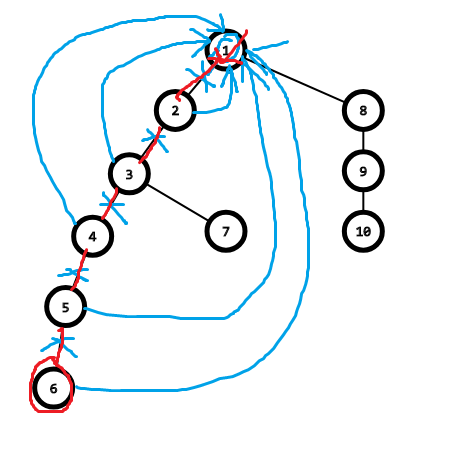
改父亲节点编号

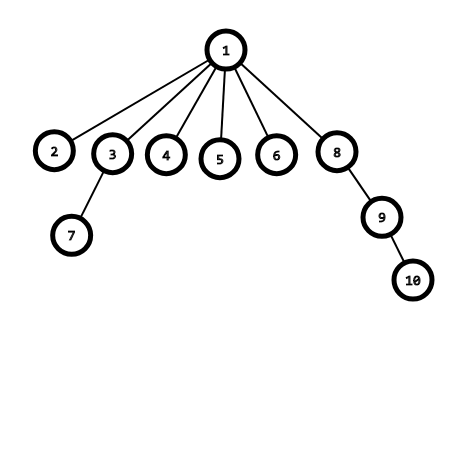
代码也很简单 就加了五个字符

int find(int x){
	if(x == f[x]) return x;
	return f[x] = find(f[x]);
}

时间复杂度(m次询问):
最坏\(O(mlog\ n)\)
平均\(O(m\alpha (n))\) 这个东西很小 可以当成常数了

启发式合并

可支持撤销
路径压缩是保存了祖先关系而破坏了点的父子关系 所以不能够撤销
而启发式合并不会
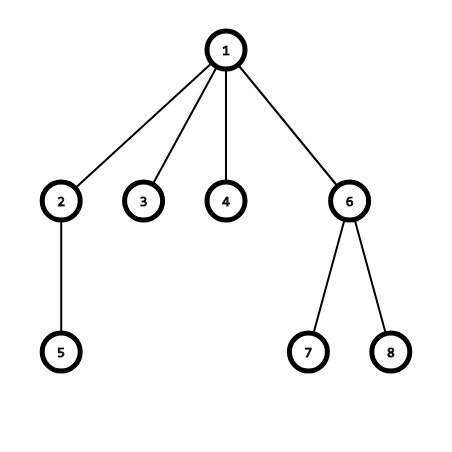
启发式合并就是每一次合并都是把小的集合(含元素少)并到大的集合里面去
如果一开始所有集合都是只有一个元素的
那么经过这样的合并后 从根节点往下走 每走一步子树大小至少减半
这样可以保证查询复杂度

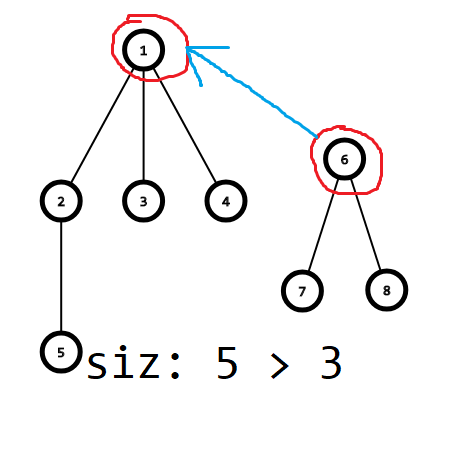
// siz记录子树的大小 初始化为1
void unionSet(int x, int y) {
	x = find(x); y = find(y);
	if(x == y) return;
	if(siz[x] > siz[y]) swap(x,y);
	f[x] = y; siz[y] += siz[x];
}

撤销的时候把之前连上去的那条边删掉就行了(把对应那个点的祖先改成自己)
树的结构没有改变 所以可行
时间复杂度\(O(m\log n)\)

种类并查集/扩展域

拿这题举例子了:NOI2001 食物链
这里同类关系可以简单的用并查集解决
但是天敌和猎物的关系就不能处理

所以对每一个生物\(i\)建立三个元素 分别代表\(i\)是生物\(A,B\)还是\(C\)
记作\(i-A,i-B,i-C\)
在合并的过程中 我们需要使得对于任意一个连通块 该连通块内所有元素要么同时满足 要么同时都不满足
同一个集合内的元素可以互相推出

合并之前判断一下有没有矛盾
如果\(x,y\)为为同类则合并\(x-A,y-A;x-B,y-B;x-C,y-C\)

如果此时\(x-A,y-B\) 或 \(x-B,y-A\)已在同一连通快内 代表\(x\)和\(y\)是天敌和猎物的关系 就不可能是同类了 于是产生矛盾
其实只需要判断A,B即可 如果\(x-A,y-B\)在同一连通块内，\(x-B,y-C\)必定也在

如果\(x\)吃\(y\)则合并\(x-A,y-B;x-B,y-C;x-C,y-A\)(因为A吃B B吃C C吃A)
这时候如果发现之前\(x,y\)就是同类或者\(y\)吃\(x\) 那么就矛盾了

这里用\(i,i+n,i+n+n\)表示\(i-A,i-B,i-C\)

// 同类合并
if(find(x) == find(y + n) || find(y) == find(x + n)) ans ++;
else{
	f[find(x)] = find(y);
	f[find(x + n)] = find(y + n);
	f[find(x + n + n)] = find(y + n + n);
}
// x吃y
if(find(x) == find(y) || find(x + n) == find(y)) ans ++;
else{
	f[find(x)] = find(y + n);
	f[find(x + n)] = find(y + n + n);
	f[find(x + n + n)] = find(y);
}

带权并查集

其实就是给森林中的每一个点都赋值 保存下这个点的信息 以及 它到父亲节点的边的信息
然后在合并的时候(路径压缩)改变这些值 查询的时候查询值 就行了
拿这题举例:NOI2002 银河英雄传说

这里记\(b_i\)为\(i\)点所在连通块大小
\(s_i\)为\(i\)点到这个点所在树的根的距离
由于路径压缩的过程中树的结构发生了改变
所以要随时更新这两个值

int find(LL x){
	if(x == F[x]) return x;
	int tmp = F[x];
	F[x] = find(F[x]);
	s[x] += s[tmp];
	b[x] = b[F[x]];
	return F[x];
}
// 预处理
for(int i = 1;i <= 30000;i ++){
	F[i] = i; b[i] = 1; s[i] = 0;
}
// 合并
fx = find(x); fy = find(y); F[fx] = fy;
s[fx] += b[fy];
b[fy] = b[fx] + b[fy]; b[fx] = b[fy];
// 查询
fx = find(x); fy = find(y);
if(fx != fy) cout << -1 << endl;
else cout << abs(s[x] - s[y]) - 1 << endl;

总结

并查集作为一个能够维护 集合/连通块信息(大小/数量/...)/连通性 的高效数据结构 在实际题目中有用处很多 并且很容易实现 灵活性也不差
总之就是如果想到某处用并查集比较合适就用吧

虽然并查集能做的LCT都能做