[AGC020E] Encoding Subsets 题解

AGC020E

题

我是先想的如果 1 不能变 0 应该怎么做，明显是个区间 DP。
\(f_{i,j}\) 代表 \([i,j]\) 方案数，\(g_{i,j}\) 代表缩成一个括号（以及只有一个字符的情况，0 或 1）\(f\) 转移的时候枚举最后一个括号位置。\(g\) 转移就枚举区间长度 \(len\) 的约数（\(len\) 除外）把这些缩成一个括号。

这题 \(f\) 还是一样的转移方式，不过算 \(g\) 的时候不同了，需要转移自的 \(f\) 需要是所有截取部分 AND 起来的值，可能会产生新的字符串，所以 DP 状态里就记字符串而不是区间了，记忆化搜索即可。

这个东西看起来复杂度很大但其实是对的，首先 \(f\) 刷出来的 \(f\) 不用考虑，因为 \(f\) 刷出来的 \(f\) 刷出来的 \(f\) 一定都是原来 \(f\) 的字串，还只有 \(n\) 个。而 \(f\) 也会产生 \(g\)，并且 \(f\) 的每一个子串都会产生一个 \(g\) 的计算，而 \(g\) 又会产生新的 \(f\)，这些产生出来的 \(f\) 是必须全部重新算的。

但是每次产生出来的 \(f\) 长度至多是原来 \(g\) 的一半，三次 \(g\) 产生 \(f\) 操作以后，长度就必定 \(\leq 13\) 了。长度为 \(n\) 的 01串只有 \(2^n\) 个，当 \(n\leq 13\) 的时候这其实并不大。

所以我们只需要考虑 \(g\) 变 \(f\) 一次和两次的情况就行了，而且分成 \(f\) 的次数两次乘起来还得小于 \(8\)，不然就长度太小了。其实最后生成的串可以看作是最早的原串取了几个字串拼起来的，这里用两次操作长度都减半举例好了。

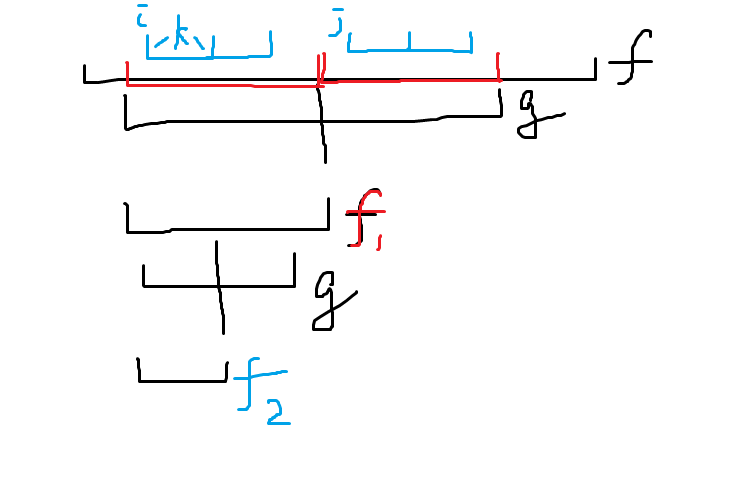
只用 \(i,j,k\) 就可以表示一个状态，那么状态数不会超过 \(n^3\)。
两次分别为分两段和分三段其实是一样的，状态数也只有 \(n^3\) 级别种。
实际值是远小于理论值的。

一共有 \(n^3+2^{\frac{n}{8}}\) 个状态，转移用时 \(n^2\)，时间复杂度 \(O(n^5+n^2 2^{\frac{n}{8}})\)

代码写得很丑（）

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <map>
#include <string>
using namespace std;
typedef long long LL;
const LL N = 998244353;

map <string,LL> mp[2];
string u;

LL f(LL id,string s){
	if(mp[id].find(s) != mp[id].end()) return mp[id][s];
	LL ret = 0,len;
	len = s.length();
	if(id){
		for(LL i = 0;i < len;i ++) ret = (ret + f(1,s.substr(0,i)) * f(0,s.substr(i,len))) % N;
		mp[id][s] = ret; return ret;
	}
	else{
		for(LL i = 1;i < len;i ++){
			if(len % i) continue;
			string t = "";
			for(LL j = 0;j < i;j ++) t += '1';
			for(LL j = 0;j < len;j += i){
				for(LL k = 0;k < i;k ++){
					if(s[j + k] == '0') t[k] = '0';
				}
			}
			ret += f(1,t); ret %= N;
		}
		mp[id][s] = ret; return ret;
	}
}

int main(){
	mp[0][""] = mp[1][""] = 1;
	mp[0]["0"] = 1; mp[0]["1"] = 2;
	mp[1]["0"] = 1; mp[1]["1"] = 2;
	cin >> u;
	cout << f(1,u) << '\n';
	return 0;
}