技巧瞎扯

先声明一下，这里基本只是说一下有这个东西，有这么回事，讲的确实很不详细吧，都是一笔带过，真正想体会可能还是要通过做题的过程。

好像很多都是烂大街了，那只能说我菜了。

不断更新

差分
二分答案
根号分治，分块

各种拆点
（出入点/分层图/...）

正难则反

找单调性

LCT 维护边删除时间的最大生成树

做题没思路的时候可以尝试先枚举一个东西然后看能不能做。

直接忽略 不合法 但是 造成的答案不可能比最优解更优 的转移，有时候会很难处理不合法的情况。

对于一堆多元组，考虑按其中某一个元素从小到大/从大到小排序。

常见：给一堆区间询问 \([l,r]\)，把所有询问按 \(r\) 从小到大排序。

先排序确定选取后这些元素的顺序，先将所有元素排序，再对这些元素做选取
确定顺序可以通过邻项交换排序
比较 在前面先任意放一些元素，后面的两个位置考虑 \(a\) 和 \(b\)，比较这种情况下 \(a\) 在前和 \(b\) 在前的代价，取其中更优的那个，这样可以推出一个比较公式，扔进 cmp 然后 sort 就行了，注意要满足严格弱序。

有的题如果想要有解，一定是必须满足一些性质的，不找出一些性质就做不了，可以先看什么时候无解，然后把这个性质找出来。

一些建图的题，如果建完图就不会了，可以看看图有什么性质，可能是平面图/二分图/..

一般而言，答案具有单调性可以把最优化问题二分答案转化为判断可行性问题。
对于一些判断可行性问题，条件是必须每个数都有配对之类的，可以变成最优化，求最多能配对多少，看这个最优情况是不是满的。

有些题可以先算出理论下界/理论上界，然后发现一定可以构造出一组可以达到这个理论界的方案。

\(dp_i\) 表示强制第 \(i\) 个满足 xxx 条件，前 \(i\) 个的 xxx，人为添加第 \(0\) 个和第 \(n+1\) 个。
枚举的时候枚举上一个强制满足条件的是哪个，假设这个是 \(j\)，\(j+1\) 到 \(i-1\) 的所有都不满足这个特殊条件。
这是做到不重复计数的一种方法
类似的：枚举第一个部分，1 号点所在的连通块的大小 ...
欧拉筛中每个数只会被最小质因子筛一次，也是相似的思想。

\(dp_i=\max\{dp_j+w(i,j)\}\)
\(dp_i=-\min\{-dp_j-w(i,j)\}\)
\((-dp_i)=\min\{(-dp_j)+(-w(i,j))\}\)

点对可以转成二维数点问题
（很多东西都能转成二维数点）

原先设计的状态中答案范围小时，把储存的答案作为 DP 状态的某一维重新设计状态

森林：联通块数 = 点数 - 边数

补图转化（独立集\(\leftrightarrow\)团）
独立集的补集是点覆盖，匹配的补集是边覆盖。
二分图最大匹配 = 最小点覆盖 = 点数 - 最大独立集 = 点数 - 最小边覆盖

01 矩阵快速幂 bitset 优化

曼哈顿距离拆开 \(dis_{i,j}=\max((+x_i+y_i)+(-x_j-y_j),(+x_i-y_i)+(-x_j+y_j),(-x_i+y_i)+(+x_j-y_j),(-x_i-y_i)+(+x_j+y_j))\)。
这样可以去掉绝对值，变成 max。

曼哈顿距离 \((x,y)\) 转切比雪夫距离 \((x+y,x-y)\)。
切比雪夫距离 \((x,y)\) 转曼哈顿距离 \((\frac{x+y}{2},\frac{x-y}{2})\)，切比雪夫距离是 \(\max(|x_i-x_j|,|y_i-y_j|)\)，有时候 max 不好处理，就可以这样去掉只留下绝对值。
这里相当于坐标系转换，每个点都要做这样的变化。

一些树上点 大量点对之间的路径 问题，可以转为分别考虑每条边的贡献，本来是平方的，现在变成了线性。

一些奇怪的哈密顿路径问题，换成哈密顿回路减掉一条边，回路的情况一般都会很好做。

枚举非树边替换最小生成树上的边（次小生成树 等）

状压 DP 枚举子集 T=(T-1)&S，初始化 T=S。
S 为全集，T 可以枚举到 S 的所有子集

（可删堆）开两个堆，其中一个保存要删除的数，每次取堆顶前比较两堆堆顶，一样就弹出，弹到空或不等为止。
还有一种比较简单的，就直接给要删掉的数打个标记（有点像延迟标记），想要出堆时如果堆顶是带标记的数，就删掉找下一个堆顶，然后把删除标记弄掉（有重复数就标记 +/- 1），对于栈等其它数据结构会用到。

时光倒流（删边->加边）
线段树对时间分治

\(\gcd(a_1,a_2,\cdots ,a_n)=\gcd(a_1,a_2-a_1,a_3-a_2,\cdots ,a_n-a_{n-1})\)。差分维护

边的信息下放到点上，变成处理点的信息（QTREE1）
点的信息移动到父边，变成处理边的信息（根的父亲加虚点）（QTREE6）
因为每一个点只有一个父边（除了根）

用矩阵维护图上任意两点间可达性/距离，矩阵乘法相当于走一步路，用矩阵快速幂就能加速。

冒泡排序交换次数 = 逆序对数
一轮交换的影响：记录第 \(i\) 个位置，它之前比它大的数的个数，每个位置的值加起来就是逆序对数。整体前移，然后所有非零数减一 \(\max(x-1,0)\) 个。

4 1 5 3 2
0 1 0 2 3
1 4 3 2 5
0 0 1 2 0 (1 0 2 3 0-> 0 0 1 2 0)
1 3 2 4 5
0 0 1 0 0
1 2 3 4 5
0 0 0 0 0

路径异或一个环得到另一条路径（这条路径中可能有走了两次的边，这些边贡献为 0）

一类状压DP题，状态代表一个集合，\(dp_i\) 代表已经选择了 \(i\) 代表的集合 中的数时，最小的代价。转移就是枚举一个数加入集合，计算 集合内的数，加入的数，和其它未加入集合的数在这次操作中会产生的贡献。

树剖换根，并不是真的换根，查链不变，查子树时分类讨论，查询点在一开始建好的树的根和题目要求的根的链上时，取查询点不包含题目要求的根的所有子树信息即可，这其实就是两个部分信息并起来。否则照常。

树形背包，处理第 \(i\) 个子树的时候，容量第一维枚举前 \(i-1\) 个子树的大小之和这里面取几个，第二维枚举这个子树中取几个，这样复杂度是 \(O(nk)\)，可以看作每一对点至多被选取了一次，是在它们的 LCA 处的（01 背包两维都要倒序）。

\(1\times 2\) 的覆盖问题，把棋盘黑白相间染色，覆盖的一定是相邻的一黑一白。

实现所有数 +1 : 可以从低位往高位建 0/1Trie
进位就是 swap 两个子树，然后出现进位的那个子树继续 swap 两个子树，一直到底，树深度是 \(\log W\) 的。

随机一个排列，指定其中两个数 \(a,b\)，\(a\) 在 \(b\) 之前的概率一定是 \(\frac{1}{2}\)，对于每一个 \(a\) 在 \(b\) 前的排列，把它 reverse，就对应一个 \(b\) 在 \(a\) 前的。（排列总数一定是偶数）

带插入的块状数组，每做 \(\sqrt{q}\) 次操作就暴力重构，可以保证复杂度。（这种数据结构好像还挺好用的）

如果发现树的高度不大（或者两点间需处理的距离不大，这样需要枚举的 LCA 也很少），可以枚举 LCA 去解决某些问题。

一棵树上所有关键点形成的极小连通子树的边权和：先把所有点 \(x_i\) 按 dfs 序顺序排序，答案为 \(\frac{\sum_{i=1}^{n-1}dis(x_i,x_{i+1})+dis(x_1,x_n)}{2}\) （dis 为树上两点间距离）

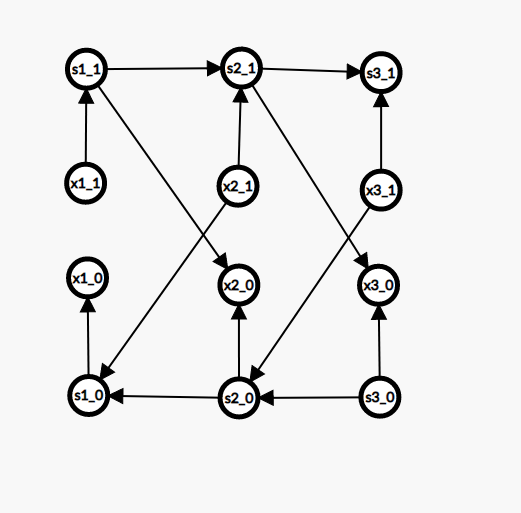
2-SAT 强制选一个数或不选：连一条边 \(\neg x\to x\) 或 \(x\to\neg x\)。

n 个元素中最多选择一个：2-SAT 前缀优化
（xa_b 代表第 x_a 为 0/1，sa_b 代表前 a 个元素中是否有 1）

对集合哈希，可以用于判断两集和是否相等
\(\prod{a_i+D}\)
在值域较小时，给值域中每个数赋予一个较大的权值，然后哈希值为\(\sum{W_k}\)
\(\sum{P^{a_i}}\)
这样可以实现可减性，然后求出区间哈希值。

大多数期望 DP 一般采用倒推更为容易，因为如果正推需要同时求出达到这一状态的概率

有时候需要用一个数组记录每个点是否访问过，并且要多次使用，如果只把这个数组作为 0/1，那每次使用都需要清空信息，直接把数赋值为当前操作的次数（第几次）而不是 1，这样就不用每次清空了。

条件是 要求两个数乘起来是完全平方/k 次方数 的题，就把每个数质因数分解然后每个质因子质数 mod k，然后每个数能配对的数就是唯一的了。

网格 -> 黑白染色 -> 二分图

\(n\) 个 \([0,1]\) 的随机实数的期望最大值是 \(\frac{n}{n+1}\)，期望最小值是 \(\frac{1}{n+1}\)。
这样可以直接用最大值最小值估计数量。
比如算有向无环图每个数后继个数。

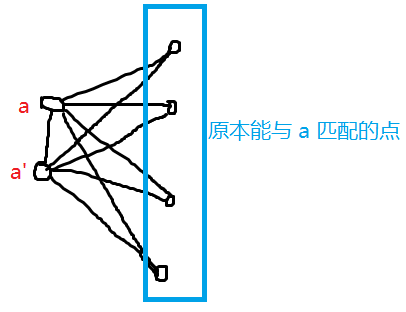
左边一个点必须匹配右边两个点才能形成几个匹配，把左边每个点都拆成两个点，如下建图然后做一般图最大匹配。
这样如果原本的 a 只选择了一个匹配，不如选新图中 a 和 a' 的匹配，如果原本的 a 选择了两个匹配，则新图中 a 和 a' 各匹配右边一个点。

树上两邻域的交还是邻域。