Tarjan算法强连通分量分解学习笔记

Tarjan算法有很多应用 还可以求 无向图的割点和桥 点双连通分量 边双连通分量 LCA 等

1.强连通分量

定义:强连通分量是一个点的集合 从任意一个点出发都可以到达集合中的所有点
也就是任意两点之间可以相互到达

画张图理解吧

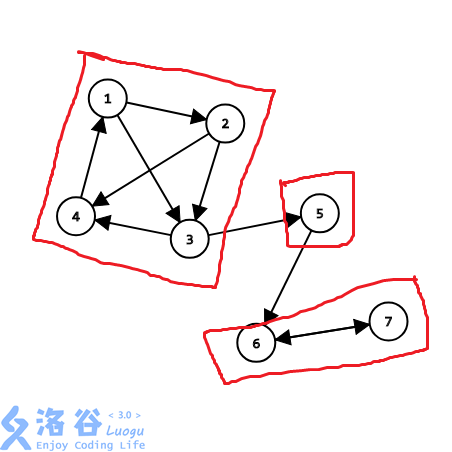
每一个用红线框起来的部分都是一个强连通分量
1 2 3 4可以互达 6 7可以互达
注意单个点{5}也是一个强连通分量

当然\(\{1,2\}\)也是一个强连通分量 但是我们缩点的时候由于\(\{1,2\}\)是\(\{1,2,3,4\}\)的子集 所以缩点时直接缩\(\{1,2,3,4\}\)了

如果我们把所有强连通分量都缩成一个点 该有向图就会成为有向无环图(DAG) 从而使得一些问题能够得以更好的解决

2.Tarjan算法实现强连通分量分解

首先将这个图从任意一个节点开始(这里从1开始了) 大法师(dfs)遍历
过程中遇到已经便利过的点就跳过

遍历顺序:1->2->4->3->5->6->7

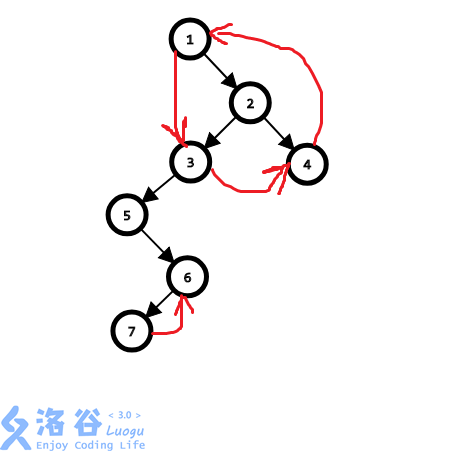
(2->3换成1->3其实也行)

红边为被跳过的边
图中仅靠黑色的边是无法构成强连通分量的 必须加上红色边才可能能够产生强连通分量

观察到对强连通分量的产生有影响的红色边(1->3无影响)都是从后遍历到的边指向在它之前被遍历到的边的(6<-7)(1<-4)(4<-3)

我们根据每一个点被遍历的顺序给每一个点一个时间戳 代表这个点是第几个被遍历的 称为 \(dfn[i]\)

接下来我们再对每一个点记录这个点的所有出边到达的点的最小时间戳 称为 \(low[i]\)

在遍历出边的过程中 如果这个点能到达比它时间戳小的点 这个点一定可以和某个或某些时间戳比它小的点形成强连通分量

在遍历完所有出边后 如果这个点能到达的时间戳最小的点是它自己 那么这个点不可能和时间戳比它小的点形成强连分量了 那么就把它和它子树中(一个点子树中的点一定比该点时间戳大)所有能够到达它的点放入一个强连通分量

1.关于如何实现 其实只要每遇到一个点就放入栈中
栈中的点时间戳时严格递增的 弹出节点从时间戳大的点往小出栈

2.在回溯时(即遍历完所有出边时)遇到\(low_u=dfn_u\)的点u时直接把在u后入栈的点以及u全部出栈 作为一个强连通分量即可 此时所有无法到达u的节点在这之前已经出栈了

3.在遍历点u出边的过程中 如果该出边对应的点v没有被访问过(dfn为0) 就遍历这个点v 然后将u的low值与v的low值取min 因为v遍历得到的点u一定能遍历到

4.如果该边还在栈中(不属于任何一个连通分量)但是已经被遍历过了 就直接更新low值 道理同上

注意不同的dfs遍历顺序会使得每个点的\(low\)和\(dfn\)造成影响 但是该\(low<dfn\)的点\(dfn\)一定还是小于\(low\)的 该\(dfn=low\)的点也还是相等 对\(low\)和\(dfn\)的相对大小是没有影响的

3.代码实现

\(scc[i]\)带表点\(i\)属于第几个强连通分量

void tarjan(LL u){
	low[u] = dfn[u] = ++ num;
	stk[++ top] = u; // (1)
	for(register int i = hed[u];i;i = nxt[i]){
		register LL v = to[i];
		if(!dfn[v]){
			tarjan(v);
			low[u] = min(low[u],low[v]);
            // (3)
		}
		else if(!scc[v]){
			low[u] = min(low[u],low[v]);
            // 注意这一句 在这里写成low[v]和dfn[v]都是对的
            // 两种写法对强连通分量分解的结果没有影响
            // 但是在割点时必须写作dfn[v]
            //(4)
		}
	}
	if(low[u] == dfn[u]){
		scc[u] = ++ cnt;
		while(stk[top] != u){
			scc[stk[top]] = cnt;
			top --;
		}
		top --; // u出栈
	}
    //(2)
}