Manacher

Manacher

传送锚点

算法功能

在 \(O(n)\) 的时间内求出以每个位置为回文中心的回文子串的长度

算法流程

• 预处理: 在每两个字符中间添加 # 字符, 将偶回文转化为奇回文
• 令 p[i] 表示, 在新的字符串中, 以 \(i\) 为回文中心的最长回文子串的半径
• 所求答案即为: p[i]-1
• 那么, 如何在 \(O(n)\)​ 的时间内求出所有的 p[i] 呢?
• 回文性质的利用:
• 
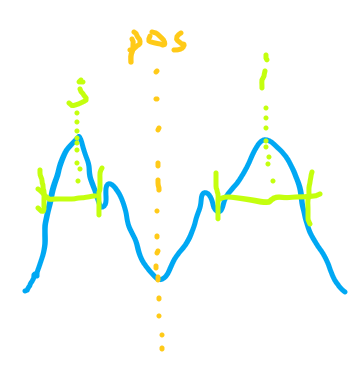
• 我们以对称类比回文
• \(pos\) 是我们找到的右侧最靠右的回文子串的回文中心, 通过 \(i\)​ 处求得的 p[i] 我们可以求得 p[j] ( \(i\) 和 \(j\) 可能画反了不过这不重要), 当然, 在 \(pos\) 串的边界的情况也需要我们考虑

代码

/*************************************************************************
    > File Name: p3805.cpp
    > Author: Typedef 
    > Mail: 1815979752@qq.com 
    > Created Time: 2021年07月23日 星期五 14时47分16秒
    > Tags: 
 ************************************************************************/
#include<bits/stdc++.h>
using namespace std;
const int N=5e7+7;
int n,res=1;
int p[N];
char tmp[N],s[N<<1];
int main(){
	char c=getchar();
	while(c<'a'||c>'z') c=getchar();
	while(c>='a'&&c<='z') tmp[n++]=c,c=getchar();
	s[0]='#',s[1]='#';
	for(int i=1;i<=n;i++)
		s[i<<1]=tmp[i-1],s[i<<1|1]='#';
	n<<=1,n+=2;
	s[n]=0;
	int r=0,pos;
	for(int i=1;i<n;i++){
		if(i<r) p[i]=min(p[(pos<<1)-i],p[pos]+pos-i);
		else p[i]=1;
		while(s[i+p[i]]==s[i-p[i]]) p[i]++;
		if(p[i]+i>r){
			r=p[i]+1;
			pos=i;
		}
	}
	for(int i=0;i<n;i++) res=max(res,p[i]);
	printf("%d\n",res-1);
	return 0;
}