P5785 [SDOI2012]任务安排
代码还是有些问题…
/*
数组没开够,爆零两行泪
ll开成 int,爆零两行泪
多组忘清空,爆零两行泪
dp 没初值,爆零两行泪
深搜没边界,爆零两行泪
广搜忘出队,爆零两行泪
输入没加 &,爆零两行泪
模数没看见,爆零两行泪
-1 不输出,爆零两行泪
越界不特判,爆零两行泪
空间开一倍,爆零两行泪
无向变有向,爆零两行泪
题意没审清,爆零两行泪
文件名起错,爆零两行泪
调试忘删除,爆零两行泪
文件不保存,爆零两行泪
文件不读入,爆零两行泪
文件不输出,爆零两行泪
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=3e5+13;
int n,s;
ll c[N],t[N];//sumc,sumt
ll f[N];
int q[N];
int main(){
cin>>n>>s;
for(int i=1;i<=n;i++){
cin>>t[i]>>c[i];
t[i]+=t[i-1];
c[i]+=c[i-1];//处理前缀和
}
int hh=0,tt=0;
q[0]=0;//f(0)点
for(int i=1;i<=n;i++){
int l=hh,r=tt;
while(l<r){
int mid=(l+r)>>1;
if(f[q[mid+1]-f[q[mid]]]>=(t[i]+s)*(c[q[mid+1]]-c[q[mid]])) r=mid;
else l=mid+1;
}
int j=q[r];
f[i]=f[j]-(t[i]+s)*c[j]+t[i]*c[i]+s*c[n];//见式,不解释
//删去此前的线(点),维护凸包性质
while(hh<tt&&(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]])>=(f[i]-f[q[tt]])*(c[q[tt]-c[q[tt-1]]])) tt--;
//上面这是处理一下斜率,防止精度挂掉
q[++tt]=i;
}
cout<<f[n]<<endl;
return 0;
}
/* 考虑dp
* 状态设计: f[i]
* 集合:将前i个任务处理完的方案数
* 属性:费用最小值
* 状态计算: f[i]
* 不同点:最后一组(当前)的划分情况
* 分类: j∈{0,1,2,...,i-1} 前j一个任务已经划分为一组
* 不变的部分:前k组的最小花费(不包括当前组)
* 求变化的部分:sumt[j]*(sumc[i]-sucm[j])+S*(sumc[N]-sumc[j])
* 做当前任务的费用 机器冷却的费用
* sumt:t的前缀和
* sumc:c的前缀和
* f[i]=min{f[j]+sumt[i]*(sumc[i]-sumc[j])+S*(sumc[N]-sumc[j]}
* 复杂度O(n^2)
*
* 考虑优化,我们需要找到j,使得f[j]
* f[i]=f[j]-(sumt[i]+s)*sumc[j]+sumt[i]*sumc[i]+s*sumc[n];
* y x
* f[j]=(sumt[i]+s)*sumc[j]+f[i]-sumt[i]*sumc[i]-s*sumc[n];
* y = k x + b
* y 斜率 截距
* k为正整数 ,且固定 f(i)不固定
* 所以f(j)必过 1,3象限
* j∈{0,1,2,...,i-1} =>(f[0],sumc[0]),(f[1],sumc[1])...
* 目标:f[i]最小
* 分析:
* 随便取一点(x0,y0)
* 我们可以平移直线,直到经过(x0,y0),然后求得截距,并求得f(i)
* 由于f(i)为正,截距符号为负,则可知截距越大,f(i)越大
* 为是f(i)最小,我们需要使截距尽可能大(数值),低(实际值,位置)
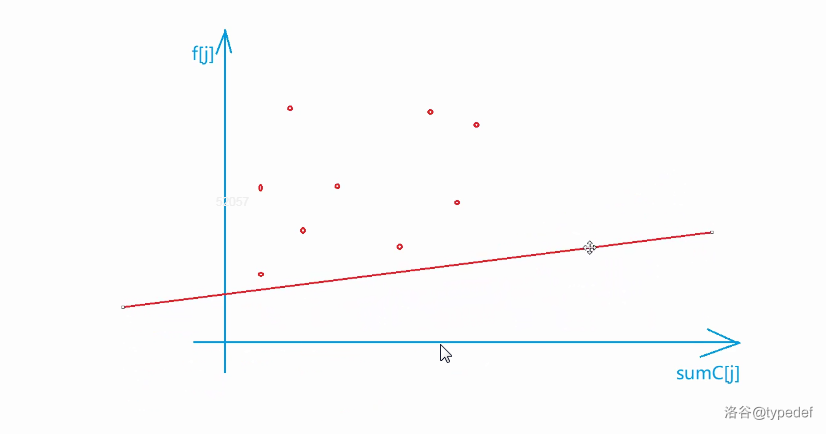
* 由此观之,对于每个i,先求的斜率,再向上平移,直到遇到第一个接触到的点(截距最低)
* (图一)
* 但并不是每个点都会被碰到(产生贡献)
* 因此需要排除不论斜率是多少,都不会被碰到(产生贡献的)
* 怎么排除?任选两个点连线,可以删去该线上方的点(凸包)
* 因此我们只需维护凸包的下边界(核心思想)
* 但在这种情况下,最坏情况还是会T
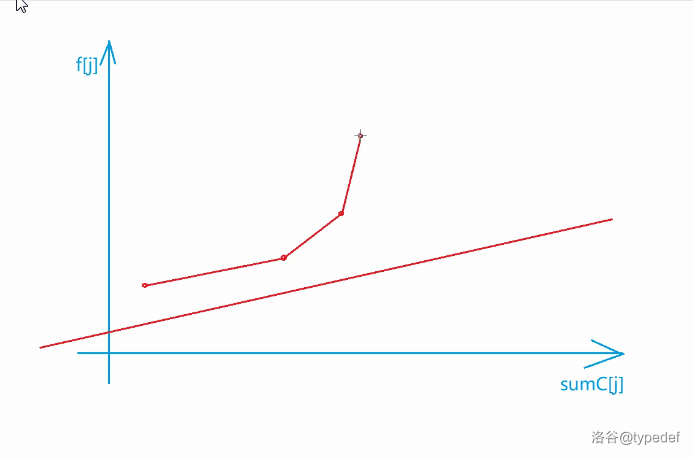
* 不过我们可以看到,直线斜率介于k1,k2之间
* 所以我们需要找到第一个斜率大于k的点
* (图二)
* 在这个凸包下边界中,斜率是单调的,于是可以二分找到我们需要的点 (常规思路)
* 结合本题,两个sum数组也是单调的,这意味着我们从前往后枚举i时,斜率是单调递增的
* 又由于c是大于零的正整数sumc[i]也是递增的,在图像上体现为:下一个点在当前点的右侧(点的横坐标单调递增)
* 所以本题可以不用二分
* 递增的斜率...(很重要一个条件)
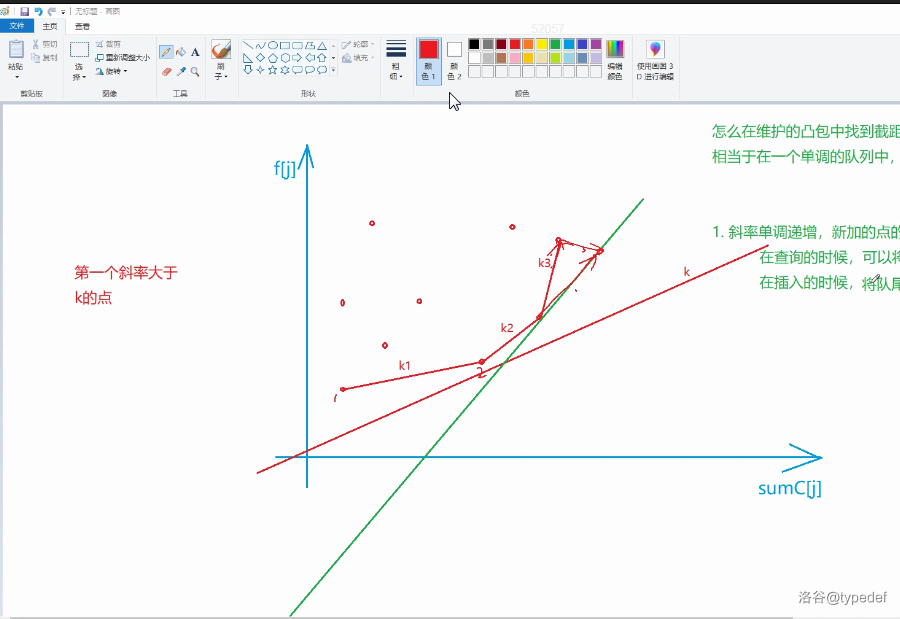
* 在枚举某根线时,这根线的斜率若比凸包的某一根线的斜率大
* 那么可以删掉这根线下面的点(下面的线斜率都比这根小,因此以后一定不会被用到,因为后面的线的斜率更大)
* 在查询时,可以把上述(对头小于当前斜率)的点从队头删掉
* 在插入的时候,有横坐标单调的性质可知,该点一定不会被删掉,所以我们只需更新其他的点(将队尾所有不在凸包上的点全部删掉)
* 每个点只会出队入队一次,复杂度O(n)
* (图三)
* 实现细节:
* (f(2)-f(1))/(sumc(2)-sumc(1))<=sumt(i)+s(队头判断斜率更小的点)
* (f(tt)-f(tt-1))/(sumc(tt)-sumc(tt-1))>=(f(i)-f(tt))/(sumc(i)-sumc(tt))(插入时维护凸包删边性质)
* q[tt]表示凸包最右上的点的编号
* q[hh]表示凸包最左下点的编号
* (啊我累死了)
*/