传递闭包

概念

“传递闭包、即在数学中，在集合X上的二元关系R的传递闭包是包含R的X上的最小的传递关系。” ——《百度百科》

人话 : 建立传递闭包的过程,就是给定一个有向(无向)图,对于节点 i 和节点 j ,如果他们联通但不直接相连,我们就建一个 i 到 j 的边.

求法

我们可以用 Floyd 算法在 $O(n^3)$ 的时间内求得传递闭包

我们用 d(i,j) 表示原图 , g(i,j) 表示它的传递闭包

g(i,j) 是一个无权图,若从 i 出发,可以到达 j 则为 1 ,否则为 0

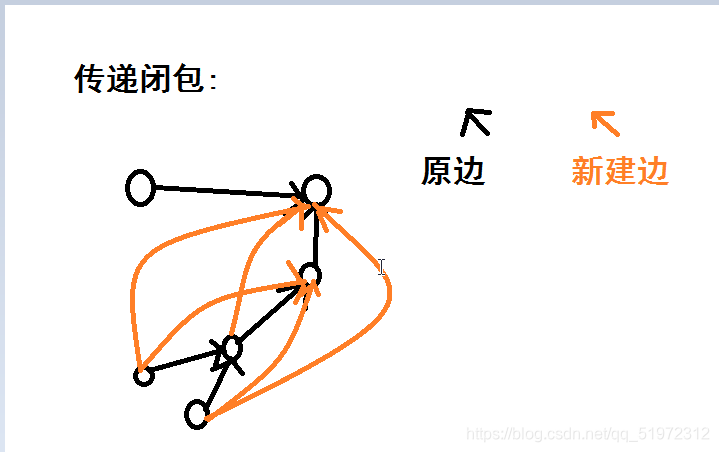
初始化:

g(i,j)=d(i,j)

Floyd:

for(int k=0;k<n;k++)
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			if(g[i][k]&&g[k][j]) 
				g[i][j]=1;

貌似和Floyd没啥区别

完整代码

累了,不想写

应用

运用传递闭包的题目往往会有明显的传递性出现

AcWing343. 排序

思路整理

题目中明示了…不等式的传递性…

如果发现 $A>A$ ,那无疑是矛盾的

例:
$A<B$
$A<C$
$B<C$
$C<D$
$B<D$
$A<B$

我们只需前四个条件就可以退出 $A,B,C,D$ 间的关系

类似的,在计算过程中,我们可以对于当前的条件求传递闭包

如果 d(i,j)=1说明关系已确定( $i<j$ )

判断矛盾 d(i,i)=1

唯一确定: d(i,j)和d(j,i)中有且仅有一个等于一

否则:关系不唯一

循环中若发现矛盾或唯一确定,那么直接退出

否则继续循环,若循环结束后还没确定,那么再输出

那么如何排序呢?(即确定 $A,B,C,D...$的关系)

我们可以每次找到当前未标记的最小的值,然后输出并标记

代码:

/*************************************************************************
    > File Name: 343排序.cpp
    > Author: typedef
    > Mail: 1815979752@qq.com 
    > Created Time: 2020/11/14 21:32:16
 ************************************************************************/
#include<bits/stdc++.h>
using namespace std;
const int N=26;
int n,m;
bool g[N][N],d[N][N];//g是传递闭包,d是
bool st[N];//st数组是输出标记
void floyd(){
	memcpy(d,g,sizeof(d));
	for(int k=0;k<n;k++)
		for(int i=0;i<n;i++)
			for(int j=0;j<n;j++)
				d[i][j]|=d[i][k]&&d[k][j];//传递闭包
	return;
}
int check(){
	for(int i=0;i<n;i++)
		if(d[i][i])
			return 2;//发现矛盾
	for(int i=0;i<n;i++)
		for(int j=0;j<i;j++)//考虑i==j的情况
			if(!d[i][j]&&!d[j][i])
				return 0;//无法确定关系
	return 1;//确定解
}
char get_min(){
	for(int i=0;i<n;i++)
		if(!st[i]){
			bool flag=1;
			for(int j=0;j<n;j++)
				if(!st[j]&&d[j][i]){
					flag=0;
					break;
				}
			if(flag){
				st[i]=1;
				return 'A'+i;
			}
		}

}
int main(){
	while(cin>>n>>m,n||m){
		memset(g,0,sizeof(g));
		int type=0,t;
		for(int i=1;i<=m;i++){
			char str[5];
			cin>>str;
			int a=str[0]-'A',b=str[2]-'A';
			if(!type){
				g[a][b]=1;
				floyd();
				type=check();
				if(type) t=i;
			}
		}
		if(!type) puts("Sorted sequence cannot be determined.");
		else if(type==2) printf("Inconsistency found after %d relations.\n",t);
		else{
			memset(st,0,sizeof(st));
			printf("Sorted sequence determined after %d relations: ",t);
			for(int i=0;i<n;i++) printf("%c",get_min());
			puts(".");
		}
	}
	return 0;
}

理论上说,我们并不用在加边的时候跑一遍$Floyd$

我们只需对新加的边涉及的点进行更新连边

这样做的复杂度是$O(n^2)$

优化后的代码:

/*************************************************************************
    > File Name: 343排序.cpp
    > Author: typedef
    > Mail: 1815979752@qq.com 
    > Created Time: 2020/11/14 21:32:16
 ************************************************************************/
#include<bits/stdc++.h>
using namespace std;
const int N=26;
int n,m;
bool g[N][N],d[N][N];//g是传递闭包,d是
bool st[N];//st数组是输出标记
void floyd(){
	memcpy(d,g,sizeof(d));
	for(int k=0;k<n;k++)
		for(int i=0;i<n;i++)
			for(int j=0;j<n;j++)
				d[i][j]|=d[i][k]&&d[k][j];//传递闭包
	return;
}
int check(){
	for(int i=0;i<n;i++)
		if(d[i][i])
			return 2;//发现矛盾
	for(int i=0;i<n;i++)
		for(int j=0;j<i;j++)//考虑i==j的情况
			if(!d[i][j]&&!d[j][i])
				return 0;//无法确定关系
	return 1;//确定解
}
char get_min(){
	for(int i=0;i<n;i++)
		if(!st[i]){
			bool flag=1;
			for(int j=0;j<n;j++)
				if(!st[j]&&d[j][i]){
					flag=0;
					break;
				}
			if(flag){
				st[i]=1;
				return 'A'+i;
			}
		}

}
int main(){
	while(cin>>n>>m,n||m){
		memset(d,0,sizeof(d));
		int type=0,t;
		for(int i=1;i<=m;i++){
			char str[5];
			cin>>str;
			int a=str[0]-'A',b=str[2]-'A';
			if(!type){
				d[a][b]=1;
				for(int x=0;x<n;x++){
					if(d[x][a]) d[x][b]=1;
					if(d[b][x]) d[a][x]=1;
					for(int y=0;y<n;y++)
						if(d[x][a]&&d[b][y]) d[x][y]=1;
				}	
//				floyd();
				type=check();
				if(type) t=i;
			}
		}
		if(!type) puts("Sorted sequence cannot be determined.");
		else if(type==2) printf("Inconsistency found after %d relations.\n",t);
		else{
			memset(st,0,sizeof(st));
			printf("Sorted sequence determined after %d relations: ",t);
			for(int i=0;i<n;i++) printf("%c",get_min());
			puts(".");
		}
	}
	system("pause");
	return 0;
}