CF1381A3 Prefix Flip(构造,一个不行就多拉一个下水)
前言:之所以会有 A3 是因为算是 A2 的加强版吧。
\(\text{STO}\) \(\color{black}{\text{T}}\color{red}{\text{erryWang}}\) \(\text{ORZ}\)
Description
给定 \(01\) 文本串,母串以及两串的长度 \(n\) ,给定一种操作,可以对文本串任意前缀进行 \(01\) 取反,并同时反转整个选定的前缀。
求一种不多于 \(n + 1\) 次操作的方案,使得文本串转变成母串。
多测。
\(\sum n \leq 3 \cdot 10 ^ 5\)
(原题 A2 的要求是操作次数不超过 \(2n\) )
Analysis
感觉这种操作非常的莫名其妙,又是取反还有翻转,不知道该怎么从操作本质上下手了。
所以会有很多奇奇怪怪的想法,不过我们要直切主题,就暂时不管其他奇奇怪怪的算法了。
我们不用想那么多通过什么技巧能多少多少次还原一个区间,只需要想,假如操作不是前缀,有什么不一样的地方。
相比之下,前缀操作明显的特点就是假如后半部分已经还原,就不再需要照顾,所以我们可以考虑倒序还原。
看操作的本质,我们有什么是可以直接掌控的,能发现对于第一位的前缀,它的翻转是没有体现出来的,从而我们可以直接控制第一位的 \(01\) 。
而要体现出翻转的特性的话,第一位一定会翻到最后一位,所以我们可以通过控制第一位的 \(01\) ,然后把一个前缀翻转,能够至少还原后缀的一位。
所以每次至多两次操作还原一个位置,总体就能很好地控制在 \(2n\) 操作内。
不过数据强度不是很大的话,这个东西是很容易下 \(n + 1\) 的,不过为了严谨性,我们还是认为这个做法只能做原题。
Solution
idea from \(\color{black}{\text{T}}\color{red}{\text{erryWang}}\) from \(\color{red}{\text{icecuber}}\)
其实就是上一个做法的改编版。
我们考虑到对于每一位我们只是有可能要做翻转第一位的 \(01\) ,假如我们必须要只用一次复原一位咋办。
不妨换一种思路,我们改成均摊一位一次,相当于我们通过放宽操作次数,但是同时让多位同时满足。
我们可以理解成我一个人一次性解决不了,我就在拉一个人下水,但是两次能同时解决掉两人。
提前放一句话,因为对 \(b\) 的操作倒过来是等价于对 \(a\) 操作,所以本质上母串可以是两者的任何一个,所以我们仅对文本串是 \(a\) ,母串是 \(b\) 的情况讨论(同时注意我们是对于每一个情况都要让两个串都作为母串做一次判断)。
同时,我们先提前假设我们处理到了第 i 位。
- \(a_i = b_i\)
这种情况非常舒服,因为你发现根本没有翻转什么事,直接删掉就行了。
- \(a_1 \neq b_i\)
否则,我们尝试通过一次操作让母串增加一位相等,有翻转+取反,所以母串的最后一位就对应了文本串的第一位的相反值,所以就会有上面那个条件。
- \(b_{i - 1} = b_i\)
之前的算法到这里就没有然后了,所以我们就只能考虑再拉一位下水。
因为有了之前不满足的条件,首先就有 \(a_1 = b_i\) ,所以也有 \(a_1 = b_{i - 1}\) ,现在因为牵扯到了两位,所以要考虑 \(a_2\) 的值了。
因为 \(a_1\) 的值取反之后就不等于最后一位,所以必须先取反一次:
如果 \(a_1 = a_2\) 的话,就有 \(a_2 = b_{i - 1}\) ,所以 \(a_2\) 也要先取反一次,一合计发现对前两位操作就算翻转也不影响,再对整个串操作就可以了。
否则就更简单了,第二维都不用管了,直接对第一位操作,再对整个串操作就行了。
两次,完美。
- \(a_1 = a_2\)
同样利用上之前不满足的条件: \(a_1 = b_i,\ b_{i - 1} \neq b_i\) 。
所以可以由此推得 \(a_2 \neq b_{i - 1}\) ,整合一下,第二位并不需要翻转,只需要操作第一位,再把整个串操作一次就够了。
两次,完美。
- \(a_{i - 2} \neq a_{i - 1}\)
现在又没有头绪了,只好把眼光放到第三位上,再拉一位下水。
\(a_i \neq b_i,\ a_1 = b_i,\ b_{i - 1} \neq b_i,\ a_1 \neq a_2\) ,当然因为之前的所有操作 \(a\) 和 \(b\) 都做过母串,所以上面的条件 \(a\) 和 \(b\) 互换也是可以的(不然推不动)。
所以整个一串加上 \(01\) 只有两种取值:
所以我们可以先操作 \(i - 1\) 再操作 \(i\) 就可以把 \(a_{i - 2},\ a_{i - 1}\) 右移一位,并且两次操作不影响数值,于是就匹配上两位了。
两次,完美(虽然实际上用了三位,但是只还原了两位)
- 没有什么情况的了
所有条件都不管用怎么办,那么现在两个串应该长这个样子了(嫖一张 \(\color{black}{\text{T}}\color{red}{\text{erryWang}}\) 的图):
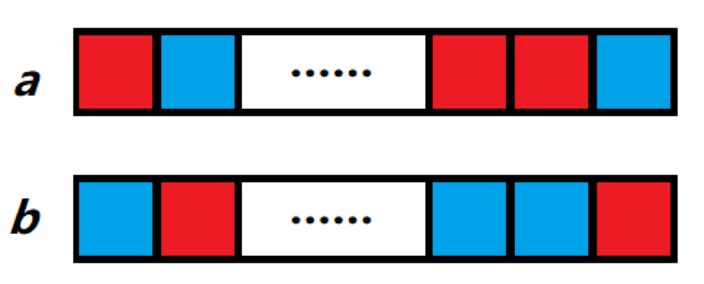
(其中不同的颜色就表示不同的数值)
现在是不得不拖第三位下水了,这也就意味着我们可以操作三次了。
首先我们可以向上一个操作把 \(a_{i - 2},\ a_{i - 1}\) 右移一位,欸,最后一位就满足了。
同时我们也清楚 \(a_1,\ a_2\) 也都会右移一位,而此时第一位上是取反了的 \(a_i\) ,对着上面那张图看, \(a\) 前两位就都是红色了。
假如我们再对 \(i - 1\) 操作,对应到 \(b_{i - 1},\ b_{i - 2}\) 恰好都是蓝色,正好是我们想要的。
所以剩下的这种情况我们可以通过操作 \(i - 1,\ i,\ i - 1\) 来还原三位,非常舒服。
但是这没完,我们发现最后一种操作的上限至少是 \(i >= 5\) ,所以最后我们可能会剩下 \(i = 1,\ 2,\ 3,\ 4\) 的位数没有还原。
怎么办呢, Analysis 的做法会让我们不能保持上限 \(n + 1\) 的。
不过考虑到位数过少,我们可以尝试暴力枚举然后尝试每一种翻转可能,确定一个不超限制的方案。
但是有例外,样例中有这么一个东西:
2
01
10
3 1 2 1
我们发现这个例子必须要用到 \(3\) 次操作,算是一个唯一的例外( \(a\) 和 \(b\) 反过来当我没说),所以即使我们从大局上看上限是 \(n\) 的,但是因为这个例外,我们也只能做到 \(n + 1\) 的了。
Code_Ana
Code_Ana
/*
*/
#include
using namespace std;
#define File(a) freopen(a".in", "r", stdin), freopen(a".out", "w", stdout);
#define Check(a) freopen(a".in", "r", stdin), freopen(a".ans", "w", stdout);
typedef long long ll;
typedef unsigned long long ull;
typedef __int128 i7;
typedef std::pair pii;
#define fi first
#define se second
#define mp std::make_pair
#define eps 1e-6
const int mod = 1e9 + 7;
template
inline int M(A x) {return x;}
template
inline int M(A x, B ... args) {return 1ll * x * M(args...) % mod;}
#define mi(x) (x >= mod) && (x -= mod)
#define ad(x) (x < 0) && (x += mod)
const int N = 3e5 + 10;
int n, a[N], b[N];
char s[N], t[N];
inline void mian() {
std::cin >> n >> s >> t;
for (int i = 1; i <= n; ++i) {
a[i] = s[i - 1] - '0';
b[i] = t[i - 1] - '0';
}
int l = 1, r = n, fg = 0;
std::vector an;
for (int i = n; i >= 1; --i) {
a[r] ^ fg ^ b[i] && (
!(a[l] ^ fg ^ b[i]) && (an.emplace_back(1), a[l] ^= 1),
an.emplace_back(i), std::swap(l, r), fg ^= 1
);
l < r && (--r); l > r && (++r);
}
std::cout << an.size() << " ";
for (int v : an) std::cout << v << " ";
std::cout << "\n";
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
// File("flip");
int t; std::cin >> t; while (t--) mian();
return 0;
}
Code_Sol
Code_Sol
/*
*/
#include
using namespace std;
#define File(a) freopen(a".in", "r", stdin), freopen(a".out", "w", stdout);
#define Check(a) freopen(a".in", "r", stdin), freopen(a".ans", "w", stdout);
typedef long long ll;
typedef unsigned long long ull;
typedef __int128 i7;
typedef std::pair pii;
#define fi first
#define se second
#define mp std::make_pair
#define eps 1e-6
const int mod = 1e9 + 7;
template
inline int M(A x) {return x;}
template
inline int M(A x, B ... args) {return 1ll * x * M(args...) % mod;}
#define mi(x) (x >= mod) && (x -= mod)
#define ad(x) (x < 0) && (x += mod)
struct Flipper {
std::deque p;
int siz;
std::vector all;
bool fli;
Flipper(string ni) {siz = fli = 0; for (auto c : ni) p.push_back(c - '0'), ++siz;}
inline void pop() {--siz; fli && (p.pop_front(), 1); !fli && (p.pop_back(), 1);}
int operator [](int i) {
i < 0 && (i += siz);
if (fli) return p[siz - 1 - i] ^ 1;
return p[i];
}
inline void flip(int r) {
all.push_back(r > 0 ? r : siz + r);
if (r > 0) {
int l = 0;
fli && (l = siz - r, r = siz);
reverse(p.begin() + l, p.begin() + r);
for (int i = l; i < r; ++i) p[i] ^= 1;
}
else if (!r) fli ^= 1;
else {
int dan;
fli && (dan = p.front(), p.pop_front(), p.push_back(dan ^ 1), 1);
!fli && (dan = p.back(), p.pop_back(), p.push_front(dan ^ 1), 1);
fli ^= 1;
}
}
} ;
int n; string S, T;
inline void mian() {
std::cin >> n >> S >> T;
Flipper a(S), b(T);
auto pop = [&](int cn) {while (cn--) a.pop(), b.pop();};
while (a.siz >= 5) {
if (a[-1] == b[-1]) pop(1);
else if (a[-1] == b[-1]) pop(1);
else if (a[0] == a[-1]) a.flip(0), pop(1);
else if (b[0] == b[-1]) b.flip(0), pop(1);
else if (b[-2] == b[-1]) a.flip(a[0] ^ a[1] ? 1 : 2), a.flip(0), pop(2);
else if (a[-2] == a[-1]) b.flip(b[0] ^ b[1] ? 1 : 2), b.flip(0), pop(2);
else if (a[0] == a[1]) a.flip(1), a.flip(0), pop(2);
else if (b[0] == b[1]) b.flip(1), b.flip(0), pop(2);
else if (a[-3] != a[-2]) a.flip(-1), a.flip(0), pop(2);
else if (b[-3] != b[-2]) b.flip(-1), b.flip(0), pop(2);
else a.flip(-1), a.flip(0), a.flip(-1), pop(3);
}
for (int I = 0; ; ++I) {
bool sig = 0;
for (int S = 0; S < 1 << (I << 1); ++S) {
for (int i = 0; i < I; ++i) a.flip(min(S >> (i << 1) & 3, a.siz));
bool fg = 1;
for (int i = 0; i < a.siz; ++i) fg &= (a[i] == b[i]);
if (fg) {sig = 1; break;}
for (int i = I - 1; i >= 0; --i) a.flip(min(S >> (i << 1) & 3, a.siz));
for (int i = 0; i < (I << 1); ++i) a.all.pop_back();
}
if (sig) break;
}
std::vector ans = a.all;
reverse(b.all.begin(), b.all.end());
ans.insert(ans.end(), b.all.begin(), b.all.end());
std::cout << ans.size() << " ";
for (int x : ans) std::cout << x << " ";
std::cout << "\n";
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int T; std::cin >> T; while (T--) mian();
return 0;
}

