打败俺的 ARC141 D
C 是不可能会的,永远都不会的,D 好不容易看懂官方题解,就被 defeat 了。。
拖着我这副老身躯尝试讲懂这个 D 思考的心路历程。。
Description
给定一个长度为 n 的数列 a ,对于每一个位置,求能不能在必选这个数的前提下,选出 m 个数的数列 b ,使得该数列互不为倍数。
\(m \leq 3 \cdot 10 ^ 5,\ m \leq n \leq 2m\)
\(1 < a_1 < a_2 <\ ...\ < a_n \leq 2m\)
Analysis
1
这个 \(n\) 和 \(a_i\) 的上限很有意思,但是我是不可能想出来的。
首先不管这些,我们有一个非常基础的想法,就是让自己连向所有数组中出现过且是自己倍数的数,然后尝试在这个纷繁错杂的 DAG 上跑出答案。
可能最多数量可以算,但是我们需要的是规定一个数必选,这样的话存在自己的倍数不能选和对应的倍数空出来的可选的因数,麻烦。
所以但从这个想法上是行不通的。
2
可以考虑考虑计算一个范围使得范围内的数都可以。
看起来就非常不可做,而且怎么看这个区间都不是连续的。
但是直接求解肯定是行不通了,必须要把答案给预处理出来。
3
是不是可以把单个因子数量作为区间考虑项目,这样一定就是一个连续的区间,太少会有可能成为大数的因子,太多会有可能变成小数的倍数,中间不可能会有特殊情况。
可以可以,继续想想。
4
┗|`O′|┛ 嗷, \(2m\) ,那是不是可以单独不考虑因子 \(2\) ,然后对于剩下来 \(m\) 种数(就是奇数拉)去计算一个区间使得 \(2\) 的因子在这个区间内即合法的数量??
好像可以,但是怎么保证在这个范围内选到的数就一定允许能有 \(m\) 个数被选进来??
Proof
可能有点感性(
假如说对于一个奇数,数组内存在两个数是他的倍数且此外因子仅有 \(2\) 。
就像这样:
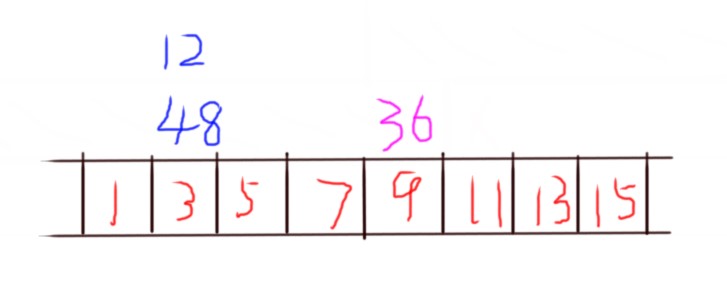
\(12\) 和 \(48\) 就是上面的例子,而 \(36\) 就不在里面。
这样的话 \(12\) 和 \(48\) 是肯定不能全部选到,所以这 \(m\) 个奇数每一个奇数里面的所有数都至多选 \(1\) 个数才是有可能合法的。
举个例子,就比如 \(36\) 选了就一定不能选 \(12\) ,但是可以选 \(48\) ,并且 \(12\) 和 \(48\) 不能同时选(当然有什么 \(96\) 也是可以的捏)。
所以我们只要去用其他数去约束这个范围,假如有数能选到,那就一定能选到,选到的话每个奇数下至多能贡献一个(但是至于是哪个就不仅仅是一种可能了)。
(注意上述约束分“因子约束”和“倍数约束”两种,分别指该数最多在哪里不产生因子,最少在哪里不产生倍数(当然你要反着来也可以,但是切记分两种))
总结下来合法的最基本原理就是数列中刨掉所有 \(2\) 的因子之后所有奇数必须出现,否则肯定选不到 \(m\) 个就暴毙了。
然后如果在所有数的约束下都存在一个数能在它对应的奇数下能被取到,那这个数就一定是合法的了,恰巧只有 \(m\) 个奇数,能选进来也就只有 \(m\) 个。
这也就非常巧妙的解释了 \(n\) 和 \(a_i\) 的上限如此奇葩。
完了吗,真的结束了吗??
其实还有一个问题,还是给个例子:
我们以“倍数约束”为例,因子带 \(3\) 的数为目标,现在有一个因子带 \(9\) 的数和一个因子带 \(27\) 的数。(真实表达都懂,不费键盘了。。)
如果 \(3\) 在 \(9\) 和 \(27\) 的约束下都成立,但是 \(9\) 在 \(27\) 的约束下不成立怎么办,那就倒序计算,用 \(9\) 的答案去更新 \(3\) 的下限。
为什么这样,因为 \(3\) 被 \(9\) 包含了,\(9\) 被 \(27\) 包含了,所以 \(3\) 从某种程度上说是“属于” \(9\) 的,由此, \(9\) 不能做的, \(3\) 就算合法也一定不能选(至于 \(3\) 里面的数合不合法影响不到 \(9\) 里面的)。
倒过来考虑“因子约束”是一个道理的,正推就行。
再有什么问题那都不是问题了/hanx
Solution
目标其实就非常明确了,求每个奇数的适配区间。
其实 Analysis 已经写得差不多了,接下来就仅是一些完善。
我们讲用其他所有数去约束一个奇数的范围并不严谨,因为对于一个奇数下的所有数,我们仅需要一个规定最松的数去约束就行了。反正每个奇数下只能选一个数,能选就选,坦坦蛋蛋荡荡,所以只要最松的满足了就可以。
然后要在加一个从奇数自己的倍数(因子)那里更新。
时间复杂度,枚举奇数 \(O(m)\) ,枚举奇数下的奇数的倍数(就是只乘 \(2\) 的那种) \(O(\log_2 2m)\) ,枚举奇数的倍数均摊 \(O(\ln m)\) 。判断 \(a_i\) 是否合法就是 \(O(1)\) 的。
总时间就是 \(O(n + m\log m)\) ,官方题解说可以把 \(O(\log m)\) 变成 \(O(\log\log m)\) ,我显然是不会的。
可能前后说的不是很清楚,详情见代码。。
Code
Code
/*
*/
#include
using namespace std;
typedef long long ll;
const int N = 6e5 + 10, INF = 1e9;
int n, m, a[N], l[N], r[N];
bool vis[N];
struct ios {
inline char gc() {
static const int IN_LEN = 1 << 18 | 1;
static char buf[IN_LEN], *s, *t;
return (s == t) && (t = (s = buf) + fread(buf, 1, IN_LEN, stdin)), s == t ? -1 : *s++;
}
template inline ios & operator >> (_Tp & x) {
static char ch, sig; ch = gc(); sig = 0;
for (; !isdigit(ch); ch = gc()) {if (ch == -1) return *this; sig |= (ch =='-');}
for (x = 0; isdigit(ch); ch = gc()) x = (x << 3) + (x << 1) + (ch ^ 48);
sig && (x = -x); return *this;
}
} io;
inline double dead() {
char ch = io.gc();
ll s = 0, w = 1, k = 0;
double m = 1; bool is = 0;
while (!isdigit(ch)) {if (ch == '-') w = -1; ch = io.gc();}
while (isdigit(ch) || ch == '.') {
if (ch == '.') is = 1;
else if (!is) s = (s << 3) + (s << 1) + (ch ^ 48);
else k = (k << 3) + (k << 1) + (ch ^ 48), m *= 0.1;
ch = io.gc();
}
return (m * k + s) * w;
}
inline string sead() {
char ch = io.gc();
string s;
while (ch == ' ' || ch == '\n' || ch == '\t') ch = io.gc();
while (ch != ' ' && ch != '\n' && ch != '\t') s += ch, ch = io.gc();
return s;
}
int main() {
io >> n >> m;
for (int i = 1; i <= n; ++i) io >> a[i], vis[a[i]] = 1;
for (int i = 1; i < (m << 1); i += 2) r[i] = INF;
for (int i = 1; i < (m << 1); i += 2) {
int t = -1, c = 0;
for (int k = i; k <= (m << 1); k <<= 1, ++c) if (vis[k] && c <= r[i]) t = c;
r[i] = t;
for (int j = i * 3; j < (m << 1); j += (i << 1)) r[j] = min(r[j], r[i] - 1);
}
for (int i = (m << 1) - 1; i >= 1; i -= 2) {
int t = INF, c = 0;
for (int j = i * 3; j < (m << 1); j += (i << 1)) l[i] = max(l[i], l[j] + 1);
for (int k = i; k <= (m << 1); k <<= 1, ++c) if (vis[k] && c >= l[i]) {t = c; break;}
l[i] = t;
}
for (int i = 1; i < (m << 1); i += 2) {
if (l[i] > r[i]) {
for (int j = 1; j <= n; ++j) puts("No");
return 0;
}
}
for (int i = 1; i <= n; ++i) {
int t = a[i], c = 0;
for (; !(t & 1); t >>= 1) ++c;
if (l[t] <= c && c <= r[t]) puts("Yes");
else puts("No");
}
return 0;
}

