后缀自动机(SAM)囫囵乱讲
(注:本篇博客虽然很详细,但是讲的非常垃圾,而且废话还一大片,所以仅供参考,如果我讲不懂的话把谭老师讲的 \({\rm SA}\) 搞懂就行了,我们相信谭老师讲的一定非常好!
后缀自动机(\({\rm SAM}\))
前置约定
字符串从 \(0\) 开始计数。字符串或集合 s 的符号 \(|s|\) 表示 \(s\) 的大小。
定义
一个字符串 \(s\) 的 \({\rm SAM}\) 是一个能接受 \(s\) 的所有后缀的最小的 \({\rm DFA}\)(确定性有限自动机或确定性有限状态自动机)。
不需要知道什么是 \({\rm DFA}\) ,你只需要知道:
-
\({\rm SAM}\) 是一个 \({\rm DAG}\) ,其中每个节点是一个状态,状态内是一个字符子串,边是状态间的转移,转移都是一个字符,注意每个状态所有出边没有重复。
-
整张图存在一个源点 \(\tau\) ,称为初始状态,其他所有状态都能经由初始状态到达。
-
存在一个或多个终止状态,如果从初始状态出发,到一个终止状态为止,路径上所有转移连接起来是原字符串 \(s\) 的一个后缀,可能会有多条路径,但是同样适用。
-
在所有满足上述条件中,\({\rm SAM}\) 是节点数最少的(这个可以选择性看不到)
性质夹概念带证明
概念-结束位置 \(endpos\)
考虑一个 \(s\) 的一个非空字串 \(t\) ,我们计 \(endpos(t)\) 表示字符串 \(t\) 在 \(s\) 中出现的所有结束位置。
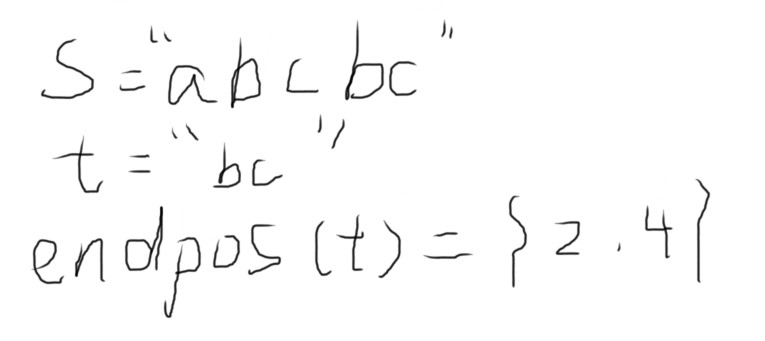
概念-等价类
因为两个非空字串 \(t_1\) 和 \(t_2\) 有可能存在 \(endpos\) 相等的情况,对于每种不同的 \(endpos\) 称所有 \(endpos\) 相等的字串组成的集合为若干个等价类。
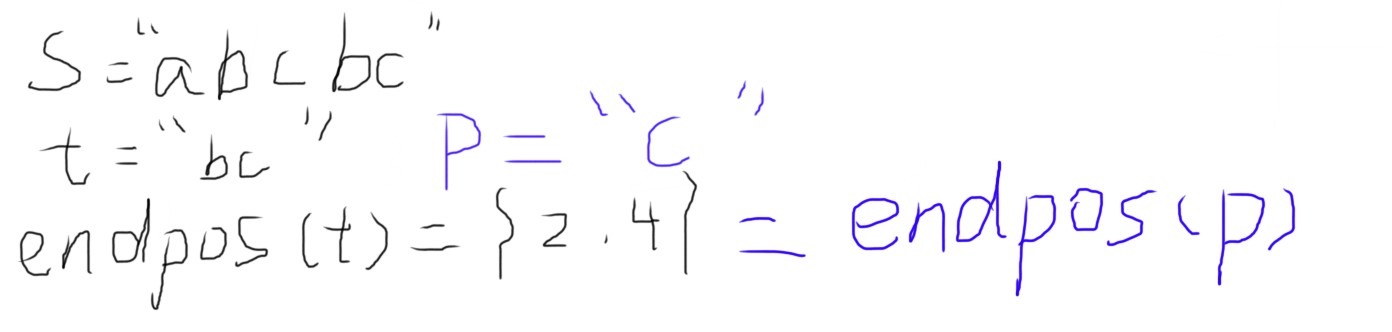
引理 1
如果两个非空子串 \(t_1\) 和 \(t_2\) 的 \(endpos\) 完全相等,且规定前者大小更小,那么前者是后者的后缀,且只在后者中出现一次。
分析:如果要求 \(endpos\) 完全相同的话,结尾的几个字符一定是相等的,并且必定包含整个 \(t_1\) 。
引理 2
考虑两个非空子串 \(t_1\) 和 \(t_2\) ,且规定前者大小更小,那么当前者是后者的后缀,有: \(endpos(t_1) \supseteq endpos(t_2)\) ,否则,有: \(endpos(t_1) \cap endpos(t_2) = \emptyset\) 。
分析:前半段是在引理 1 的基础上,存在在 \(t_2\) 没有出现的时候 \(t_1\) 出现了;后半段是因为有不相同的地方,所以不能在每个位置都匹配完。
引理 3
考虑一个 \(endpos\) 的等价类,将集合中所有字符串按长度降序排列,其中没有长度相同的字符串,且后面的是前面的后缀,而且其长度的集合覆盖了一段区间的所有整数。
分析:“没有长度相同的字符串”可以配合引理 1 解决,因为只有自己是所有长度相等中唯一一个是自己的后缀的字符串;“长度的集合覆盖了一段区间的所有整数”可以配合引理 2 解决,因为倘若 \(t_1\) 是 \(t_2\) 的后缀,那么对于每一个长度在两者之间的字符串,都能用同样的道理说明是 \(t_2\) 的后缀。
概念-后缀连接 \(link\)
考虑 \({\rm SAM}\) 中一个非 \(\tau\) 的状态 \(v\) ,设 \(u\) 为 \(v\) 对应的 \(endpos\) 中大小最大的那个。
然后考虑 \(u\) 中所有后缀,取长度最长的一个和 \(u\) 不在同一个等价类的字符串 \(w\) ,将 \(v\) 的 \(link\) 连向 \(w\) 。
注意,不可能不存在这样的 \(w\) ,因为还有空集,也就对应了初始状态 \(\tau\) 。

所以状态 \(abb\) 和 \(bb\) 的后缀链接都要连向 \(b\) ,而 \(b\) 就要连向空集 \(\tau\)
性质 4
没啥技术但是是我加的哈哈哈(
对于一个非 \(\tau\) 的状态 \(v\) ,其 \(link\) 对应的等价类中所有字符串都是 \(v\) 中字符串的后缀。
分析:引理 3 + \(link\) 概念
引理 5
所有后缀连接反向之后构成一颗以 \(\tau\) 为根的树。
分析:考虑一个不是 \(\tau\) 的状态 \(v\) ,后缀链接连到的状态因为根本不和自己属于一个等价类,并且长度是严格减小的,所以最后必然会连到 \(\tau\) ,还有由于每个状态只有一个入边(反向后),所以整体上就是一棵树。
概念-parent树
没毛用。。不管他
(我是说概念没毛用,因为他说的就是引理 5 ,但没说 parent树 没用哈。。
性质 6
哈哈又是我加的(
parent树 中任意一个状态 v 的儿子们的 endpos 相互交为空。
分析:如果有交,那么必然会被分进一个状态,并且两个集合肯定有包含关系,详见性质 4 和引理 2 。
一些必要的符号
我们设 \(longest(v)\) 表示一个等价类中最长的那个字符串, \(len(v)\) 为其长度;记 \(shortest(v)\) 为等价类中最短的那个字符串, \(minlen(v)\) 为其长度。
引理 3:这个等价类所有字符串的长度覆盖了区间 \([minlen(v), len(v)]\) 中的每个整数。
后缀连接 \(link\): \(minlen(v) = len(link(v)) + 1\) 。
后缀连接树
这个指的就是那个 parent树 哈。
- 如果 \(u\) 是 \(v\) 的祖先,那么 \(u\) 的等价类中所有字符串都是 \(v\) 的等价类中所有字符串的后缀。
- 分析:性质 4 从父亲到祖先。
- \(s_{1-i}\) 与 \(s_{1-j}\) 的最长公共后缀为 \(longest(lca(i, j))\)
- 分析:根据 \(link\) 的概念,所有状态的父亲内的所有字符串都是后缀,所以 \(lca\) 就满足一定是后缀,因为 \(lca\) 是所有满足条件中的最近祖先,所以 \(lca\) 满足最长,然后取状态里面最长的就行了。
- 一个非 \(\tau\) 的状态 \(v\) 的本质不同子串的个数为 \(len(v) - len(fa)\)
- 分析:引理 3 然后稍微想想,其实整个状态里面本质不同子串就是从 \(shortest\) 到 \(longest\) 长度依次增大的这些子串呀,又因为有 \(minlen(v) = len(fa) + 1\) ,相当于 \(len(v) - len(fa)\) 表示的就是本质不同子串数量。
- 一个非 \(\tau\) 的状态 \(v\) 中每个子串在原串中的出现次数相等,且为以 \(v\) 为根的子树中非 \(clone\) 状态的个数之和(这里要知道 \(clone\) 是什么,具体在后面)
-
分析:前半段没啥问题,那就来看后半段。同时,我们注意到 \(clone\) 只是从一个现有状态里面“抢”了一点在新位置多出现的字符串,但是这个位置实际上对应的是状态 \(cur\) ,所以 \(clone\) 不能算数。
-
因为每次转移之后最靠前出现的位置一定不会再有贡献了。由性质 6 ,我们能知道这些儿子的出现位置交集为空,于是所有结束位置不会出现两次。所以最终每个位置会贡献一个状态,总和也就是出现的总次数。
构造 \({\rm SAM}\)
首先,这是一个在线的算法,即每次逐个添加一个字符并维护当前 \({\rm SAM}\) 。
记 \(las\) 为添加新字符 \(c\) 前整个字符串对应的终止状态,然后创建一个新状态 \(cur\) ,易知有 \(len(cur) = len(las) + 1\) ,然后剩下的任务就是要解决 \(link\) 的问题。
我们从状态 \(las\) 开始往上用 \(link\) 跳,如果没有字符 \(c\) 的转移就添加,直到存在就停下,记为状态 \(p\)
situation1
如果 \(p\) 是 \(-1\) ,那么说明这个字符 \(c\) 是首次出现,将 \(link\) 赋为初始状态 \(0\) ,完成。
situation2
如果存在 \(p\) ,那么通过转移 \(c\) 到一个新状态 \(q\) 。如果有 \(len(q) = len(p) + 1\) ,将 \(link\) 赋为 \(q\) ,完成。
situation3
如果不是,那么我们复制一遍 \(q\) ,创建为新状态 \(clone\) ,把 \(q\) 除了 \(len\) 的所有信息复制到 \(clone\) 上,并将 \(len(clone)\) 赋为 \(len(p) + 1\) 。然后将 \(cur\) 和 \(q\) 的 \(link\) 都指向 \(clone\) 。
最后我们要让 \(p\) 继续往上跳,假如有一个向 \(q\) 的字符 \(c\) 的转移,就重新定向到 \(clone\) ,没有就结束跳。
(补:因为如果有 \(len(q) \neq len(p) + 1\) 的情况,只有可能是大于,因为如果还是小于,加之有排除了相等的情况, \(p\) 和 \(q\) 的关系就不会是 \(p\) 转移到 \(q\) ,而是反过来。)
最后的最后,三种情况完了之后就可以更新 \(las\) 为 \(cur\) 就行了。
给个 \({\rm SAM}\) 的样子,扒个图(OI-wiki 上的):
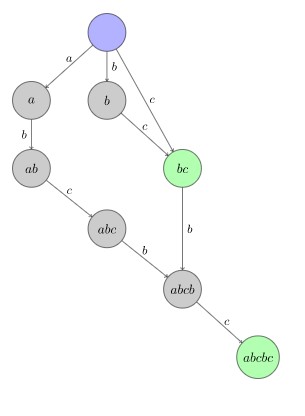
正确性(实际上还是分析)
整个 \({\rm SAM}\) 会大概由两种情况组成,一种是对于转移上的两个状态 \(p,\ q\) ,有 \(len(q) = len(p) + 1\) ,这种我们算连续性的转移,而其他的就叫非连续性转移。
很容易发现这两种转移是完全分离的,前者属于构造中的前两种情况,后者属于第三种情况。
并且前两种情况建立完就不会变了,后者能感觉到是有可能发生变化的,因为 \(p\) 在往上面跳的话, \(len\) 只会变得更小,必然还会满足条件,也就会继续改变一些非连续性转移。
开端
加入新字符 \(c\) ,同时新建一个状态 \(cur\) ,因为前面的半成品 \({\rm SAM}\) 以及已经加入的半个字符串 \(m\) 中,是无论如何找不出一个字符串 \(m + c\) 的,没有问题。
对于 situation1
因为最后是直接跳到了 \(\tau\) ,所以只意味着整个字符串上都没有出现新字符,自然就会有以新字符串开头的子串,连向 \(\tau\) ,没有问题。
对于 situation2
相当于是我们找到了一个字符串 \(k\) 为 \(m\) 的后缀,其中 \(k + c\) 已经在 \(m\) 中出现过了。正好,再加入一个新字符 \(c\) 之后,\(k + c\) 的出现次数是 \(2\) 次,而 \(m + c\) 的出现次数仅为 \(1\) 次,这意味着此时 \(link\) 已经满足了一个条件。
又因为 \(k + c\) 是刚刚出现了 \(2\) 次,由引理 3 可以知道,原先在加入 \(c\) 之前,\(|k| - |m|\) 的长度区间内都有字符串,当 \(k + c\) 和 \(m + c\) 不属于一个等价类后,由于连续性, \(k + c\) 也是当前的等价类中最长的那一个,也就符合了 \(link\) 的另一个条件。
所以最后要把 \(cur\) 的 \(link\) 接上 \(q\) ,没有问题。
对于 situation3
其实我们可以拆成 situation2 和剩余的情况来看,对于前半部分,我们本想和上面一样的处理方法,但是我们发现并没有这样的状态 \(q\) ,所以迫不得已我们只能选择新建一个点 \(clone\) ,然后把原来 \(len(q)\) 中存在的比 \(len(p) + 1\) 长的字符串刨掉,具体体现就是令 \(len(clone) = len(p) + 1\) 。
然后因为更长的部分其实还是属于 \(q\) 这个等价类,但是 \(clone\) 抢走了一部分,所以 \(q\) 的 \(link\) 肯定是要更新的,我们能发现类似 situation2 的情况, \(q\) 能够正好重新怼上 \(clone\) ,所以除了把 \(cur\) 的 \(link\) 接上 \(clone\) ,还要再加上更新 \(q\) 的 \(link\) ,然后把 \(p\) 到 \(q\) 的转移重新定向到 \(clone\)。
这样就够了吗,恐怕还不够吧,因为 \(p\) 前面还有很多状态能跳吧,而根据性质 4, \(p\) 往上跳的状态里面有 \(p\) 中字符串的后缀,同样是有会连到 \(q\) 的可能,同样会由变更,所以同样要修改一遍,重新定向到 \(clone\) 。那这样的话 \(c\) 加入后的影响就处理完了,没有问题!
(PS:下文中 \(n\) 表示字符串长度。)
总状态数(点数)
\([n + 1,\ 2n - 1]\)
初始状态一个,前两个字符都只会有一个新状态,后面每个字符加进来要么新建一个状态,要么新建再新建一个 \(clone\) 。
总转移数(边数)
\([n,\ 3n - 4]\)
首先是连续转移,最少就是整个字符串只有一种字符,转移数只有 \(n\) 个,并且不存在非连续性转移。
假如要上限的话,就是 \(2n - 2\) 个转移数。
(下面都是胡乱口胡的,感性理解一下就行)
考虑非连续性转移的个数,每次对于 situation3 的情况,新建一个状态,意味着检测到一个非连续性转移,但是有可能更新之后没有干掉这条边,同时有可能还会再加一条非连续性转移,最终就有可能会有 \(n - 1\) 条出来。
但是这种情况对应出来的字符串是 \(ab...bb\) ,似乎忽略了前面连续转移,并不满足边数 \(3n - 3\) 的数量,所以我们有了个更紧的上限 \(3n - 4\) ,对应的字符串是 \(abb...bbc\) 。
时间复杂度证明
我们先假设字符集大小为常数,比如 \(26\) 个字母。
放眼整个构造过程,有这么几个时间复杂度的瓶颈:
-
最一开始不断跳 \(las\) 的后缀链接 \(link\) 看是否能添加字符 \(c\) 。
-
situation3 中复制之后继续跳 \(las\) 的 \(link\) ,并重新为 \(clone\) 相关的点重新定向。
我们能明显感觉到的,时间复杂度肯定是跟状态数和转移数有关系,然而这两者都是线性的(前面有准确上下界分析)。
所以这样来看,第一个肯定是线性的,因为每次操作平均只新增 \(1\) 或 \(2\) 个状态,在加入这个字符 \(c\) 之后,之后在加入这个字符的话就会在这个位置停下,所以对于每种字符,均摊下来都是线性的。
第二个瓶颈的话,先这样来想:
我们设 \(linklth(v)\) 表示加入第 \(v\) 个字符后对应状态到初始状态的距离(指跳 \(link\) )。然后看构造的整个过程,发现这样的一个小式子: \(linklth(v) \leq linklth(v - 1) + 1\) 。
然后回到第二个瓶颈,我们再假设往上有 \(k_v\) 个状态需要重新定向,那么 \(linklth\) 又要变小,所以有新式子 \(linklth(v) \leq linklth(v - 1) + 1 - (k_v - 1)\) 。
于是我们对 \(k\) 求个和,发下有这么一个式子:
因为 \(linklen(n)\) 的最大长度为 \(n\) ,所以显然 \(k\) 的总和是线性级别的。
啊,不用担心了。
板子代码
/*
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e6 + 10;
int n, cnt, las, len[N], link[N], ch[N][26];
int tong[N], rk[N]; ll ans;
char s[N];
inline int read() {
char ch = getchar();
int s = 0, w = 1;
while (!isdigit(ch)) {if (ch == '-') w = -1; ch = getchar();}
while (isdigit(ch)) {s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
return s * w;
}
inline void SAM(int c) {
int cur = ++cnt, p = las;
las = cur;
len[cur] = len[p] + 1;
while (p && !ch[p][c]) ch[p][c] = cur, p = link[p];
if (!p) {link[cur] = 1; return ;}
int q = ch[p][c];
if (len[p] + 1 == len[q]) {link[cur] = q; return ;}
int clo = ++cnt;
link[clo] = link[q]; len[clo] = len[p] + 1;
link[q] = link[cur] = clo;
memcpy(ch[clo], ch[q], sizeof(ch[clo]));
while (p && ch[p][c] == q) ch[p][c] = clo, p = link[p];
}
inline void Tong_sort() {
for (int i = 1; i <= cnt; ++i) ++tong[len[i]];
for (int i = 1; i <= cnt; ++i) tong[i] += tong[i - 1];
for (int i = 1; i <= cnt; ++i) rk[tong[len[i]]--] = i;
}
int main() {
cnt = las = 1;
n = read(); scanf("%s", s);
for (int i = 0; i < n; ++i) SAM(s[i] - 'a');
Tong_sort();
for (int i = 1, v; i <= cnt; ++i) {
v = rk[i]; ans += len[v] - len[link[v]];
}
printf("%lld\n", ans);
return 0;
}
应用
1.求本质不同子串个数
给出文本串 \(s\) ,求本质不同子串个数
对 \(s\) 建立 \({\rm SAM}\) ,一种方法见后缀连接树性质 3 ,因为每个状态内没有相同的子串,对所有非 \(\tau\) 的 \(len(v) - len(fa)\) 求和就行。
还有一种就是直接 DP ,因为本质上我们要求的是 \({\rm SAM}\) 的路径条数(定义里面有写),所以在 \({\rm DAG}\) 上跑一遍 DP 也行。
\(d_v\) 表示状态 \(v\) 为根的答案,式子大概是
最终结果就是 \(d_{\tau} - 1\) ,因为还要减去一个空集。
2.求本质不同子串总长度和
给出文本串 \(s\) ,求本质不同子串总长度和
一个意思吧,同样是两种方法,前一种改成什么
“首项加末项乘以项数除以 \(2\) ”就行。
DP 的话除了个数,在另设一个数组 \(g\) 表示总长度,式子就大概是:
意思就是原先 \(u\) 的答案的长度再加上转移中的新字符。
3.求字典序第 \(k\) 大子串
给出文本串 \(s\) ,和多个 \(k_i\) ,求 \(s\) 字典序第 \(k_i\) 大子串
对 \(s\) 建立 \({\rm SAM}\) ,能发现因为转移实际上是 \(26\) 个字母,所以我们可以预处理每个转移下的字串数量(1 的做法),然后找到对应的的转移,依次往下跳就能找到了。
PS:但其实这道题更适合 SA ,OIwiki说的,为什么我不知道,去问谭老师就好啦
4.最小循环移位
给出文本串 \(s\) ,问 \(s\) 在循环移位若干次后的最小字典序
回到字串本身,什么字符串能够包含所有 \(s\) 的循环移位??
\(s + s\) 对吧,那对它做 \({\rm SAM}\) ,贪心的往最小转移上跑,长度跑到 \(|s|\) 就行,并且肯定跑的完,因为如果跑不完那肯定是从后半段开始跑的,那前面还有完全一样的一段,所以不用担心跑不完。
5.检查模式串是否出现
给出文本串 \(s\) ,和多个模式串 \(t\) ,检查这些模式串 \(t\) 是否在 \(s\) 中出现过
对 \(s\) 建立 \({\rm SAM}\) ,因为 \({\rm SAM}\) 存在所有 \(s\) 的子串,所以就把 \(t\) 直接从 \(\tau\) 上跑对应的字符,跑不动就说明不存在,跑完了就说明存在。
6.求模式串出现次数
给出文本串 \(s\) ,和多个模式串 \(t\) ,求这些模式串 \(t\) 在 \(s\) 中出现次数
出现次数无非就是求一个字串 \(endpos\) 集合大小是多少嘛,又因为这些位置对应的每一个非 \(clone\) 状态,而且每个状态内所有字符串是一个等价类,所以出现次数相同,所以我们设 \(f_v\) 表示状态 \(v\) 的出现次数,有式子:
又因为状态之间的转移不会出现状态重复,所以不会存在一个位置是同时在两种状态上转移而来的,所以不会算重什么的。
7.求模式串第一次出现的位置
给出文本串 \(s\) ,和多个模式串 \(t\) ,求这些模式串 \(t\) 在 \(s\) 中第一次出现的位置
直接在构造 \({\rm SAM}\) 时解决,如果不是 \(clone\) 状态,在新建的时候设成 \(len - 1\) 就行了,因为它出现了,否则的话同样复制成对应的状态 \(q\) 的信息,因为 \(clone\) 本质上还是 \(q\) 的一小部分。
但是我们记录的是第一次结束的位置,所以最后搜完 \(t\) 之后剪掉长度就行了。
8.求模式串所有出现的位置
给出文本串 \(s\) ,和多个模式串 \(t\) ,求这些模式串 \(t\) 在 \(s\) 中所有出现的位置
发现其实不需要每个节点都需要记录所有出现次数,因为发现在 parent树 上,一个状态 \(v\) 的儿子们 \(u\) 第一次出现的位置必然 \(v\) 也再次出现了,并且不会重复。
所以我们只需要同上的做法,然后在 \({\rm SAM}\) 上找到模式串对应的状态,继续遍历(注意要刨掉 clone 状态)后代们就得到了所有出现位置。
9.求最短的没有出现的字符串
给出文本串 \(s\) ,求长度最小的没有出现过的字符串
怎么一步到位呢,好像不太行,我们尝试通过一次遍历来确定定位,设 \(f_v\) 表示状态 \(v\) 时答案的长度。注意到要求长度最小,所以答案中第一个不存在的字符一定是唯一并且还在末尾。
如果一个状态的转移存在空缺,标记 \(f_v\) 为 \(1\) ,因为不存在,所以可以作为答案的结尾。否则的话有这样一个式子:
意思就是找所有转移里面不合法长度最短的那一个。最后全部算完之后,倒着推回去,如果有长度相同的随便挑一个就行了。
10.两个字符串最长公共子串
给出两个文本串 \(s\) 和 \(t\) ,求两个文本串的最长公共子串
还是对 \(s\) 建立 \({\rm SAM}\) ,最自然的想法就是对于每一个 \(t\) 的前缀,在 \({\rm SAM}\) 找 \(s\) 的最长后缀,答案显然就是这些所有答案中的最大值。
复杂度接受不了呀,咋办呢??
我们发现其实每次操作的差异仅仅是 \(t\) 的一个字符,所以我们考虑怎么把状态接着上一个继续跑。设两个变量:当前状态 \(v\) 和当前长度 \(lth\) 。
每次加入一个字符 \(c\) 后判断:
-
当前状态是否存在 \(c\) 的转移,如果没有,我们选择让 \(v = link(v)\) ,也就是继续往上找一个状态,同时让 \(lth\) 变更为 \(len(v)\) ,因为想要的是最长的字符串。
-
直到存在转移 \(c\) 或跳到了虚拟状态(即 \(c\) 都没有在 \(s\) 中出现过,这样的话让 \(v = lth = 0\) 就行),让 \(v\) 转移然后让 \(lth++\) 。
11.多个字符串最长公共子串
给出多个文本串 \(s_i\) ,求所有文本串的最长公共子串
受上个做法的启发,我们单独拎一个字符串出来建 \({\rm SAM}\) ,然后把其他字符串往上面跑。
但怎么求公共的??
我们可以每次加入字符处理完之后在对应 \({\rm SAM}\) 上的状态记录一下目前的最大匹配长度。因为要求多个串同时满足,注意要取 \(\min\) ,因为状态内所有字符串互为后缀,所以还是有正确性的。
这样对吗??
样例是这样的: \(abba,\ ab,\ ba\) 。假如我们就用第一个字符串建立 \({\rm SAM}\) ,上个图:
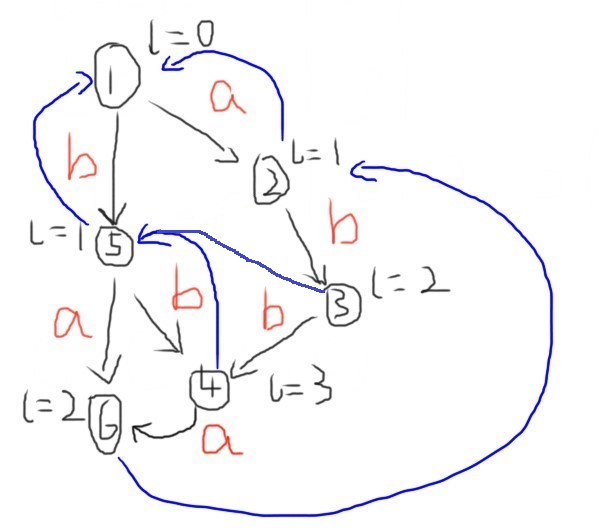
很显然第二个字符串会跑 \(2,\ 3\) ,第三个字符串会跑 \(5,\ 6\) ,但是都只经过了一次,取 \(\min\) 的话,啪唧,全部变回 \(0\) 了,肯定不是答案了。
那错哪里了呢??
我们发现 \(6\) 其实能给 \(2\) 做贡献,因为 \(2\) 中包含的字符串全是 \(6\) 的后缀。所以有这样的改进措施:一个状态能被匹配到的话,他的所有祖先( \(link\) )同样能被匹配到,所以还要从下往上取一遍 \(\max\) 。
莫得问题啦!
12.两个字符串公共子串个数
给出两个文本串 \(s\) 和 \(t\) ,求两个文本串的公共子串个数
受上上一个做法的启发,我们每次新加入一个字符之后找到了一个对应的状态 \(v\) 和长度 \(len\) ,然后我们能发现整个状态内所有长度不大于 \(len\) 的似乎都是子串呀。拿求和不就完了吗??
要去重吧,万一两个地方都能匹配到 \({\rm SAM}\) 上的一个地方呢??
咋去重呢??
在 \(t\) 的 \({\rm SAM}\) 上面跑能做到吧。那咋办呢。我们发现 \(t\) 在 \(s\) 上匹配,和 \(s\) 在 \(t\) 上匹配其实是一个道理吧。所以我们可以反过来设 \(mx_v\) 表示 \(t\) 的 \({\rm SAM}\) 上状态 \(v\) 最长的属于 \(s\) 的子串串长。
那这下又咋算呢??
原先算法在加入字符之后,可能会有几率在 \(s\) 的 \({\rm SAM}\) 上跳 \(link\) 以获取新字符 \(c\) 的转移。这个时候实际上在 \(t\) 上的匹配也会寄掉一点,所以我们尝试在 \(s\) 的 \({\rm SAM}\) 跳完之后,在 \(t\) 的 \({\rm SAM}\) 上再跳,直到两者的状态都合法为止,然后重新更新目前的长度。
所以总的来说,当 \(s\) 的 \({\rm SAM}\) 状态发生变化了, \(t\) 的 \({\rm SAM}\) 就跟着一起变,然后沿路更新 \(mx_v\) 就行了。
这样就对了吗??
受上一个做法的启发,可能会有类似的错误:
(实际上有没有错俺也不清楚,总之是相似的例子,感性理解下就行)
所以更新之后还要全部往祖先上重新取 \(\max\) 。这样的话直接暴力跳链肯定时间复杂度会假,离线下来统一做或许可以。
但是实际上是可以在线的,因为如果一个点的 \(mx\) 已经是 \(len\) ,说明他的所有祖先也会全部这样,就没必要再更新了,所以就可以跳链到 \(mx = len\) 时停止,时间复杂度不会假。
(以下是感性证明,有错的话直接大吼大叫就行:
因为我们要更新是因为 \({\rm SAM}\) 是个 \({\rm DAG}\) ,有多条路径能到达一个状态,造成了一部分点没能更新到答案。所以我们更新就只针对这部分点,停止条件就是到达了一个之前更新过的点。
就像这样:
所以相当于这部分暴力跳链的时间和我们本身在 \(t\) 上转移状态是同级别的,所以是时间真的。
莫得问题啦!!
upd:有更简单的写法:
我们发现其实去重的话全部是建立在 \(t\) 的 \({\rm SAM}\) 已经建立好之后搞的,我们想想能不能在建立的过程中就记录一些必要的信息呢??
能!
我们想要的仅是在第 \(i\) 个字符加进来后 \(endpos\) 第一个元素是 \(i\) 的那些子串。因为 \(link\) 上面所有子串在之前出现过,也必定在 \(i\) 处出现,所以在更靠前的点上已经能记录贡献了,要刨掉这种。
所以在加完第 \(i\) 个字符之后,紧接着记录父亲的最大子串长度,即 \(len(link(cur))\) 的值为数组 \(ha(i)\) ,表示这个状态前要刨掉的长度。正好此时 \(endpos\) 第一个元素为 \(i\) 的子串必然已全部出现,防止后面有 \(clone\) 状态捣乱。
所以我们只需要正常的向求最大公共子串那样求就行了,求完以此把贡献加上 \(lth - ha(i)\)
例题
【模板】最小表示法(应用 4 )
不同子串个数(应用 1 )
[SDOI2016]生成魔咒(应用 1 )
【模板】后缀自动机 (\({\rm SAM}\))(应用 2 )
[TJOI2015]弦论(应用 3 )
SP1811 LCS - Longest Common Substring(应用 10 )
SP1811 LCS - Longest Common Substring II(应用 11 )
[AHOI2013]差异(后缀连接树 性质 2 )sol
[TJOI2019]甲苯先生和大中锋的字符串(萌萌题)sol
扩展
CF914F Substrings in a String(分块)sol
CF1037H Security(线段树合并维护 endpos )sol
[NOI2018] 你的名字(应用 12 + 线段树合并)sol
区间本质不同子串个数(应用 1 + LCT )sol
[CmdOI2019]口头禅(应用 11 + 猫树)sol
[FZOI 4449] 斩尽牛杂(区间本质不同子串个数 Plus)sol
参考资料
(算是个鸣谢把)
-
博文 Суффиксный автомат 的英文翻译版 Suffix Automaton
-
unputdownable 的 \({\rm SAM}\) 学习笔记

