[NOIP2021] 方差
(哈哈,考场想的已经七七八八了但是感觉复杂度不太行就弃了,考后发现基本就是正解的思路了,哈哈)
Analysis
从两个角度出发,一个是公式本身,另一个是操作本身。
Solution
公式本身
先是公式本身,比较自然的,去拆解式子:
因为答案要乘上 \(n ^ 2\) ,所以式子就变成了:
因为众所周知这玩意不受数的实际大小的影响,所以就先钦定数组内最小的数为 \(0\) 。
嗯,好看很多了,主要是算的时候方便了很多,因为这两项是彼此独立的。
操作本身
大概就是可以把一个数变成边上两个数的和减去自己。
画个图,看一下这个操作干了什么:
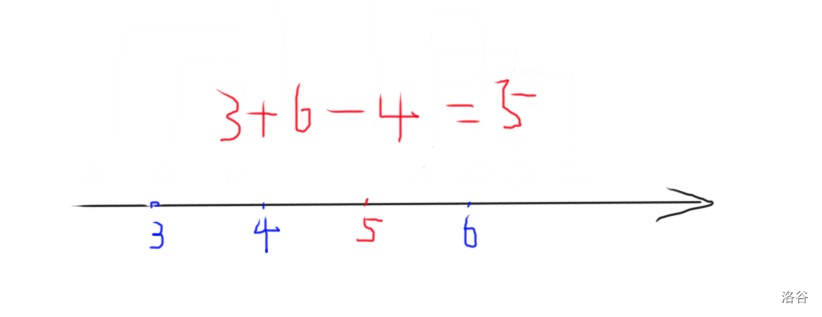
我们学过两个数的平均值是 \(\bar x = (a + b)/2\) ,那么其实很容易理解操作本质上是是让中间的数按边上两个数的平均值对称得到了新数。
所以显然,对同一个数做两次操作就变回原来的数了。
好像还是没什么用。。
那这个对称还有什么好性质吗??
还真有,差分数组 \(d_i\) ,这个不就是所有数的间距,那操作一次不就相当于交换一下相邻的两个间距嘛。
那既然操作次数是若干,那就相当于所有间距的排列顺序可以由我们自己定。
那至此题面上两个我们能挖掘的信息已经搞定了。
手玩一段时间发现没有什么快速的填法,然后注意到数据范围不是很大,考虑直接暴力 DP 。
现在跟答案有关的只有三项:填了多少个间距,目前的 \(a_i\) 总和,目前的 \(a_i\) 总平方和,注意到我们是应该让总和尽可能大,总平方和尽可能小。
由于前两者范围更小一些,那就塞进数组里面:
\(dp_{i, S}\) 表示填了 \(i\) 个间距,数组总和为 \(S\) 的总平方和的最小值。
那么对于一个还未填入的间距,我们可以选择放到最前面或是最后面。
放到最后面的话:
首先总和的话加上了 \(\sum d_j\) ,这样的话才会得到新的 \(a_i\) ,其次总平方和就就是加上了 \(a_i ^ 2\) 。
式子的话就是:
放到最前面的话:
这个比较看起来麻烦,因为后面所有数都因此加上了了一个 \(d_j\) ,总和的话问题不大,只是加了 \(i\) 次 \(d_j\) ,但是总平方和有点麻烦,所以还得稍微推推式子:
所以只要实时记录一下 \(Sum = \sum a_i\) 就可以了。
式子大概就是:
时间复杂度 \(O(n \cdot n \cdot a_i)\) (后面两项就是总和大小)极限在 \(5\cdot 10 ^ 9\) 左右,不太能过。
时间瓶颈在我们枚举的 \(S\) ,考虑还有什么可以优化的。
发现每次数列总和只会有两种加法: \(\sum d_j\) 和 \(i * d_j\) 。那实际上我们只要把 \(d_j\) 从小到大排序,这样保证了 \(\sum d_j < i * d_j\) ,那么每次我们枚举 \(S\) 的上限就只需要加一个 \(i \cdot d_j\) 就行。
虽然这样的话时间本质上还是 \(O(n \cdot n \cdot a_i)\) 的,但是考虑到值域相较于正常题来说小太多了,这导致有大量的间距实际上是 \(0\) ,那么真正有效果的间距最多只有值域大小个。所以时间复杂度来到了 \(O(n \cdot a_i \cdot a_i)\) ,可以通过此题。
刚刚只看了时间问题,但实际上空间也开不下,所以还需要滚动数组。
Code
/*
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e4 + 10, A = 606;
const ll INF = 1e16;
int n, a[N], tmp;
ll var[N], sum, lim;
ll mor, f[2][N * A], ans;
inline int read() {
char ch = getchar();
int s = 0, w = 1;
while (ch < '0' || ch > '9') {if (ch == '-') w = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {s = (s << 3) + (s << 1) + ch - '0'; ch = getchar();}
return s * w;
}
int main() {
// freopen("variance.in", "r", stdin);
// freopen("variance.out", "w", stdout);
n = read();
for (int i = 1; i <= n; ++i) {
a[i] = read();
if (a[i] != 1) var[i - 1] = a[i] - a[i - 1];
}
sort(var + 1, var + n);
for (int j = 0; j <= 600000; ++j) {
f[0][j] = f[1][j] = INF;
}
f[0][0] = 0;
for (int i = 1; i < n; ++i) {
tmp ^= 1;
int now = tmp, pre = tmp ^ 1;
sum += var[i]; lim += i * var[i];
for (ll j = 0; j <= lim; ++j) f[now][j] = INF;
for (ll j = 0; j <= lim; ++j) {
if (j + sum <= lim) f[now][j + sum] = min(f[now][j + sum], f[pre][j] + sum * sum);
mor = (2 * j + i * var[i]) * var[i];
if (j + i * var[i] <= lim) f[now][j + i * var[i]] = min(f[now][j + i * var[i]], f[pre][j] + mor);
}
}
ans = INF;
for (ll j = 0; j <= 600000; ++j) {
ans = min(ans, n * f[tmp][j] - j * j);
}
printf("%lld\n", ans);
return 0;
}

