[IOI2017] Wiring 接线

复盘 pb 讲的题，来写篇题解造福社会。

Description

有 \(n\) 个红色的点，坐标为 \(r_i\) 和 \(m\) 个蓝色的点 \(b_i\) ，问在所有点都至少与一个异色的点连边的情况下，最小花费，其中花费指两点坐标差。

\(n,\ m \leq 10 ^ 5\ ,\ \ r_i,\ b_i \leq 10 ^ 9\)

Analysis

非常烦，因为并不知道到底怎么样才是最小花费。

这种两两配对的这种，其实应该是能想到网络流的，但是因为我水平严重不够，想不出来怎么做，就直接放弃了。。

于是来观察部分分有什么类型，注意到 13 分那个约束条件，就相当于整个数轴上只有两个颜色块。

块，那是不是对于其他情况都可以这么想，那对于任何一个例子，都可以画成这个样子：

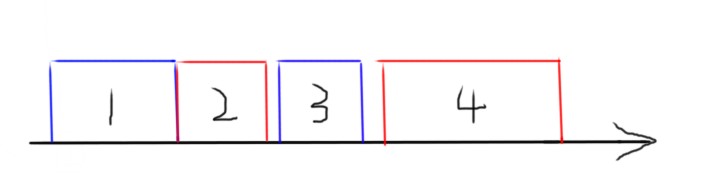
正好每个点连的边的数量没有限制，只是要有边就行，这样子看问题就感觉清晰多了。

Solution

接着 Analysis 中的图，很快应该就能发现，一个颜色块里面的点顶多会跟旁边两个异色块里面的点连边。

因为再往外的话肯定就会先经过一些同色点，让那些点去连更外层的异色点显然会更优。

那么问题逐渐简洁了起来，好极了！！1

那么对于两个颜色块，假设我们已经确定了里面的点要相互连边：

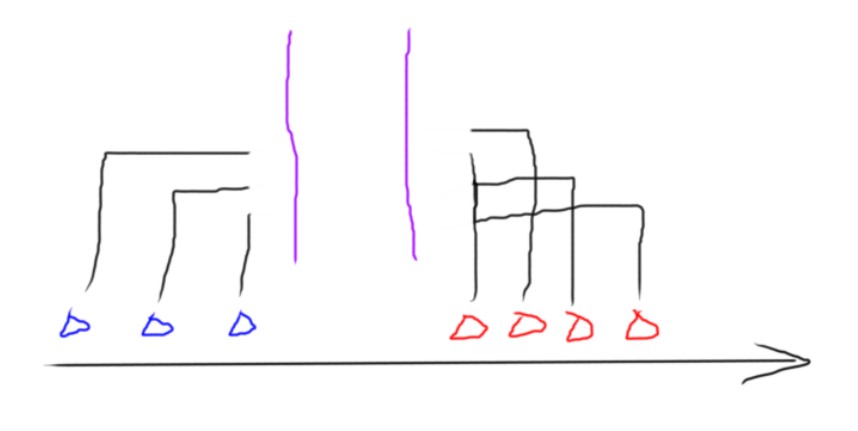
肯定每个点都要伸出去一个边，然后一共会连 \(\max(n,\ m)\) 条，点多的那边就肯定会贪心的把多出来的点连向最靠近自己的异色点，所以对于这个样子的图，花费就是：

\[\sum_{i = 1}^{cnt1}(b_{cnt1} - b_i) + \sum_{i = 1}^{cnt2}(r_i - r_{cnt2}) + \max(n,\ m) \cdot (r_{cnt2} - b_{cnt1}) \]

这玩意能在做前缀和先算好，问题不大。

那些在就相当于我们只要知道在满足条件的情况，一个区间是把多少个点连向前面（剩下的就连向后面）花费最小。

考虑 DP ， \(f_i\) 表示在前 \(i\) 个点的最小花费。

转移的话，我们可以先把所有点划分成若干组前面一段红后面一段蓝的样子。

然后可以直接枚举在哪个地方断开，前半部分向前连边，后半部分向后连边。

然后把前面那一段看从哪里断出来一部分点向后连边更优，这些是可以提前预处理好的（就是套上面的公式），就要注意一下两个区间分出来的两部分的长度关系就可以了。

Code

/*

*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
const ll INF = 1e16;
ll col[N], s[N], cnt, lt[N], rt[N], tot;
ll f[N], pre[N], sum[N], mn[N];

ll min_total_length(std::vector<int> R, std::vector<int> B) {
	ll n = R.size(), r = 0, m = B.size(), b = 0;
	while (r < n && b < m) {
		if (R[r] < B[b]) {
			s[++cnt] = R[r++];
			col[cnt] = 1;
		}
		else {
			s[++cnt] = B[b++];
			col[cnt] = 2;
		}
	}
	while (r < n) s[++cnt] = R[r++], col[cnt] = 1;
	while (b < m) s[++cnt] = B[b++], col[cnt] = 2;
	for (r = 1; r <= cnt; r = b) {
		for (b = r; b <= cnt && col[r] == col[b]; ++b);
		lt[++tot] = r; rt[tot] = b - 1;
	}
	for (int i = lt[1]; i <= rt[1]; ++i) f[i] = INF;
	for (int i = 2; i <= tot; ++i) {
		ll invl = s[lt[i]] - s[rt[i - 1]], S = 0;
		ll lth = rt[i - 1] - lt[i - 1], now = 1;
		for (int j = rt[i - 1]; j >= lt[i - 1] - 1; --j) {
			sum[j] = sum[j + 1] + s[rt[i - 1]] - s[j];
			pre[j] = f[j] + sum[j + 1];
			mn[j] = pre[j] + invl * (rt[i - 1] - j);
		}
		for (int j = rt[i - 1]; j >= lt[i - 1]; --j) pre[j - 1] = min(pre[j - 1], pre[j]);
		for (int j = lt[i - 1]; j <= rt[i - 1]; ++j) mn[j] = min(mn[j], mn[j - 1]);
		for (int j = lt[i]; j <= rt[i]; ++j) {
			S += s[j] - s[lt[i]];
			if (now <= lth) {
				ll lef = rt[i - 1] - now + 1;
				f[j] = S + min(mn[lef - 1], pre[lef] + now * invl);
			}
			else f[j] = S + pre[lt[i - 1] - 1] + now * invl;
			++now;
		}
	}
	return f[cnt];
}