[HNOI/AHOI2018]毒瘤
又是一道虚树好题
Description
给定 \(n\) 个点, \(m\) 条约束关系 \(a\) 和 \(b\) ,表示 \(a\) 和 \(b\) 不能同时被选择。
问有多少种选择方案,答案对 998244353 取模。
题意概括:求一张图上的独立集数量(为了凸显逼格。。)
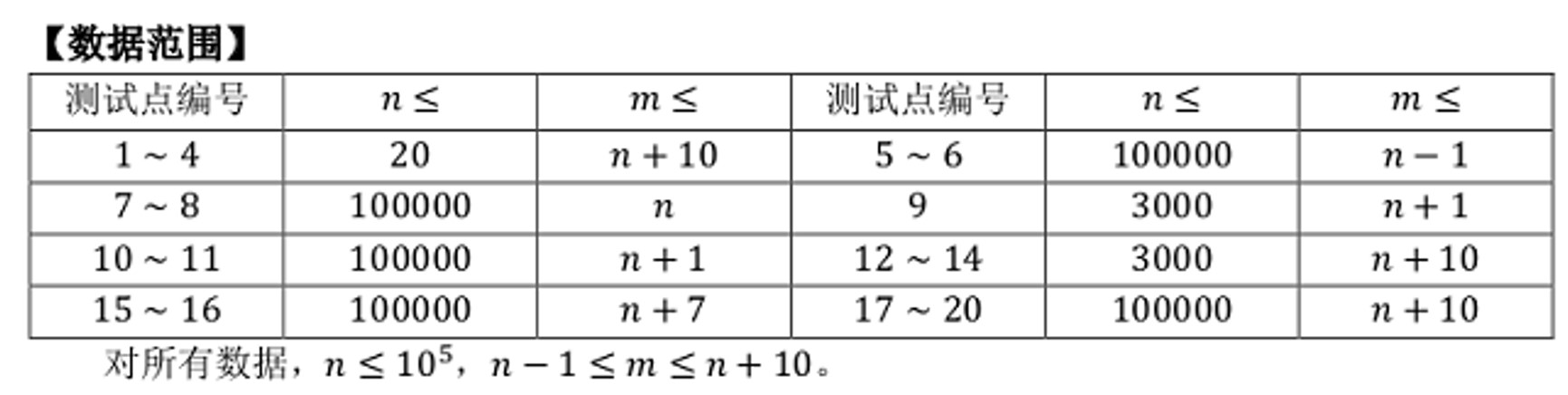
\(n \leq 10 ^ 5\ ,\ n - 1\leq m \leq n + 10\)
Analysis
这个 \(m\) 的范围有点诡异,如果把图建出来,最多只会有 \(11\) 条非树边,或许可以以此作为切入点呢。
一个比较正常的想法,先去想对于一个树的话,怎么做这道题。
这应该是一个基础到家了的树形 DP 吧,\(F_{u, 0/1}\) 表示以 u 为根的子树里面, u 这个节点选 / 不选的方案数,最终答案就是 \(F_{1, 0} + F_{1, 1}\) 。
转移式子就是:
然后就去要去想怎么扩展到一个非树边不超过 \(11\) 个的图上。
Solution
Part1 \(\small O\big(2^{m - (n - 1)} \cdot n\big)\)
由于边很少,我们甚至可以直接枚举,对于每条边 \((u, v)\) (同时钦定 \(u\) 的 dfn 序小于 \(v\) )的状态就是 \((1, 0)\ ,\ (0, 1)\ ,\ (0, 0)\) ( \(1\) 表示选, \(0\) 表示不选),同时注意到后面两种并不排斥,可以一块计算,所以我们就可以以 \(u\) 选 / 不选作为一条边的状态, \(O\Big(2 ^ {m - (n - 1)}\Big)\) 的去枚举,然后 \(O(n)\) 的算。
总体时间复杂度就是 \(O\Big(2^{m - (n - 1)} \cdot n\Big)\) 的啦。
从数据上来看这完完全全能拿到 \(70pts\) 呀!
然后写完过后实测有 \(75pts\) 。。
(到这里的话,个人评价是道蓝以下的 DP 题)
Part2 \(\small O\big(n + 2^{m - (n - 1)} \cdot (m - (n - 1))\big)\)
可以感觉到每次都是进行的相同的操作,只是对于有些点可能确定了选 / 不选,不再存在贡献,就会影响了整个树整体的答案,然后我们就因此重新算了一遍,属实有点亏。
然后想起来非树边一共就 \(11\) 条,考虑把所有多余的边对应的点拎出来建成虚树,那么这样的话最多会有 \(22\) 个关键点,虚树大小也是 \(\leq (44 + 1)\) 。
接下来考虑在虚树上预处理出来一点什么。
想到一开始的那两个式子,很显然不能直接硬算,因为虚树两个有边的点之间可能有不少被省略的点,这样就相当于一条边在原树上可能是一条链。
因为中间的点能被省略掉,说明肯定不是关键点,所以可以正常转移,那么对于原树上一条链 \(u \Rightarrow x_1 \Rightarrow x_2 \Rightarrow ... \Rightarrow x_k \Rightarrow v\) ,假设 \(F_{i, 0 / 1}\) 转移前的值为 \(G_{i, 0 / 1}\) ,转移式子有:
合并带入有:
总的来说,这会转化成一个带系数 \(coe\) 的式子,大概就是:
那么对于虚树上任意两个相连的点,都有类似的式子,可以预处理出这个 \(coe\) ,由于这玩意真的特别像 \(F\) ,同样可以选择大法师处理,也是 \(O(n)\) 。
同样,树上所有点的 \(F\) 也不全都是 \(1\) 了,因为考虑到我们处理的系数什么的都是跟虚树上的点有关,所以只要子树内不包含虚树上的点的话,至始至终答案都是一样的,就把这些点的 \(F\) 按照正常的 DP 做法处理一下就可以了。
统计答案的话,还是先枚举所有非树边的选点的状态,然后按照这个把虚树上的点的初值赋好我们已经预处理好的系数,跑一遍虚树更新答案就行了。
这样按照我们前面设想的系数的含义,相当于是跳过了没有必要再次计算的非虚树点,直接一步到位,然后达到了节省时间的目的。
时间复杂度 \(O\Big(n + 2^{m - (n - 1)} \cdot (m - (n - 1))\Big)\) 。
(由于实现雀食有点麻烦我还是参考了 Soulist 的写法,雀食非常简洁易懂)
Code
/*
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
const int mod = 998244353;
int n, m, num, lim, k, a[N], fst[N], tot, ifst[N], itot;
int _k, _a[N], vis[N], cnt, banx[N], bany[N];
int ft[N], fa[N][18], dfn[N], tim, dep[N], sta[N], top;
ll f[N][2], g[N][2], coe[2][N][2], ans;
struct edge {
int nxt, to;
} e[N << 1], ie[N << 1];
inline int read() {
char ch = getchar();
int s = 0, w = 1;
while (ch < '0' || ch > '9') {if(ch == '-') w = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {s = (s << 3) + (s << 1) + ch - '0'; ch = getchar();}
return s * w;
}
inline int find(int x) {
if (ft[x] == x) return ft[x];
return ft[x] = find(ft[x]);
}
inline void add(int u, int v) {
e[++tot] = (edge) {fst[u], v};
fst[u] = tot;
}
inline void iadd(int u, int v) {
ie[++itot] = (edge) {ifst[u], v};
ifst[u] = itot;
}
inline void dfs1(int u, int fth) {
dep[u] = dep[fth] + 1;
dfn[u] = ++tim; fa[u][0] = fth;
for (int i = 1; i <= 17; ++i) {
fa[u][i] = fa[fa[u][i - 1]][i - 1];
}
for (int i = fst[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (v == fth) continue;
dfs1(v, u);
vis[u] += vis[v];//要记得互相影响但是不在虚树上的点也不能遍历
}
}
inline int lca(int u, int v) {
if (dep[u] < dep[v]) swap(u, v);
for (int i = 17; ~i; --i) {
if (dep[fa[u][i]] >= dep[v]) {
u = fa[u][i];
}
}
if (u == v) return v;
for (int i = 17; ~i; --i) {
if(fa[u][i] != fa[v][i]) {
u = fa[u][i]; v = fa[v][i];
}
}
return fa[u][0];
}
inline bool cmp(int x, int y) {
return dfn[x] < dfn[y];
}
inline void IllusoryTree() {
_k = k;
for (int i = 1; i <= k; ++i) _a[i] = a[i];
sort(a + 1, a + 1 + k, cmp);
sta[top = 1] = 1; ifst[1] = 0;
for (int i = 1; i <= k; ++i) {
if (a[i] == 1) continue;
int Lca = lca(sta[top], a[i]);
if (sta[top] != Lca) {
while (dfn[sta[top - 1]] > dfn[Lca]) {
iadd(sta[top - 1], sta[top]); --top;
}
if (sta[top - 1] == Lca) {
iadd(sta[top - 1], sta[top]); --top;
}
else {
_a[++_k] = Lca;
vis[Lca] = 1;
ifst[Lca] = 0;
iadd(Lca, sta[top]);
sta[top] = Lca;
}
}
sta[++top] = a[i]; ifst[a[i]] = 0;
}
for (int i = 1; i < top; ++i) {
if (!vis[sta[i]]) {
_a[++_k] = sta[i];
vis[sta[i]] = 1;
}
iadd(sta[i], sta[i + 1]);
}
for (int i = 1; i <= _k; ++i) a[i] = _a[i];
k = _k;
}
inline void dp_init(int u, int fth) {
g[u][0] = g[u][1] = 1;
for (int i = fst[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (v == fth || vis[v]) continue;
dp_init(v, u);
(g[u][0] *= (g[v][0] + g[v][1])) %= mod;
(g[u][1] *= g[v][0]) %= mod;
}
}
inline void dp_help(int u, int son) {
f[u][0] = f[u][1] = 1;
for (int i = fst[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (v == son || v == fa[u][0]) continue;
dp_help(v, u);
(f[u][0] *= (f[v][0] + f[v][1])) %= mod;
(f[u][1] *= f[v][0]) %= mod;
}
}
inline void calc_coe(int u, int fth) {
int p = u;
coe[0][u][0] = coe[0][u][1] = coe[1][u][0] = 1;
while (fa[p][0] != fth) {
int q = fa[p][0];
dp_help(q, p);
ll coe00 = coe[0][u][0], coe01 = coe[0][u][1];
ll coe10 = coe[1][u][0], coe11 = coe[1][u][1];
coe[0][u][0] = (coe00 * f[q][0] + coe10 * f[q][1]) % mod;
coe[1][u][0] = coe00 * f[q][0] % mod;
coe[0][u][1] = (coe01 * f[q][0] + coe11 * f[q][1]) % mod;
coe[1][u][1] = coe01 * f[q][0] % mod;
p = q;
}
}
inline void dfs2(int u, int fth) {
dp_init(u, fth); a[++k] = u; vis[u] = 1;
if (u != fth) calc_coe(u, fth);
for (int i = ifst[u]; i; i = ie[i].nxt) {
int v = ie[i].to;
if (v == fth) continue;
dfs2(v, u);
}
}
inline void dp_calc(int u, int fth) {
for (int i = ifst[u]; i; i = ie[i].nxt) {
int v = ie[i].to;
if (v == fth) continue;
dp_calc(v, u);
(f[u][0] *= (coe[0][v][0] * f[v][0] + coe[0][v][1] * f[v][1]) % mod) %= mod;
(f[u][1] *= (coe[1][v][0] * f[v][0] + coe[1][v][1] * f[v][1]) % mod) %= mod;
}
}
int main() {
n = read(); m = read();
num = m - n + 1; lim = (1 << num);
for (int i = 1; i <= n; ++i) ft[i] = i;
for (int i = 1; i <= m; ++i) {
int u = read(), v = read();
int x = find(u), y = find(v);
if (x != y) {
add(u, v); add(v, u);
ft[x] = y;
}
else {
if (!vis[u]) a[++k] = u, vis[u] = 1;
if (!vis[v]) a[++k] = v, vis[v] = 1;
banx[++cnt] = u; bany[cnt] = v;
}
}
dfs1(1, 1);
IllusoryTree();
k = 0;
dfs2(1, 1);
/*if (!k) a[++k] = 1, vis[1] = k;
sort(a + 1, a + 1 + k, cmp);*/
for (int i = 0; i < lim; ++i) {
for (int j = 1; j <= k; ++j) {
f[a[j]][0] = g[a[j]][0];
f[a[j]][1] = g[a[j]][1];
}
for (int j = 1; j <= cnt; ++j) {
if ((1 << (j - 1)) & i) {
f[banx[j]][0] = 0;
f[bany[j]][1] = 0;
}
else f[banx[j]][1] = 0;
}
dp_calc(1, 0);
ans += f[1][0] + f[1][1];
}
printf("%lld\n", ans % mod);
return 0;
}

