[JLOI2016]方
(9.15 Update:把至少一个点被删掉的数量补充了一下,我是绝对不会告诉你我是因为懒才过了这么久才来修改的)
(注:本题解废话有点多,希望能写的能通俗易懂点
Description
在一个 \(n\) 行 \(m\) 列的方格图上,有 \(k\) 个点被删掉了,问剩下的点能构成多少个三角形。
\(0\leq n,\ m \leq 10^6\) , \(0\leq k \leq 2\cdot 10^3\)
Analysis
题意大概就是问由所有点构成的所有正方形中,
有多少个是其四个顶点都没被删掉的。
直接做似乎不太行,可以想想算答案的补集。
一个正方形的话,只要枚举两个点,就可以算得这两个点所在的唯三的正方形。
给个图:
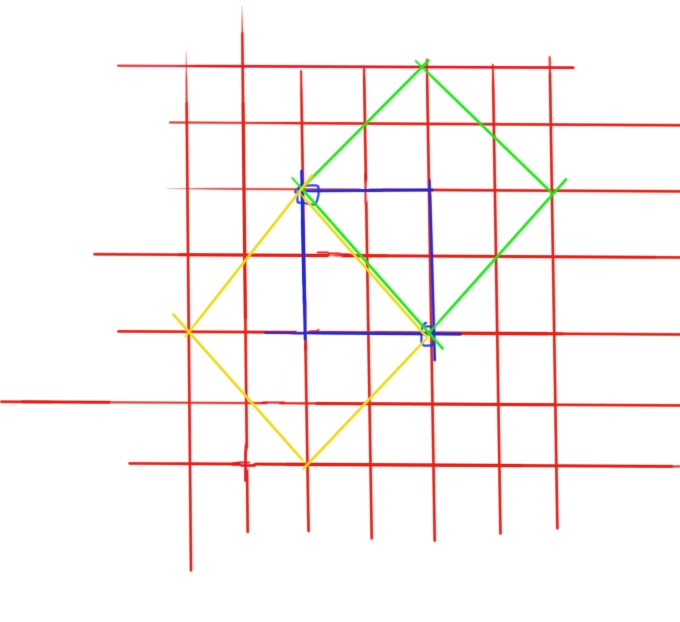
所以算答案的补集的话,选择枚举被删掉了的点,复杂度上是非常合适的。
所以基本可以确定,答题思路应该跟 \(O(k^2)\) 枚举有密切联系。
现在再来看看补集要干什么。
无非就是一个点被删去的正方形,两个的,三个的以及四个的数量总和。
但是发现这个枚举枚举,不能做一个点的情况,如果要做的话好像也不太行。。
再想想怎么避免掉。
其实这样直接求的话,本质上我们要考虑的地方除了枚举的点,还有其他三个点的情况。
所以我们可以考虑一个简单的容斥,把求的东西全部改成至少有( 1-4 )个点被删掉的正方形的数量。
这样求的时候,也只去大胆的枚举就行了。
看起来很可做的样子!
Solution
至少零个点被删掉的正方形数量(总方案数)
直接算好像也不行,所以可以考虑一系列的正方形可能存在什么样的类似的特征。
比如斜着的正方形能“圈起来”。
给个图:
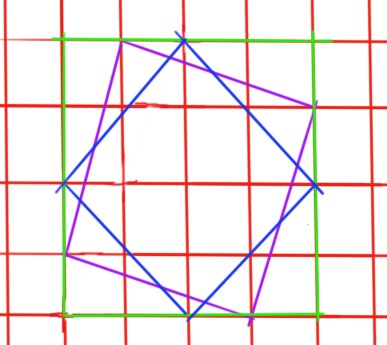
发现一个“圈”能圈住好多正方形,大小相同的正方形能圈住的数量又都是一样的。
所以枚举“圈”的大小 \(O(\min(n, m))\) 就可以算了。
至少一个点被删掉的正方形数量
因为只要找一个点,所以也只要枚举一个点就可以了。
对于每个被删去的点,以它为原点向四周找到一个新正方形对角线上的点,分成与该点同纵坐标或横坐标和其他点分类统计,然后加起来就是合法个数了。
注意下这个其他点中有斜的不太正常的那种(比如上图中紫色那个)。
这种情况是在对角线横纵坐标差同奇偶的时候。
因为只有这样另一条对角线才能稳稳的落在两个点上而不是悬在空中。
来实操一下,分两种情况:
1. 在该点上下左右的两条直线上
以下面半边为例,给个图:
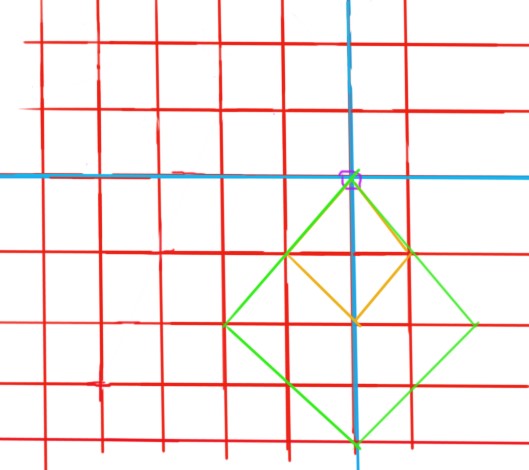
可以看到,线上只有距点偶数距离的存在正方形。同时,绿色那个正方形,由于右边超出边界,也不合法。
类比此做法,可以把上下左右都搞定。
2. 其他
前面有给到一个合法正方形的条件,那么,
以左下角为例,再给个图:
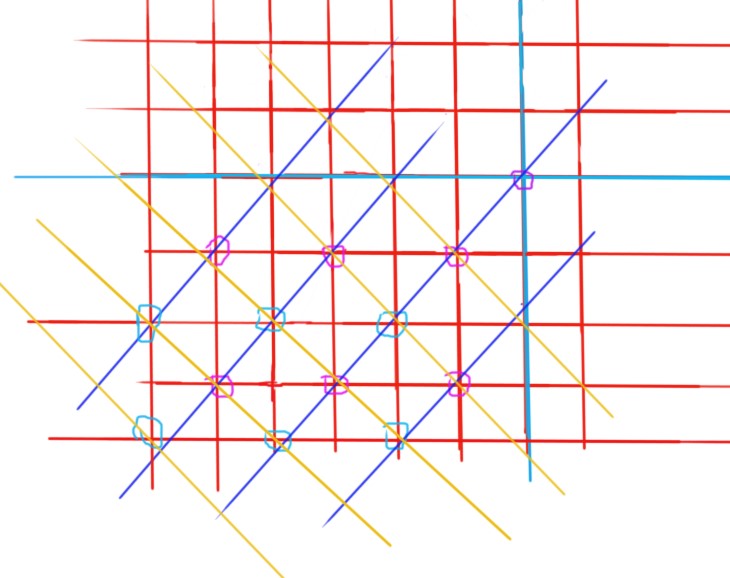
先抛开那些斜线不谈,圈起来的点就是所有能构成正方形的点们(粉紫色均为奇数,淡蓝色均为偶数)
全部把正方形复原出来后,会发现有些已经超出了边界,也就是不合法的了。
那么,什么情况下的点是不合法的呢?
1.第一类是像最左下角的那个蓝点,复原出来的话下方的点显然是出了自家的大门。
如果左边还有点,对应的最下面的黄色的斜线上的点同样都不合法,所以这些不合法的点都被“绑定”到了一起。
2.第二类同理,分两个方向,一个右下角,一个左上角,但此图两者都是压线,没有不合法的。
感性理解的话,还是一样,不合法的点都被“绑定”到了蓝色的斜线上。
于是,不合法的点“绑定”起来的话,也就更方便于计算。
但是,同时我们还应该要想到这样会不会需要容斥,
如果两类不合法点有交集,那么就相当于这样:
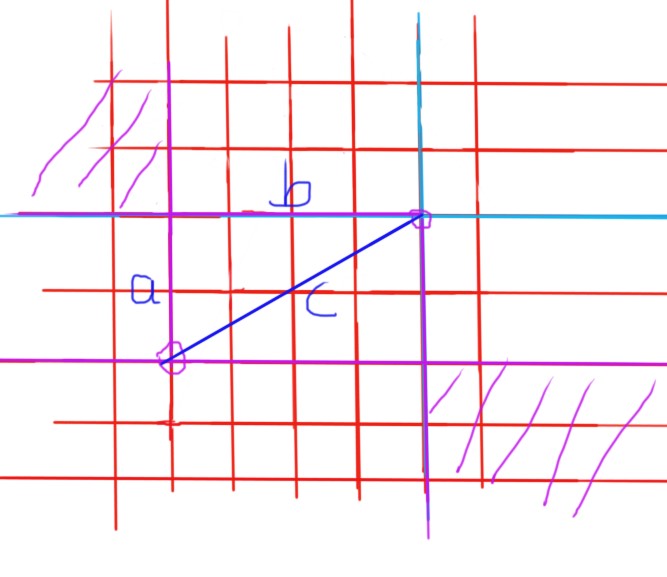
可以看到,点要出现在超出两个边界的两块紫色阴影才有可能出现同为两类不合法点的情况。
但是稍稍想一下,这里 \(a^2+b^2=c^2\) ,但是我们复原出来的正方形边长也是 \(p^2+p^2=c^2\) ,很显然是没有 \(p>a\) 且 \(p>b\) 的情况,也就不用想容斥了。
至少二,三,四个点被删掉的正方形数量
先枚举,对于存在的三个正方形,要先判断这三个正方形合不合法,因为有可能有的正方形坐标不合法,或者,
再给个图:
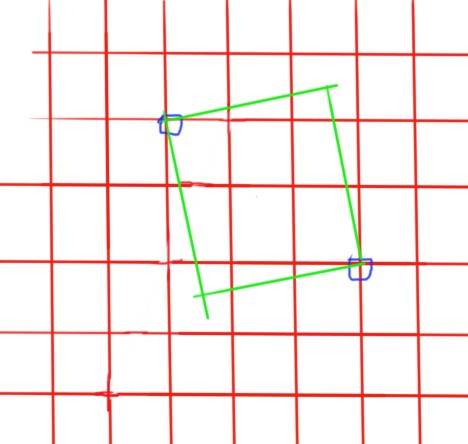
这玩意显然不对呀!
排除掉不合法的正方形后就能直接算了。
但其实这样子的答案样例都过不了。。
所以还要再想想直接这样算对不对,
盯着这张图:
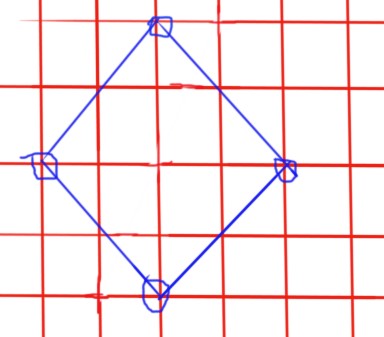
可以发现如果只有两个点被删掉了,那么枚举的时候,
会对至少两个的数量贡献 1 ,没有问题。
如果是三个点的话,这个正方形会被枚举 \(C_3^2 = 3\) 次,其中,
会对至少两个的数量贡献 3 ,没有问题。
会对至少三个的数量贡献 3 ,那一种方案被算了 3 次。
如果是四个点的话,这个正方形会被枚举 \(C_4^2 = 6\) 次,其中,
会对至少两个的数量贡献 6 ,没有问题。
会对至少三个的数量贡献 12 ,四种方案都被算了 3 次。
会对至少两个的数量贡献 6 ,那一种方案被算了 6 次。
所以最后算出来的至少三个的数量除以 3 ,至少四个的数量除以 6 ,就算搞定整个题目了。
Attention
存坐标是否被删去不能数组存,所以要开 map 或 set !所以时间复杂度为 \(O(k^2\log(nm))\) ,只有 50 分。
所以要用 unordered_map 或 unordered_set ,时间复杂度 \(O(k^2)\) ,就能拿到 100 啦。
Code
#include<bits/stdc++.h>
#define id(i, j) i * (m + 1) + j + 1
using namespace std;
typedef long long ll;
const int N = 1e6 + 10, M = 2e3 + 10;
const ll mod = 1e8 + 7;
ll n, m, k, zer, sig, dou, tri, qua, ans;
struct mdzz {
ll u, v;
} p[N];
unordered_set<ll> vis;
inline ll read() {
ll s = 0, w = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {if (ch == '-') w = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {s = (s << 3) + (s << 1) + ch - '0'; ch = getchar();}
return s * w;
}
inline int mul(int a, int b) {
return (1ll * a * b) % mod;
}
inline int pd(ll zb) {
return vis.find(zb) != vis.end();
}
inline void ans_zero() {
int lim = min(n, m);
for (int i = 1; i <= lim; ++i) {
zer = (zer + mul(i, mul(n - i + 1, m - i + 1))) % mod;
}
}
inline int anslrh(int l ,int r, int h) {
int t = min(l + r, h);
if (!t) return 0;
int ret = (1ll * t * (t + 3) >> 1ll) % mod;
if (t > l) ret = (ret - (1ll * (t - l) * (t - l + 1) >> 1) % mod + mod);
if (t > r) ret = (ret - (1ll * (t - r) * (t - r + 1) >> 1) % mod + mod);
return ret % mod;
}
inline void ans_single(mdzz x) {
int a = x.u, b = x.v, c = n - x.u, d = m - x.v;
sig += (anslrh(a, c, b) + anslrh(a, c, d)) % mod;
sig += (anslrh(b, d, a) + anslrh(b, d, c)) % mod;
sig = (sig - (min(a, b) + min(b, c) + min(c, d) + min(d, a)) % mod) % mod;
}
inline int check_double(mdzz x, mdzz y) {
if (x.u < 0 || y.u < 0 || x.v < 0 || y.v < 0) return 0;
if (x.u > n || y.u > n || x.v > m || y.v > m) return 0;
return 1;
}
inline void ans_double(mdzz x, mdzz y) {
int d1 = y.u - x.u, d2 = x.v - y.v;
mdzz a1 = x, b1 = y; a1.u += d2; a1.v += d1; b1.u += d2; b1.v += d1;
mdzz a2 = x, b2 = y; a2.u -= d2; a2.v -= d1; b2.u -= d2; b2.v -= d1;
dou += check_double(a1, b1) + check_double(a2, b2);
int d3 = (x.u + y.u), d4 = (x.v + y.v);
mdzz mid = (mdzz) {d3, d4};
mdzz a3 = mid, b3 = mid; a3.u += d2; a3.v += d1; b3.u -= d2; b3.v -= d1;
if ((a3.u & 1) || (a3.v & 1)) return ;
if ((b3.u & 1) || (b3.v & 1)) return ;
a3.u /= 2; a3.v /= 2; b3.u /= 2; b3.v /= 2;
dou += check_double(a3, b3);
}
inline int check_triple(mdzz x, mdzz y) {
if (x.u < 0 || y.u < 0 || x.v < 0 || y.v < 0) return 0;
if (x.u > n || y.u > n || x.v > m || y.v > m) return 0;
return pd(id(x.u, x.v)) + pd(id(y.u, y.v));
}
inline void ans_triple(mdzz x, mdzz y) {
int d1 = y.u - x.u, d2 = x.v - y.v;
mdzz a1 = x, b1 = y; a1.u += d2; a1.v += d1; b1.u += d2; b1.v += d1;
mdzz a2 = x, b2 = y; a2.u -= d2; a2.v -= d1; b2.u -= d2; b2.v -= d1;
tri += check_triple(a1, b1) + check_triple(a2, b2);
int d3 = (x.u + y.u), d4 = (x.v + y.v);
mdzz mid = (mdzz) {d3, d4};
mdzz a3 = mid, b3 = mid; a3.u += d2; a3.v += d1; b3.u -= d2; b3.v -= d1;
if ((a3.u & 1) || (a3.v & 1)) return ;
if ((b3.u & 1) || (b3.v & 1)) return ;
a3.u /= 2; a3.v /= 2; b3.u /= 2; b3.v /= 2;
tri += check_triple(a3, b3);
}
inline int check_quadruple(mdzz x, mdzz y) {
if (x.u < 0 || y.u < 0 || x.v < 0 || y.v < 0) return 0;
if (x.u > n || y.u > n || x.v > m || y.v > m) return 0;
return pd(id(x.u, x.v)) & pd(id(y.u, y.v));
}
inline void ans_quadruple(mdzz x, mdzz y) {
int d1 = y.u - x.u, d2 = x.v - y.v;
mdzz a1 = x, b1 = y; a1.u += d2; a1.v += d1; b1.u += d2; b1.v += d1;
mdzz a2 = x, b2 = y; a2.u -= d2; a2.v -= d1; b2.u -= d2; b2.v -= d1;
qua += check_quadruple(a1, b1) + check_quadruple(a2, b2);
int d3 = (x.u + y.u), d4 = (x.v + y.v);
mdzz mid = (mdzz) {d3, d4};
mdzz a3 = mid, b3 = mid; a3.u += d2; a3.v += d1; b3.u -= d2; b3.v -= d1;
if ((a3.u & 1) || (a3.v & 1)) return ;
if ((b3.u & 1) || (b3.v & 1)) return ;
a3.u /= 2; a3.v /= 2; b3.u /= 2; b3.v /= 2;
qua += check_quadruple(a3, b3);
}
int main() {
// freopen("square.in", "r", stdin);
// freopen("sqyare.out", "w", stdout);
n = read(); m = read(); k = read();
for (int i = 1; i <= k; ++i) {
int u = read(), v = read();
p[i] = (mdzz) {u, v};
vis.insert(id(u, v));
}
ans_zero();
for (int i = 1; i <= k; ++i) {
ans_single(p[i]);
for (int j = i + 1; j <= k; ++j) {
ans_double(p[i], p[j]);
ans_triple(p[i], p[j]);
ans_quadruple(p[i], p[j]);
}
}
tri /=3; qua /= 6;
dou %= mod; tri %= mod; qua %= mod;
printf("%lld\n", (zer - sig + dou - tri + qua + mod + mod) % mod);
return 0;
}

