【模板】支配树
看了许多大佬的讲解,就用自己的语言说一遍,可能讲得不好(毕竟还是太菜了)
Description
给定一张有向图,求从起点出发,求所有点再去掉的情况下有多少个点到达不了(就是支配点的概念)。
\(n\leq 2\cdot10^5\) , \(m\leq 3\cdot 10^5\)
Prepose content
根据题目,我们以此来建一个树,称之为“支配树”
满足“支配树”要满足这些性质:
1.这是一个树(而不是图),根节点就是起点;
2.对于任意点 \(u\) ,从根到它的简单路径上的所有点都是它的支配点;
3.对于任意点 \(u\) ,它支配它的子树上所有的子孙节点。
如果能这样造出来,问题就解决了。
Prepose algorithm
\(Lengauer-Tarjan\) 算法
哪里都有 Tarjan 老爷子。。。 Tarjan orz !
\(Lengauer-Tarjan\) 算法主要分了三个步骤:
1.从起点开始造 \(dfs\) 树并求出所有点的 \(dfn\) ;
2.求出所有点的半支配点;(暂设数组 \(semi(i)\) )
3.求出所有点的支配点。(暂设数组 \(idom(i)\) )
其中半支配点是一个新概念,也是间接求支配点的精髓。
对于任意点 \(u\) 的半支配点表示所有点中有 dfn 最小的点 \(v\) ,能使 \(v\) 满足有一条路径能够到达 u 且路径上的所有点( \(u\) 和 \(v\) 都不算)的 \(dfn\) 都大于 \(dfn(u)\) 。
Mainly content
就只讲讲一般有向图吧,因为这个解决了其他的就都解决了(如树, DAG )。
half-Dominant
设目前我们在研究点 \(u\) ,那么再设点 \(v\) 指所有直接连向 \(u\) 的点。
分类讨论(王道!)
1.\(dfn(v)=dfn(u)\)
直接无解。。跳过。
2.\(dfn(v)<dfn(u)\)
如果要从这条路径上走的话,刚开始就结束了(根据定义来),所以把 \(v\) 和可能存在的 \(semi(u)\) 择优更新就好了。
3.\(dfn(v)>dfn(u)\)
那么就在 \(dfs\) 树上从 \(v\) 找一个祖先 \(w\) 且 \(dfn(w)>dfn(u)\) ,然后就把可能存在的 \(semi(w)\) 和可能存在的 \(semi(u)\) 择优更新。
因为既然有了 \(semi(w)\) ,这一段路径上所有 \(dfn\) 都大于 \(dfn(u)\) (定义来的), \(w\) 又是从 \(semi(u)\) 到 \(u\) 的路径上搜到的,所以 \(w\) 之后的点也满足。
(不是很懂??正常,我也有点云里雾里的(就算明白了,一会也就忘了),但关键好背!!)
至此,半支配点完结!
Dominant
考虑在半支配点的肩膀上求出支配点。
设目前我们在研究点 \(u\) 。
然后记一个点集 \(\large\xi\) 表示在 \(dfs\) 树上从 \(semi(u)\) 到 \(u\) 的路径的点集,(但不包括 \(semi(u)\) )其中点 \(\alpha\) 是 \(\large\xi\) 中 \(dfn(semi)\) 最小的点。
那么,分类讨论(王道!)
(肯定是判断 \(semi\) 相等而不是比较 \(dfn\) 大小了呀)
1.\(semi(\alpha)=semi(u)\)
则 \(idom(u)=semi(u)\) 。
因为 \(\alpha\) 已经是 \(semi(u)\) 到 \(u\) 路径中所有点的下限( \(dfn(semi)\) )了,如若当前情况就是 \(\large\xi\) 成了个封闭的点集, \(semi(u)\) 是唯一直接相连的点,自然就有了 \(idom(u)=semi(u)\) 。
2.\(semi(\alpha)\neq semi(u)\)
则 \(idom(u)=idom(\alpha)\) 。
感性理解:
倘若有这么一个“中间点” \(\beta\) 。
我们假设没有了 \(idom(\alpha)\) , \(u\) 还可以能够到达。那么说明 \(idom(\alpha)\) 祖先会有一个点有一条非 \(dfs\) 树边连向了 \(idom(\alpha)\) 和 \(u\) 中间的一个点 \(\beta\) 。
其中, \(\alpha\) 必是 \(\beta\) 的祖先,否则没有了 \(idom(\alpha)\) 也能到达 \(\alpha\) ,显然与定义不符。
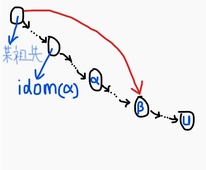
如若如此, \(\beta\) 便一定在 \(\large\xi\) 中了。
看得出来, \(semi\) 的要求比 \(idom\) 高一些,从满足条件的难度上,所以 \(dfn(idom(\alpha))\leq dfn(semi(\alpha))\) 显然。(记住,这是感性。。)
但 \(idom(\alpha)\) 的祖先有一条非 \(dfs\) 树边连向了 \(\beta\) ,所以无论如何 \(dfn(semi(\beta))<dfn(idom(\alpha))\) 。
结合上面的两段内容,发现会与 \(\large\xi\) 关于 \(\alpha\) 的定义不符了。所以没有了 \(idom(\alpha)\) , \(u\) 一定不能够到达。
至此,支配点完结!
Solution
1.半支配点
如果还有点印象的话,应该能知道求解过程都是 dfn 从大到小的逆推,所以可以倒序 dfn 处理。
对于第二个情况(第一个就。。)直接干,而第三种情况,肯定是不会暴力枚举的。
于是考虑一个带权并查集(说的好像要怎么样,但代码就是好背),每次处理完一个点,就往它在 dfs 树上的点合并,按照支配点中 \(\large\xi\) 的要求维护对应的东西。
2.支配点
很多辅助东西都与半支配点一并整好了,只需要把已经求的 semi 与对应的点连边,构造半支配树,就能同时求解支配点。
由于可能存在搜索的时候 idom 并未找到,可以先记录下来,最后顺序 dfn 再额外处理。
有一个小注意可见这位大佬在代码上方的讲述。
时间复杂度 \(O(n\log_{2}{n})\) ,优雅的诠释了\(Lengauer-Tarjan\) 算法的优越性。
(没办法, Tarjan 老爷子就这么厉害。。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+10,M=3e5+10;
int n,m,ans[N],tot;
int fst[N][3],nxt[M+M+N],to[M+M+N];
int dfn[N],ord[N],cnt,fth[N];
int idom[N],semi[N],uni[N],mn[N];
inline ll read()
{
ll s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
inline void add(int u,int v,int id)
{
nxt[++tot]=fst[u][id];
to[tot]=v,fst[u][id]=tot;
}
inline void Tarjan(int u)
{
ord[dfn[u]=++cnt]=u;
for(int i=fst[u][0];i;i=nxt[i])
{
int v=to[i];
if(!dfn[v])
{
fth[v]=u;
Tarjan(v);
}
}
}
inline int uni_query(int u)
{
if(u==uni[u])return u;
int tmp=uni_query(uni[u]);
if(dfn[semi[mn[u]]]>dfn[semi[mn[uni[u]]]])mn[u]=mn[uni[u]];
return uni[u]=tmp;
}
inline void Lengauer_Tarjan(int s)
{
Tarjan(s);
for(int i=1;i<=n;++i)semi[i]=uni[i]=mn[i]=i;
for(int id=cnt;id>=2;--id)
{
int u=ord[id];
for(int i=fst[u][1];i;i=nxt[i])
{
int v=to[i];
if(!dfn[v])continue;
uni_query(v);
if(dfn[semi[u]]>dfn[semi[mn[v]]])semi[u]=semi[mn[v]];
}
uni[u]=fth[u];
add(semi[u],u,2);
u=fth[u];
for(int i=fst[u][2];i;i=nxt[i])
{
int v=to[i];
uni_query(v);
idom[v]=(u==semi[mn[v]]?u:mn[v]);
}
fst[u][2]=0;
}
for(int i=2;i<=cnt;++i)
{
int u=ord[i];
if(idom[u]^semi[u])
idom[u]=idom[idom[u]];
}
}
int main()
{
n=read(),m=read();
for(int i=1;i<=m;++i)
{
int x=read(),y=read();
add(x,y,0),add(y,x,1);
}
Lengauer_Tarjan(1);
for(int i=cnt;i>=2;--i)ans[idom[ord[i]]]+=(++ans[ord[i]]);
++ans[1];
for(int i=1;i<=n;++i)printf("%d ",ans[i]);
return 0;
}
完结撒花!

