组合数学随笔(更新中)
组合数学的笔记
基本公式:
\(\mathrm C_n^m = \frac{n!}{m! \times (n-m)!}\)
\(\mathrm A_n^m = \frac{n!}{(n-m)!}\)
组合数学9题:
1.不同球n,不同盒子m,可为空,全放入方案数:
每个球m种方法,\(ans = m^n\)
2.不同球,不同盒,不可为空
先思考不同球,相同盒子,不可为空
设\(f[n][m]\)为方案数,那么对于一个球而言,可以选择放入前面放过的盒子,也可以新开一个,所以有:
\(f[n][m] = f[n-1][m] \times m + f[n-1][m-1]\)
边界条件:\(f[n][1] = 1,f[n][n]=1\)
那么只要把\(f[n][m]\)乘上m的排列数就好了
\(ans = f[n][m] \times m!\)
3.相同球,不同盒子,可为空
先思考不可为空,
那么看作有n个球,\(n-1\)个缝,选\(m-1\)个把板插进去
\(ans=\mathrm C_{n-1}^{m-1}\)
然后可为空,相当于多放m个球在每个盒子里,再放n个球
转换为:\(ans=\mathrm C_{n+m-1}^{m-1}\)
4.相同球,不同盒子,不可为空
见3
5.不同球,相同盒子,可为空
在2中提过\(f[n][m]\)为不可为空的方案数,那么相当于不为空放一个盒子+不为空放两个盒子+....+不为空放m个盒子
转换为:\(ans=\sum_{i=1}^m f[n][i]\)
6.不同球,相同盒子,不可为空
见2
7.相同盒子、相同球,可为空
设\(g[n][m]\)为n个球,m个盒子的情况。
那么分成两种情况:有盒子为空,和无盒子为空
划分子问题,有盒子为空可划分为\(n,m-1\),没有盒子不为空可划分为\(n-m,m\)(每个盒子里先放一个)
那么\(g[n][m] = g[n][m-1] + g[n-m][m]\)
8.相同盒子,相同球,不为空
直接可得出答案就是7中的\(f[n-m][m]\)。
从八个组合问题得出的一些性质很棒的数:
斯特林数
第二类斯特林数
划分数
其他性质很棒的数
卡特兰数
给定一个凸\(n\)边形,用对角线(对角线不可相交)把它划分成三角形,问方案数(显然旋转后相同的两种方案都要算进去
接下来,思考划分子问题,容易想到把该多边形划分为两个多边形,但是发现如果用直线划分的话需要考虑很多重复的问题,于是用一个三角形把该多边形划分成两个三角形。
想到每个多边形中每一条边都属于一个三角形,那么被用来划分的三角形可以“依附”与一条固定的边上。然后剩下的一个点在多边形上移动,当那个点在下图中v3时,可划分为一个三角形和一个n-1边形(一共n+1条边)。然后不断移动未确定的点,就可以得到多种划分,缩减成不同子问题。再利用加分原理把这些情况加起来(并不会有重复,用来划分的三角形的确定的那条边在不同情况中属于的三角形一定不同)就可以得到最终解。
得到一个柿子:\(f[n]=\sum_{i=2}^{n-1}f[i]f[n-i+1]\)且\(f[2]=1\)
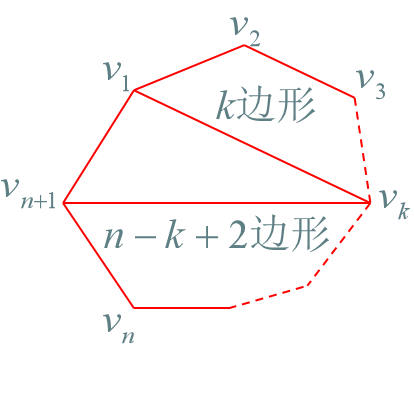
我们就得到了Catalan数的线性递推关系。
当然,在更多的情况里,卡特兰数一般是\(f[n]=\sum_{i=0}^{n-1}f[i]f[n-i-1]\)且\(f[0]=1,f[1]=1\),前后两个并没有什么区别,只是根据具体情况调整了边界而已。
然后是通项公式:\(f[n]=\frac{\mathrm C_{2n}^n}{n+1}\)
至于推导过程或证明,留坑(等我会了再说)。
贝尔数
相似于第二类卡特林数,意义为把\(n\)个元素划分为不同非空子集的方案数(集合数量可调整,元素不同)。
第二类斯特林数的递推式为\(f[n][m] = f[n-1][m-1] + f[n-1][m] * m\) 那么贝尔数便可以\(f[n][m]\)的基础上得来,\(B_n = \sum_{i=1}^{n}f[n][i]\)。
贝尔数\(B_n\)也可以从前面的项递推出来。方法如下:
将一个元素划分进来,构成\(B_{n+1}\)。
那么可以将它单独划分为一组,剩下\(n\)个元素划分,方案数为\(n\)的贝尔数\(B_n\)
若将这个新划分的元素可以与另一个任意的元素划分为一组,还剩任意的\(n-1\)个元素,那么方案数即是从\(n\)个元素挑选\(n-1\)个元素(也可以理解为挑选出1个和新划分的元素组成一组),求出它们的贝尔数\(B_{n-1}\)
若将这个新划分的元素与另外任意两个元素划分为一组,从\(n\)中挑选\(n-2\)个元素,并求出\(B_{n-2}\)。
以此类推,并使用加法原理加起来,递推式子是:\(B_{n+1} = \sum_{i=0}^{n}\mathrm C_{n}^iB_{i}\)
伯努利数
别的知识点
二项式定理
\(\sum_{k=1}^n{\mathrm C_{n}^{n-k}x^k}\)
其实该定理与二项式有联系,既是发现上面式子的值\(=(x+1)^k\),那么便可以使用在组合中所用甚广的杨辉三角来把它拆开,化简就是二项式定理。
十分重要的容斥原理
先回忆小学的时候学过的:
已知满足条件一的集合A,满足条件二的集合B
求两个集合的并集的大小。
答案就是\(|A+B|-|A\cap B|\)
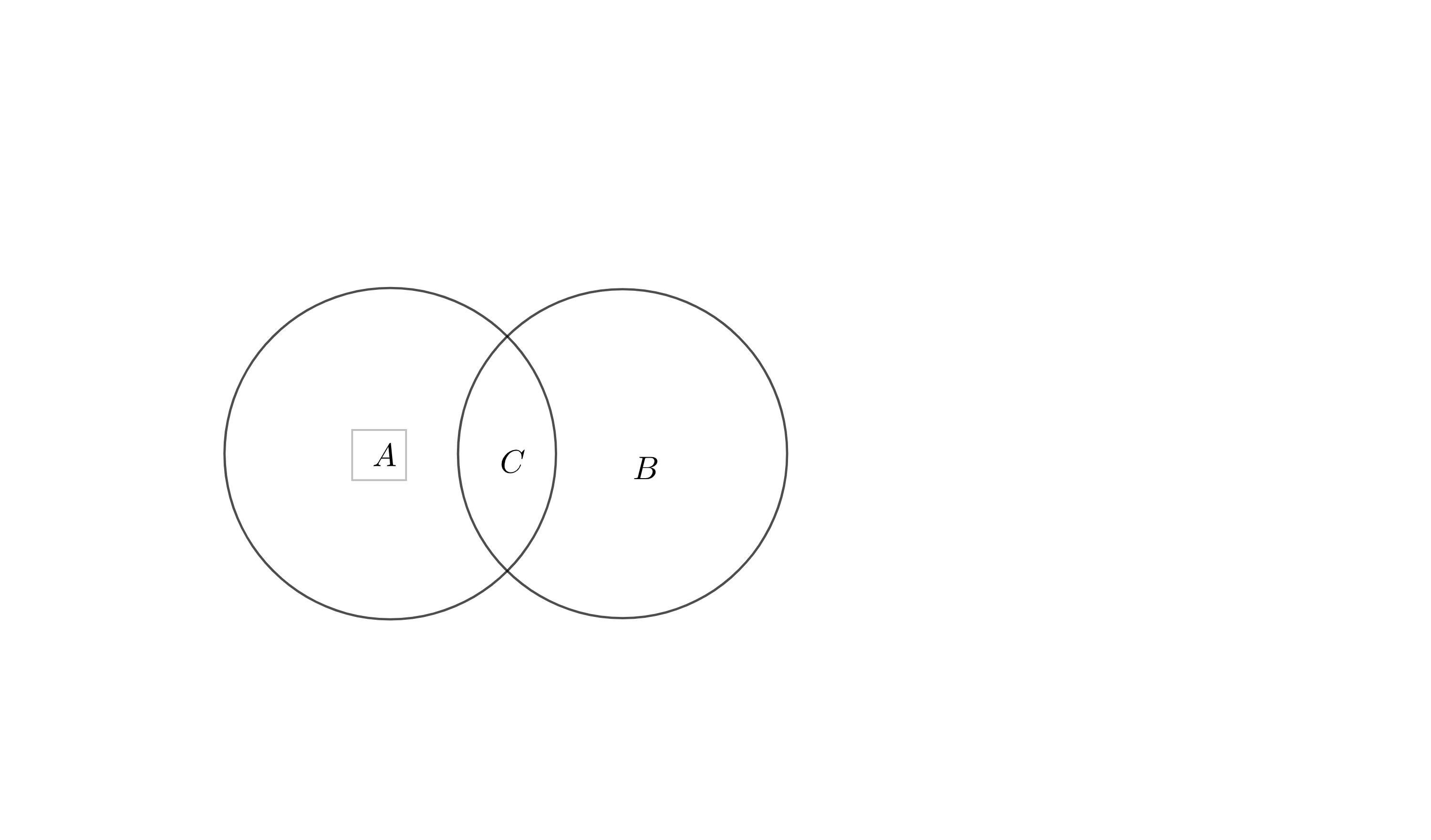
然后:\(|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A\cap C| - |B\cap C| + |A\cap B \cap C|\)
最终可以推广出:
\(|\bigcup_{i=1}^{n}A_i| = \sum_{j=1}^{n}(-1)^{j-1}\sum_{i<i+1}|\bigcap_{i=1}^{m}A_i|\)
其实就是先全加起来,减去重复一次的,加上重复两次的,减去重复三次的,加上重复四次的,以此类推。
至于更加深入与困难的容斥,暂不讨论(坑)。
一些模型
路径计数
问题一:
从点(0,0)到店(n,m),只可向上,向右\((n,m>0)\)
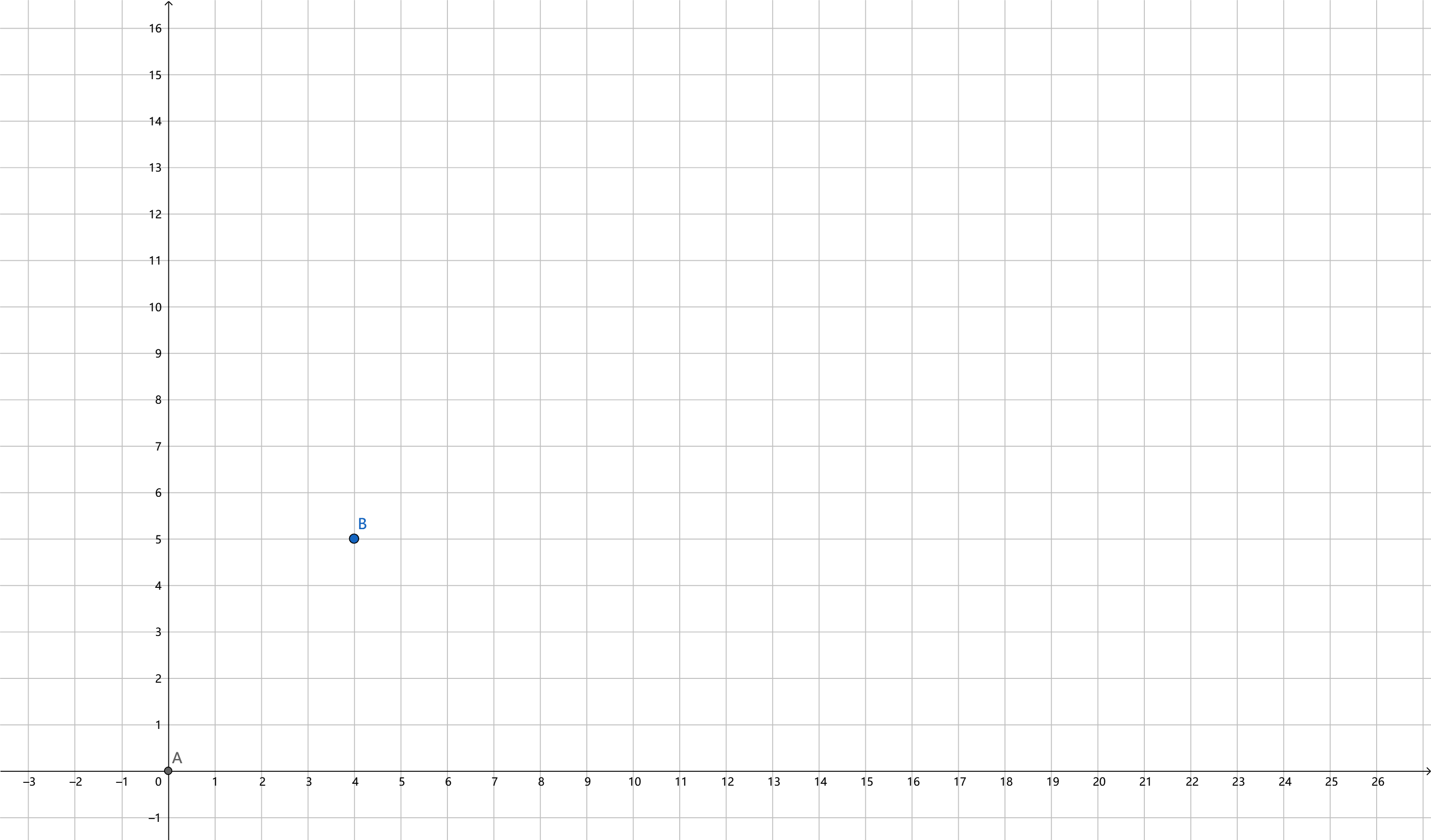
相当于向右走n次,向上走m次,那么答案相当于是走n+m次,选n次向右
\(ans=\mathrm C_{n+m}^{n}\)
问题二:
途中不能接触直线\(y=x\),从(0,0)到(n,n),七点与终点不算接触
相当于从(0,1)到(n,n-1)与从(1,0)到(n-1,n),我们先考虑一边,从(0,1)到(n,n-1)
不管有没有接触,走的方案数为:\(C_{2n-2}^{n-1}\)
再考虑接触,如果接触了,我们把接触,以及穿过直线后的图像直到回到直线一边的部分对称过去
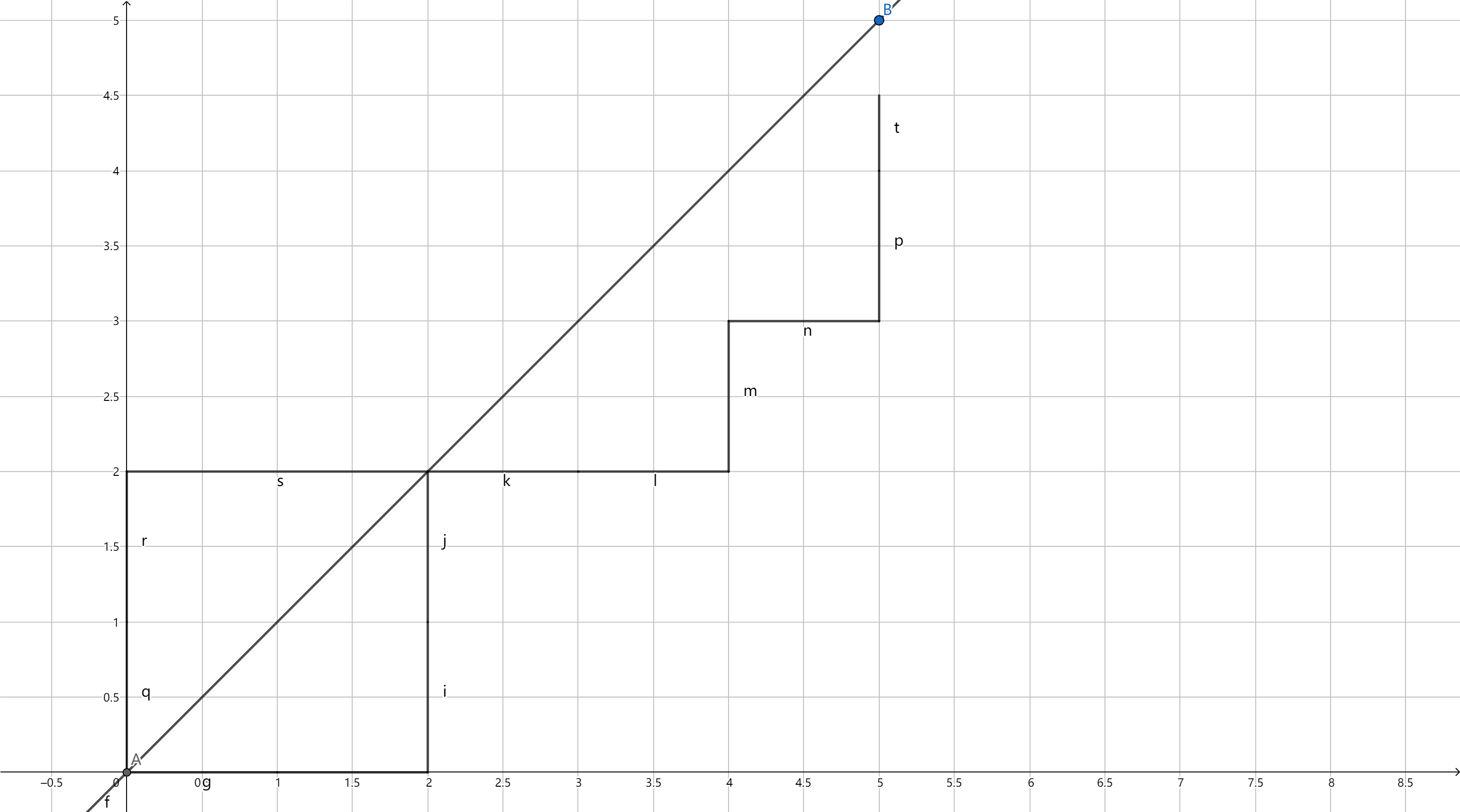
发现对称过去后的这一部分加上没有被对称的一部分刚好可以被表示为(1,0)到(n,n-1)的一条路径。推广一下,所有这样接触了的路径都可以与(1,0)到(n,n-1)的某条路径一一对应。那么我们只需要减去从(1,0)到(n,n-1)的所有路径就可以算出正确答案。
至于另一部分答案,对称一下即可。
\(ans = 2(\mathrm C_{2n-2}^{n-1}-\mathrm C_{2n-2}^{n})\)
这个模型其实与卡特兰数有些关系,将不可接触改为不可穿过,再只考虑一部分,就可以把该题变成一个卡特兰数的题目。并且,你也可以利用这个来推到卡特兰数的通项公式。

