图像特征-harris角点检测
转自：https://zhuanlan.zhihu.com/p/449970674
一 角点检测基本原理
角点： 沿着各个方向，图像灰度均发生变化的点，可认为是角点。
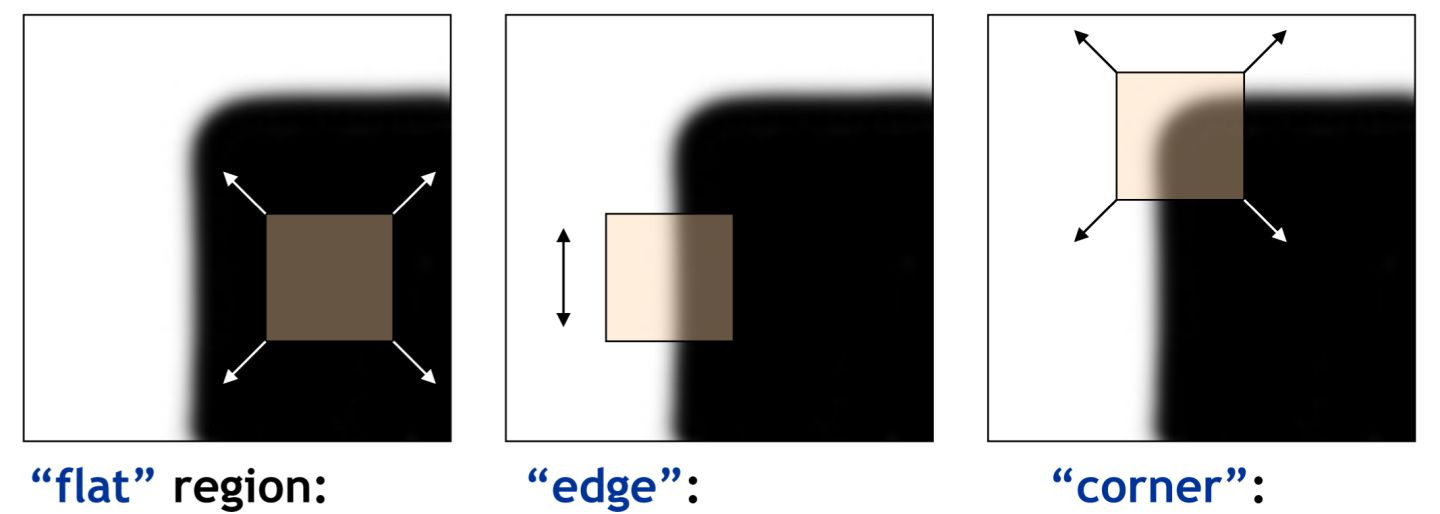
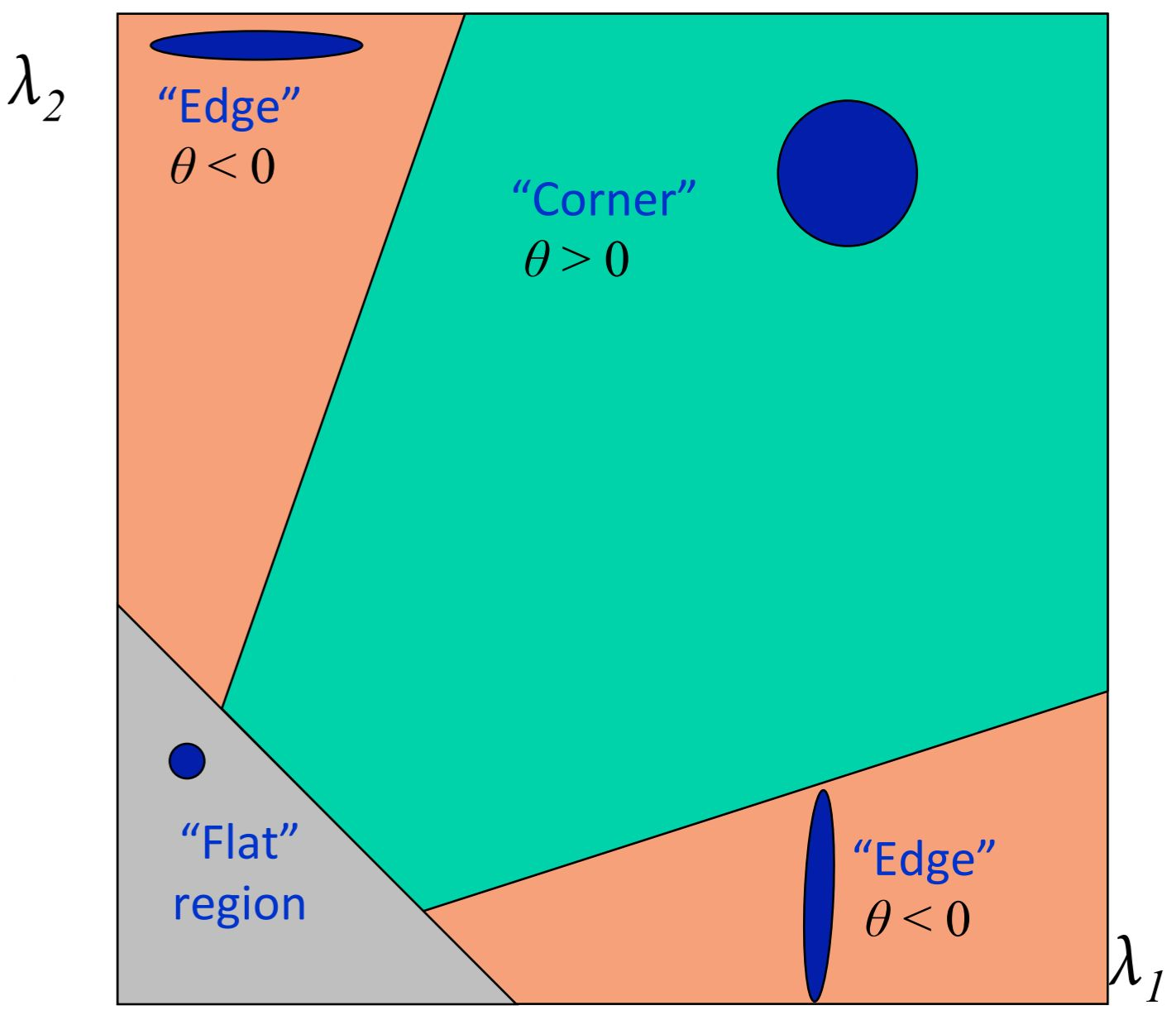
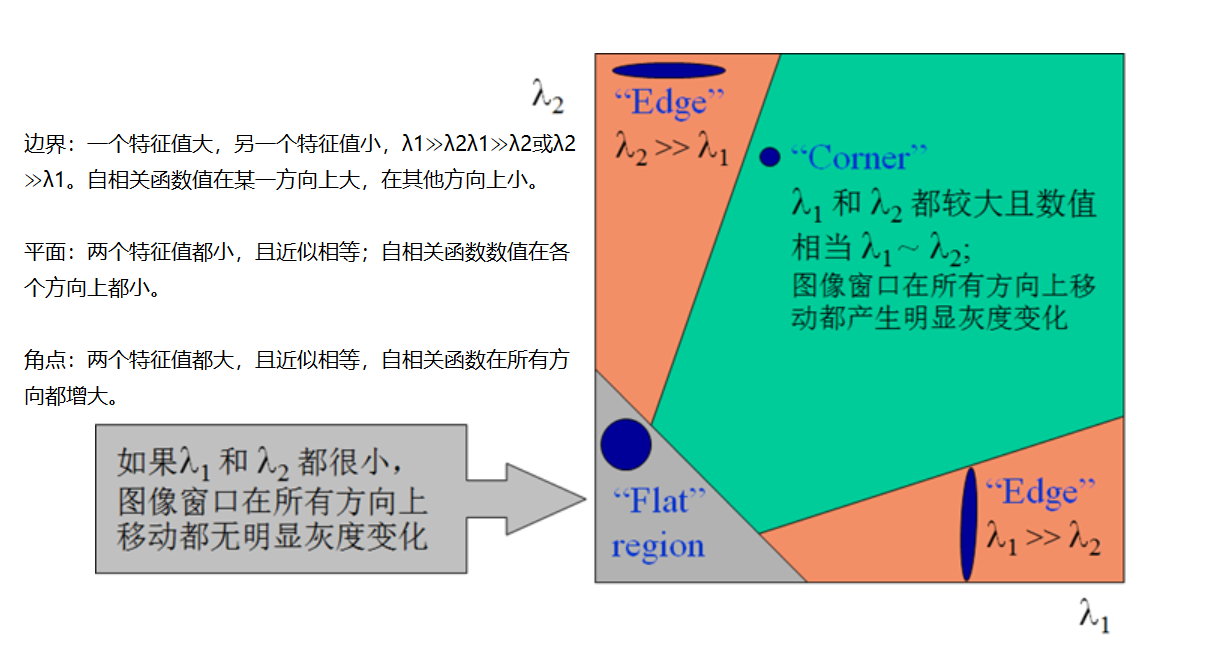
图像中三种可能的区域，“flat”、“edge”、“corner”；
- 平坦区域“flat region”，多个方向移动，平均亮度几乎没变化。
- 边缘“edge”，某个方向上亮度变化剧烈，而垂直的方向上变化很小。
- 角点“corner”，任意方向移动，平均亮度变化都很剧烈。
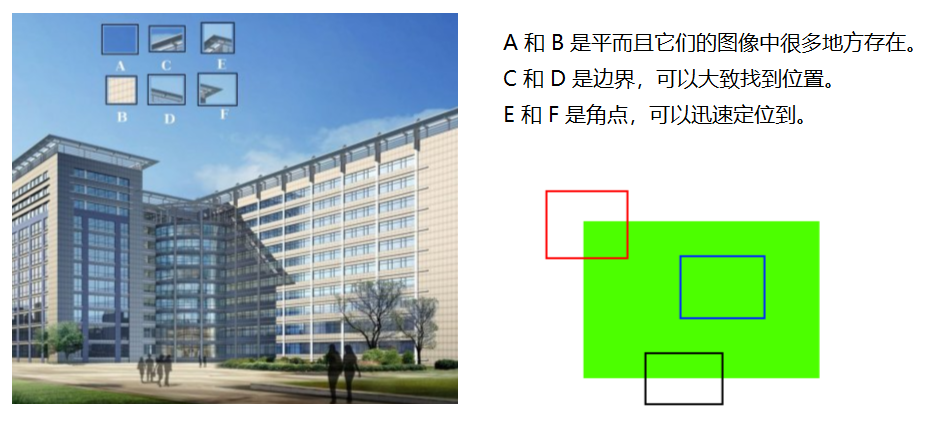
数学上怎么描述角点？
可以通过以下自相关函数来描述局部窗口的亮度变化，从而定义角点。
-
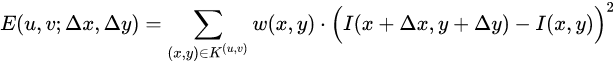
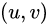代表当前待判定的点，其局部窗口为
； 
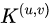分别是水平、垂直方向上的偏移量；
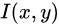代表图像I在点
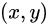的亮度值；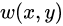
是局部窗口加权函数，有高斯加权和平均加权等，因为一般窗口的每个像素点贡献度是不一样的，因此需要乘以一个加权函数；
公式右边括号内即为局部窗口的灰度变化。
根据泰勒公式展开一阶近似后，有：
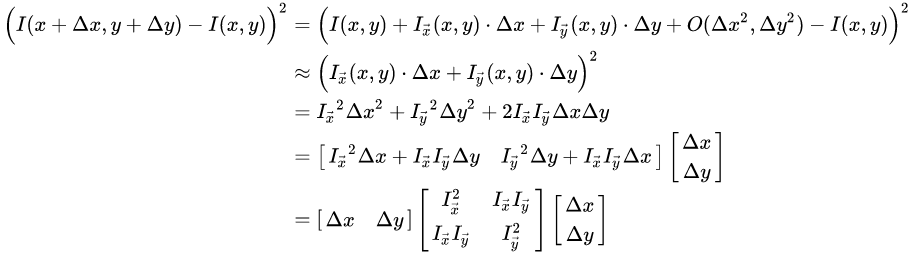
其中，
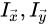分别代表I在（x, y）点两个方向上的梯度，简化了写法，代入亮度变化方程，得到
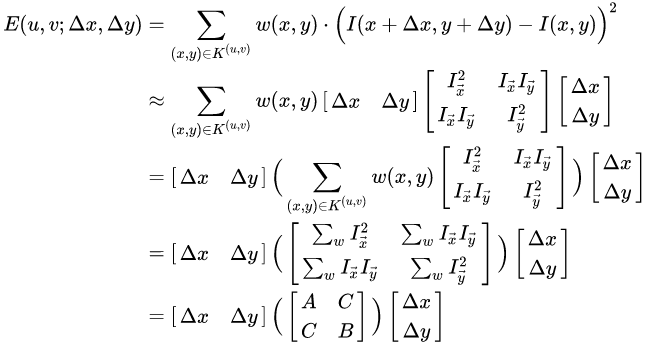
将公式展开：
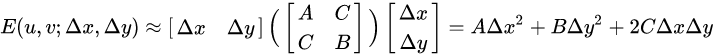
可见，是一个关于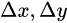
的二次函数，
对该函数取某个值Q（如1）的横切面，即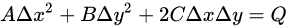
，其中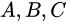
由局部窗口的两个方向梯度
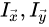决定，
不同局部窗口会得到不同的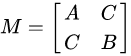
，也会得到不同的函数横切面，横切面的形状也有所不同。
当
，该函数表示椭圆（回顾椭圆性质，
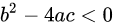），证明：
因此 在值 Q 的横切面，近似是一个椭圆。
特殊情况下，
当椭圆表达式不存在 交叉项，此时椭圆的长短轴恰好在 x, y 方向上，
，
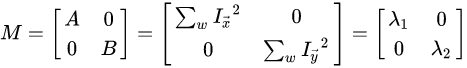决定了椭圆的形状，
此时，局部区域的梯度方向信息都集中在对角线上，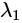
表征了 x 方向的梯度信息，
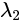表征了 y 方向的梯度信息。很简单得到以下的结论：
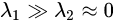，该局部窗口内主要是x方向的梯度信息，y方向没有梯度，所以是边缘；
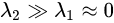，该局部窗口内主要是y方向的梯度信息，x方向没有梯度，所以是边缘；
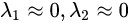，该局部窗口内，两方面的梯度信息都几乎为0，所以是平坦区域；
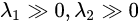，该局部窗口内，x,y方向上都由较剧烈的梯度变化，所以是角点；
但以上的特殊情况，是实际梯度恰好垂直，不垂直的话，就只能看实际梯度信息在x,y方向的分量是多少，占据越多，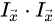
越接近于0，上述结论越靠谱。
通常情况，
考虑实际梯度垂直，但是不在x,y方向上，呈现一定的角度，此时可以通过正交变换，消除交叉项，将椭圆旋转到实际的梯度方向上，
M是实对称矩阵，可以作特征值分解，即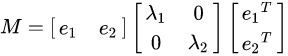
，
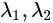是M的两个特征值，e1、e2是特征向量。
则亮度变化函数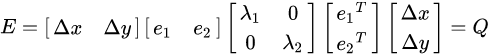
，
展开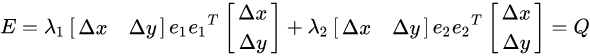
，写成椭圆的形式
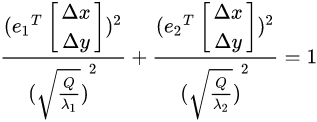
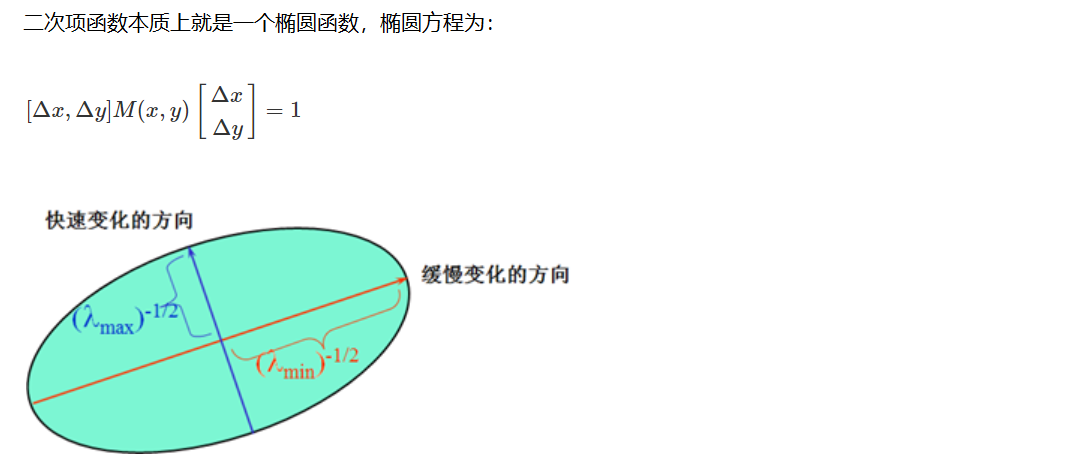
这是一个新的椭圆，长短轴由 决定，坐标轴方向由两个特征向量
决定。此时的椭圆恰好满足了上面的特殊情况，在垂直的新梯度方向上，实际梯度由
决定，依旧是那一套
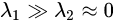- ，该局部窗口内主要是x方向的梯度信息，y方向没有梯度，所以是边缘；
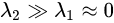- ，该局部窗口内主要是y方向的梯度信息，x方向没有梯度，所以是边缘；
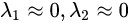- ，该局部窗口内，两方面的梯度信息都几乎为0，所以是平坦区域；
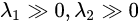- ，该局部窗口内，x,y方向上都由较剧烈的梯度变化，所以是角点；
总结：
回顾上面的过程，从 是个二次函数，到取
这个横切面是个椭圆，到椭圆长短轴在不在 x, y 方向上做了分类讨论——特殊情况，恰好在 x, y 方向上，直接判断
的特征值即可；不在 x, y 方向上，特征值分解做正交变换，将椭圆旋转到长短轴与实际梯度方向重合，这时候，是在这个新方向上的特殊情况，也是直接判断
的特征值即可。
（默认需要检测的角点两个方向的实际梯度垂直或者近似垂直）
综上，可以根据 矩阵的两个特征值
大小相对关系，判断角点。
实际运算，图像中每个点所在局部窗口都有一个对应的 矩阵，如何衡量
大小？ Harris 的作者提出了一种新方案，
角点响应值：
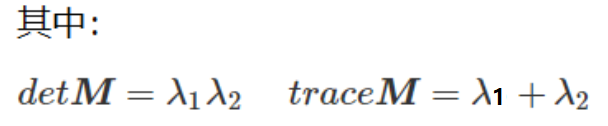
通过判断 来检测角点,
是一个很小的数，通常取值
。
如何看待角点响应值？
假设 是同一个大量级的数，设为
，则
，因为
是一个很小的数，此时的
也是一个很大的数，可以用来判断角点。
假设 是同一个小量级的数，设为
，同上
，接近于 0，可以用来判断平坦区域。
假设 一大一小，
，则
，其中
是一个极微小量，甚至如果
，该响应值还是负的，可以用来判断边缘。
步骤
1. RGB彩色图片转成灰度图；
2. 使用Sobel等梯度算子计算每一个点x,y两个方向上的梯度，如
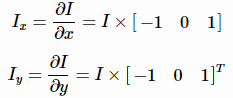
3. 计算图像两个方向梯度的乘积 和
，为构建
矩阵做准备；
4. 对 和
做局部窗口的高斯滤波（或均值滤波），计算中心点为（x, y）的局部窗口W对应的矩阵M；
5. 对图像每一个点，构建 ，求Harris响应值
，参数
一般取 0.04 - 0.06；
6. 过滤响应值，响应值大于一定阈值的点保存，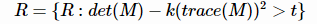
保存作为角点。
7. 每个角点，统计局部特征，做后续的图像匹配等。
