图像的空间几何变换
一 空间几何变换概念
图像几何变换又称为图像空间变换,它将一副图像中的坐标位置映射到另一幅图像中的新坐标位置。
图像的几何变换主要包括:平移、旋转、镜像、缩放、剪切、仿射、透视等。
图像的几何变换主要分为:刚性变换、相似变换、仿射变换和透视变换(投影变换)。
- 刚性变换:平移+旋转
- 相似变换:缩放+剪切
- 仿射变换:从一个二维坐标系变换到另一个二维坐标系,属于线性变换。通过已知3对坐标点可以求得变换矩阵
- 透视变换:从一个二维坐标系变换到一个三维坐标系,属于非线性变换。通过已知4对坐标点可以求得变换矩阵。
我们学习几何变换就是确定这种空间映射关系,以及映射过程中的变化参数。
图像的几何变换改变了像素的空间位置,建立一种原图像像素与变换后图像像素之间的映射关系,通过这种映射关系能够实现下面两种计算:
- 原图像任意像素计算该像素在变换后图像的坐标位置
- 变换后图像的任意像素在原图像的坐标位置
对于第一种计算,只要给出原图像上的任意像素坐标,都能通过对应的映射关系获得到该像素在变换后图像的坐标位置。将这种输入图像坐标映射到输出的过程称为“向前映射”。反过来,知道任意变换后图像上的像素坐标,计算其在原图像的像素坐标,将输出图像映射到输入的过程称为“向后映射”。但是,在使用向前映射处理几何变换时却有一些不足,通常会产生两个问题:映射不完全,映射重叠。
1. 映射不完全
输入图像的像素总数小于输出图像,这样输出图像中的一些像素找不到在原图像中的映射。
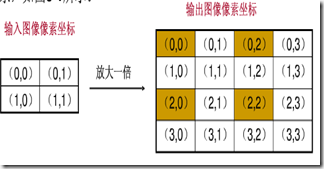
上图只有(0,0),(0,2),(2,0),(2,2)四个坐标根据映射关系在原图像中找到了相对应的像素,其余的12个坐标没有有效值。
2. 映射重叠
根据映射关系,输入图像的多个像素映射到输出图像的同一个像素上。
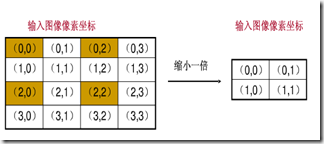
上图左上角的四个像素(0,0),(0,1),(1,0),(1,1)都会映射到输出图像的(0,0)上,那么(0,0)究竟取那个像素值呢?
要解决上述两个问题可以使用“向后映射”,使用输出图像的坐标反过来推算改坐标对应于原图像中的坐标位置。
这样,输出图像的每个像素都可以通过映射关系在原图像找到唯一对应的像素,而不会出现映射不完全和映射重叠。
所以,一般使用向后映射来处理图像的几何变换。从上面也可以看出,向前映射之所以会出现问题,主要是由于图像像素的总数发生了变化,也就是图像的大小改变了。在一些图像大小不会发生变化的变换中,向前映射还是很有效的。
二 空间几何变换
1 仿射变换
1.1 放射变换原理
仿射变换(Affine Transformation)是指在向量空间中进行一次线性变换(乘以一个矩阵)和一次平移(加上一个向量),变换到另一个向量空间的过程。
仿射变换代表的是两幅图之间的映射关系,仿射变换矩阵为2x3的矩阵,如下图中的矩阵M,其中的B起着平移的作用,而A中的对角线决定缩放,反对角线决定旋转或错切。
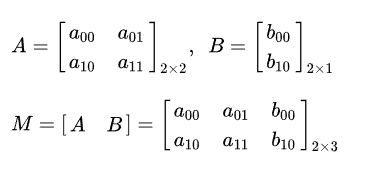
原像素点坐标(x,y),经过仿射变换后的点的坐标是T,则矩阵仿射变换基本算法原理:
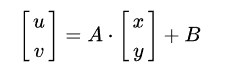
所以仿射变换是一种二维坐标(x,y)到二维坐标(u,v)之间的线性变换,其数学表达式如下:
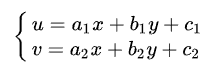
这个矩阵是2×3的,但是这会改变原始图像的维度,为此,增加一个维度,构造齐次变换矩阵3×3。
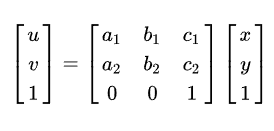
这就保持了图像的‘平直性’和‘平行性’。
平直性:直线、圆弧不变
平行性:平行关系不变,直线相对位置不变,但是夹角可能会改变。
1.2 仿射变换函数cv2.warpAffine
在OpenCV中,主要使用函数:cv2.warpAffine 来实现仿射变换。
其中cv2.warpAffine的变换矩阵为2*3矩阵。
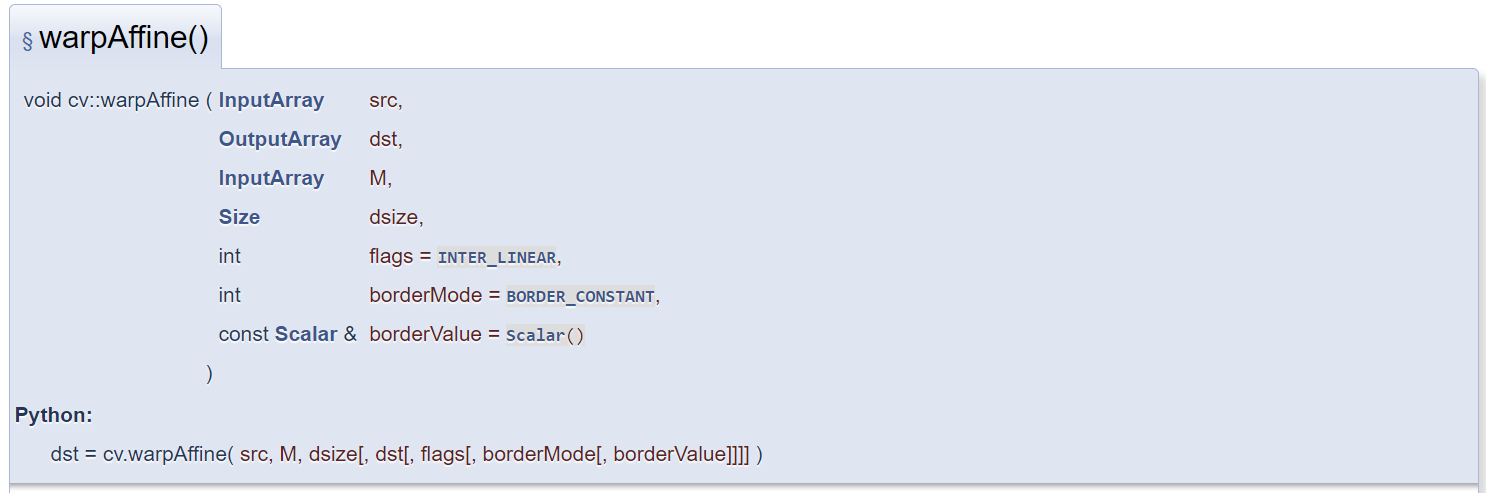
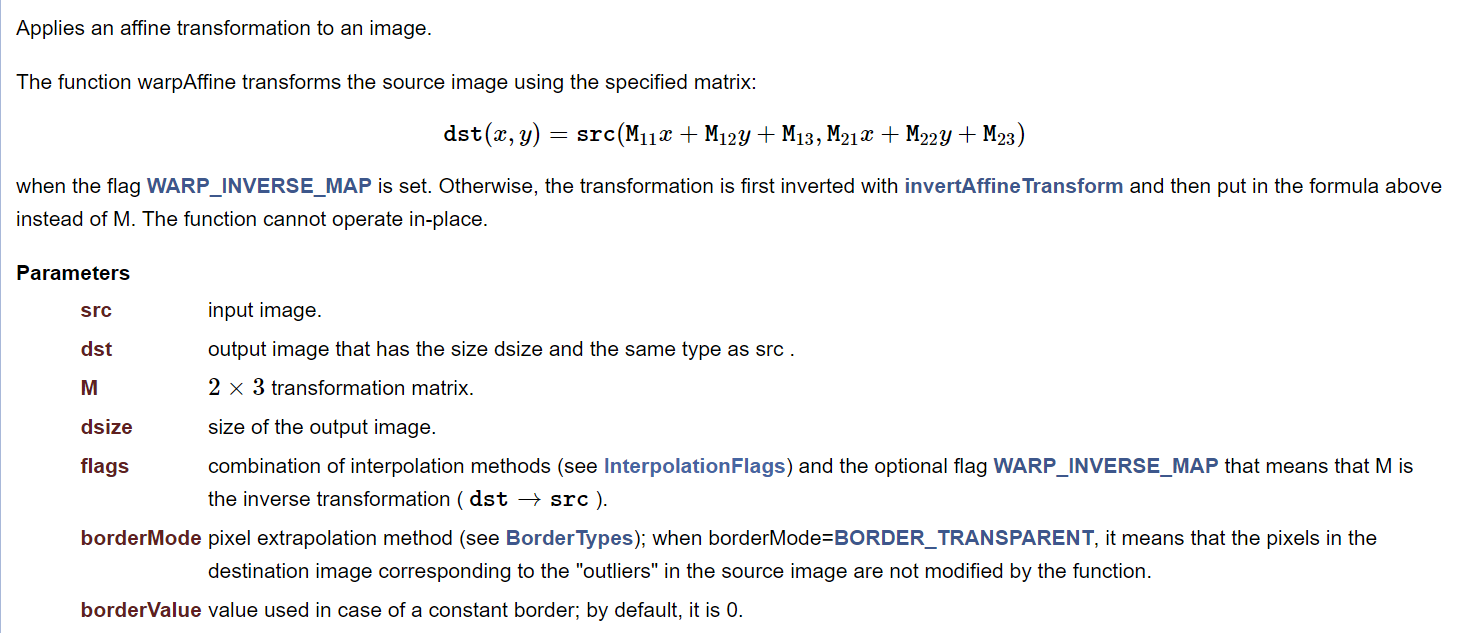
参数:
- src: 输入图像;
- M:变换矩阵;
- dsize:变换后输出图像的大小;
- flags: 插值方法的组合,int型;
- borderMode:边界像素模式;
- borderValue:边界填充值, 默认为0;
上述参数中:
M作为仿射变换矩阵,一般反映平移或旋转的关系,为InputArray类型的2×3的变换矩阵。
flages表示插值方式,默认为 flags=cv2.INTER_LINEAR,表示线性插值,
此外还有:cv2.INTER_NEAREST(最近邻插值)
cv2.INTER_AREA (区域插值)
cv2.INTER_CUBIC(三次样条插值)
cv2.INTER_LANCZOS4(Lanczos插值)
日常进行仿射变换时,在只设置前三个参数的情况下,如 cv2.warpAffine(img,M,(rows,cols))可以实现基本的仿射变换效果,但可能出现“黑边”现象。
1.3 缩放
cv.resize()
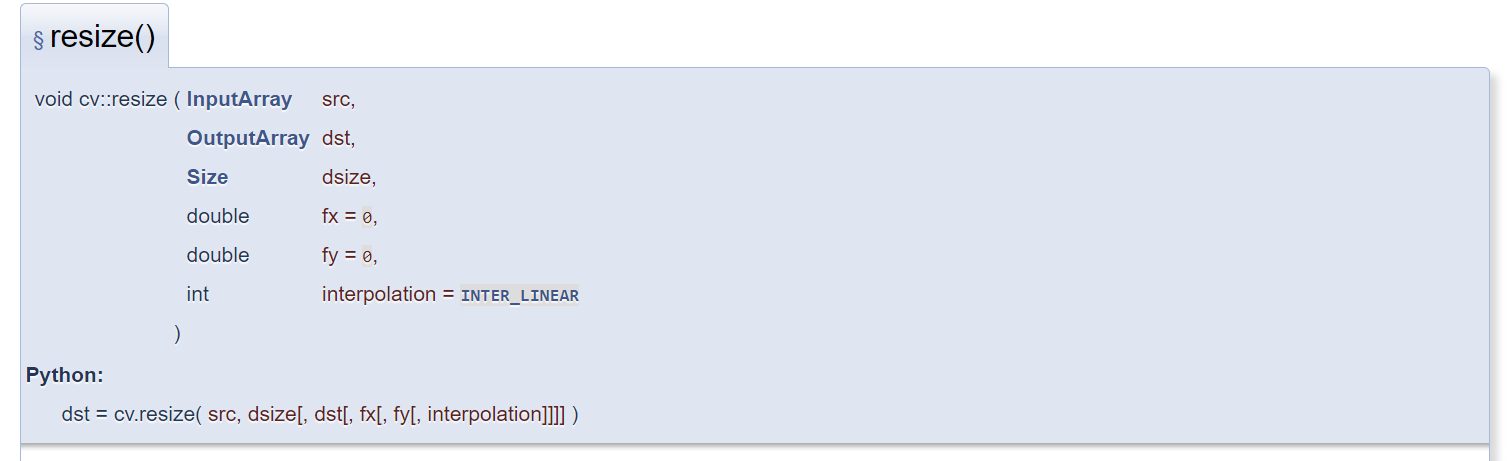

src : 原图;
dst:输出结果;
dsize: 输出图像尺寸;
fx:水平缩放比例;
fy:垂直缩放比例;
interpolation: 插值方法;
cv2.resize()实现缩放:
import cv2
import numpy as np
def cv_show(imgs):
for index, img in enumerate(imgs):
cv2.imshow("{}".format(index), img)
cv2.waitKey(0)
cv2.destroyAllWindows()
img_path = "./3color.png"
img_color = cv2.imread(img_path, cv2.IMREAD_COLOR)
img_resize1 = cv2.resize(img_color, None, fx=0.5, fy=0.5, interpolation=cv2.INTER_AREA)
height, width = img_color.shape[:2]
img_resize2 = cv2.resize(img_color, (2*width, 2*height), interpolation=cv2.INTER_CUBIC)
cv_show([img_color, img_resize1, img_resize2])
上述是缩放的两种方式,默认参数是INTER_LINEAR,缩小时使用INTER_AREA效果较好,放大时使用INTER_CUBIC(速度会慢)和INTER_LINEAR效果较好。
插值方法:
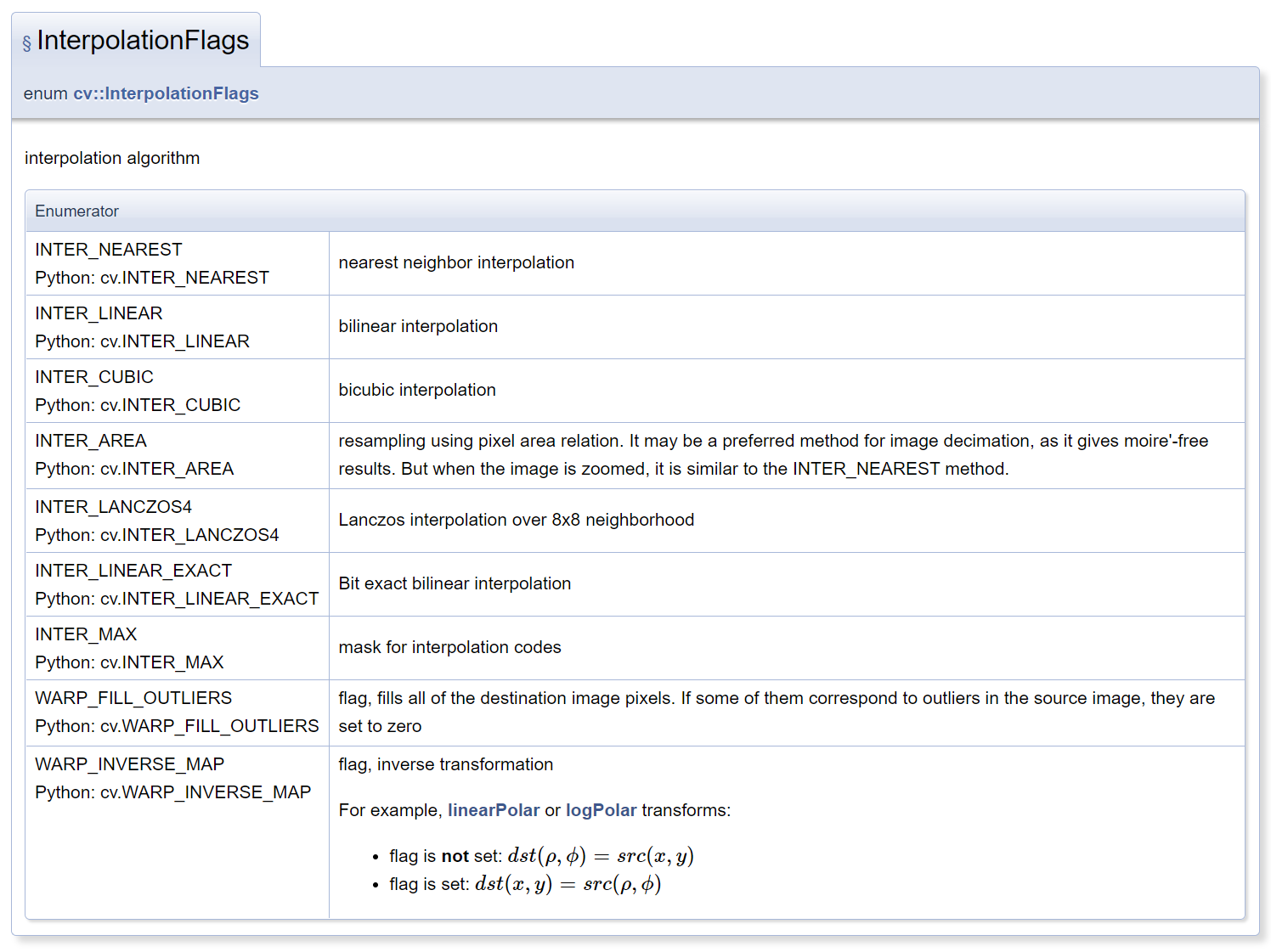
1.4 平移
图像的平移变换就是将图像所有的像素坐标分别加上指定的水平偏移量和垂直偏移量。
平移变换根据是否改变图像大小分为两种,直接丢弃或者通过加目标图像尺寸的方法使图像能够包含这些点。
1.4.1 平移变换原理
假设原来的像素的位置坐标为(x0,y0),经过平移量(△x,△y)后,坐标变为(x1,y1),如下所示:
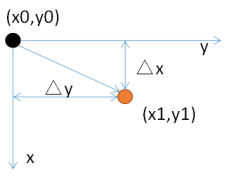
用数学式子表示可以表示为:
用矩阵表示为:
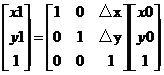
称为平移变换矩阵M(因子),△x和△y为平移量。
因此,可以通过人为定义一个平移矩阵M,实现图像平移。平移矩阵M必须是两行三列的矩阵,格式如下:
M = np.float32([[1, 0, x], [0, 1, y]])
在矩阵第一行中表示的是[1,0,x],其中x表示图像左右移动的距离,如果x是正值,则表示向右移动,如果是负值的话,则表示向左移动;
在矩阵第二行表示的是[0,1,y],其中y表示图像上下移动的距离,如果y是正值的话,则向下移动,如果是负值的话,则向上移动。
1.4.2 平移变换实现
平移变换例子:
import cv2 import numpy as np def cv_show(imgs): for index, img in enumerate(imgs): cv2.imshow("{}".format(index), img) cv2.waitKey(0) cv2.destroyAllWindows() img_path = "./girl.png" img_color = cv2.imread(img_path, cv2.IMREAD_COLOR) # 2*3矩阵, x_new = 1*x + 0*y + bias_x, y_new = 0*x + 1*y + bias_y bias_x = 20 # 向右移动20 bias_y = 50 # 向下移动50 M = np.float32([[1,0,bias_x],[0,1,bias_y]]) dst1 = cv2.warpAffine(img_color, M, (img_color.shape[1], img_color.shape[0])) cv_show([img_color, dst1])

1.5 旋转
1.5.1 旋转矩阵cv2.getRotationMatrix2D
图片旋转需要确定旋转角度,可以通过编写一个旋转函数,再进行仿射变换即可实现图片旋转。
构造旋转矩阵函数cv2.getRotationMatrix2D():
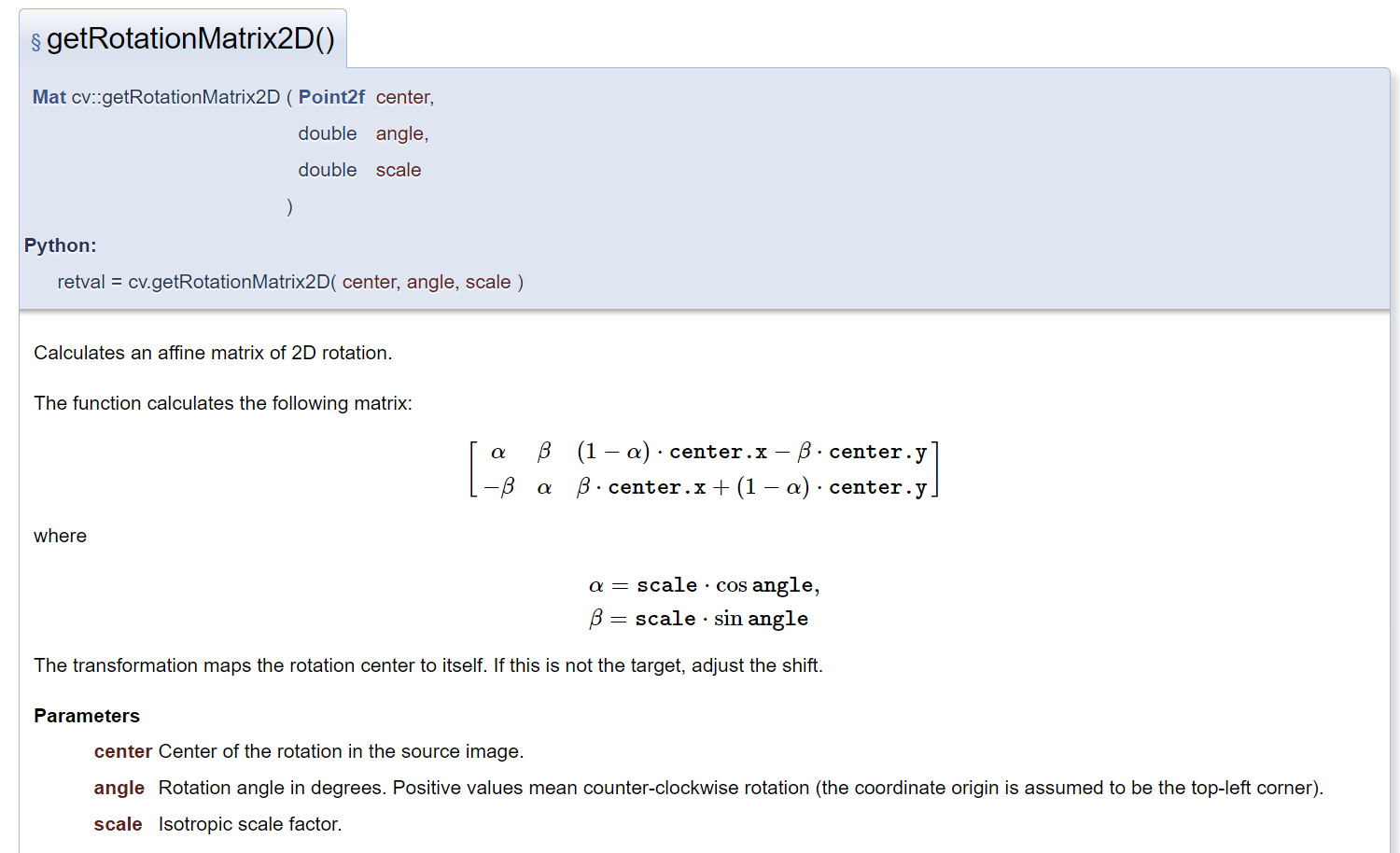
参数:
- Point2f center:表示旋转的中心点;
- double angle:表示旋转的角度, 正数表示逆时针旋转,负数表示顺时针旋转;
- double scale:图像缩放因子,大于1表示扩大,小于1表示缩小,1表示维持大小不变;
# 构造旋转矩阵, 以图像中心点为旋转中心, 40表示旋转40°, 1表示不缩放; M = cv2.getRotationMatrix2D(((cols-1)/2.0, (rows-1)/2.0),40,1)
1.5.2 代码实现
import cv2
import numpy as np
def cv_show(imgs):
for index, img in enumerate(imgs):
cv2.imshow("{}".format(index), img)
cv2.waitKey(0)
cv2.destroyAllWindows()
img_path = "./girl.png"
img_color = cv2.imread(img_path, cv2.IMREAD_COLOR)
rows, cols = img_color.shape[:2]
# 构造旋转矩阵, 以图像中心点为旋转中心, 40表示旋转40°, 1表示不缩放; M = cv2.getRotationMatrix2D(((cols-1)/2.0, (rows-1)/2.0),40,1)
# 旋转变换 dst = cv2.warpAffine(img_color,M, (cols, rows)) cv_show([img_color, dst])
先通过设定的角度、中心获取旋转矩阵,然后再做图像变换,正角度逆时针旋转图像,负角度顺时针旋转图像。

1.6 镜像变换
1.6.1 镜像变换原理
图像的镜像变换分为两种:水平镜像和垂直镜像。水平镜像以图像垂直中线为轴,将图像的像素进行对换,也就是将图像的左半部和右半部对调。垂直镜像则是以图像的水平中线为轴,将图像的上半部分和下班部分对调。
水平变换:
向前映射其逆变换为:
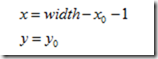
向后映射:
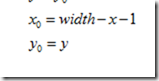
2.垂直镜像变换

其逆变换为
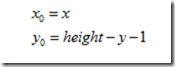
4 仿射变换
这里有两种方式:
方式一:warpAffine,输入图像选取3个点,输出图像选取3个点,使之一一对应,这样就有了对应关系,然后用cv2.getAffineTransform获取转换矩阵,再进行变换。
方式二:warpPerspective,输入图像选取3个点,输出图像选取3个点,使之一一对应,注意这里输入图像的4个点至少有3个点是不在一条直线的,然后用cv2.getPerspectiveTransform获取转换矩阵,再进行变换。
import cv2
import numpy as np
def cv_show(imgs):
for index, img in enumerate(imgs):
cv2.imshow("{}".format(index), img)
cv2.waitKey(0)
cv2.destroyAllWindows()
img_path = "./girl.png"
img_color = cv2.imread(img_path, cv2.IMREAD_COLOR)
rows, cols = img_color.shape[:2]
# warpAffine方式
if 1:
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])
M = cv2.getAffineTransform(pts1, pts2)
dst1 = cv2.warpAffine(img_color, M, (cols, rows))
# warpPerspective方式
if 1:
pts1 = np.float32([[50,50],[200,50],[50,200], [200, 200]])
pts2 = np.float32([[10,100],[200,50],[100,250], [300,200]])
M = cv2.getPerspectiveTransform(pts1, pts2)
dst2 = cv2.warpPerspective(img_color, M, (cols, rows))
cv_show([img_color, dst1, dst2])





