Live2D

sx组作业小结

  • 就做了几道题还要写……
  • 我就按照我想题看TJ的顺序写了。

CF573 E. Bear and Bowling

Problem

  • https://codeforces.com/contest/573/problem/E
  • 给你一个长度为\(n(≤10^5)\)的数列\(\{a_n\}(|a_i|≤10^7)\)。可以删任意项。设最后删剩\(k\)个数\(s_1,s_2,...,s_k\)，求\(\sum_{i=1}^k i*s_i\)的最大值。

Solution

  • 结论题。
  • 考虑一种弱智DP：设\(f_{i,j}\)表示前i个数，留j个数的最大值，那么显然有转移：\(f_{i,j}=max(f_{i-1,j},f_{i-1,j-1}+j*a_i)\)。
  • 但是实际上有一个结论：每次从\(f_{i-1}\)转移到\(f_i\)时，必有一个分界点k，使得\(\forall j≤k\)的都是直接从\(f_{i-1,j}\)转移过来，\(\forall j>k\)都是从\(f_{i-1,j-1}+j*a_i\)转移。这里有一个证明：https://www.luogu.com.cn/blog/Mrsrz/solution-cf573e
  • 其实还有一个更强的结论：把位置i的贡献记作\(k_i*a_i+b_i\)，其中\(k_i\)为i前已被选的数个数+1，\(b_i\)为i后已被选的数总和；那么每次贪心选贡献最大的位置一定最优。这里有证明：https://www.cnblogs.com/heyujun/p/11766283.html 用这个结论可以很简单地推出上一个结论。
  • 知道这些结论之后，不必打\(O(n^{1.5})\)的分块维护凸壳；我们可以直接维护一颗平衡树，每次在平衡树上二分出那个分界点k，前面不变，中间插一个点，后面加一个等差数列。实现时可以差分，这样就变成区间加一个数；然后单点查询就变成求前缀和。

Code

CF506 E. Mr. Kitayuta's Gift

Problem

Solution

  • 经典老题。好像听人讲过，可惜我依然看了TJ才会。
  • 考虑一种不会算重的DP方式。我们从内往外构造字符串，每次添加两个字符，若新添字符与当前s两端（或一端）相同，则匹配成功，继续匹配更外层的字符。官方TJ有张图：
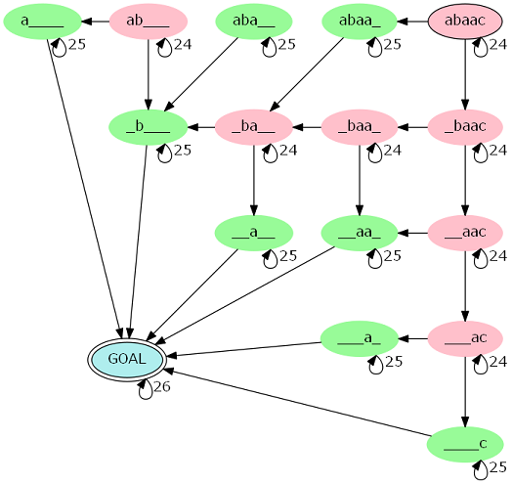
  • 红点两边字符不同，绿点则相同。
  • 我们发现一条链上有i个红点，就有\(\lceil\frac{|s|-i}2 \rceil\)个绿点。同时我们转移时，并不关心红绿点的顺序，而只关心经过的个数；于是可以提前用一个\(O(|s|^3)\)DP出红点个数为i的方案数，然后把方案数记在红点连绿点的边上即可。图可以继续压缩，这里盗一张CQzhangyu的图：
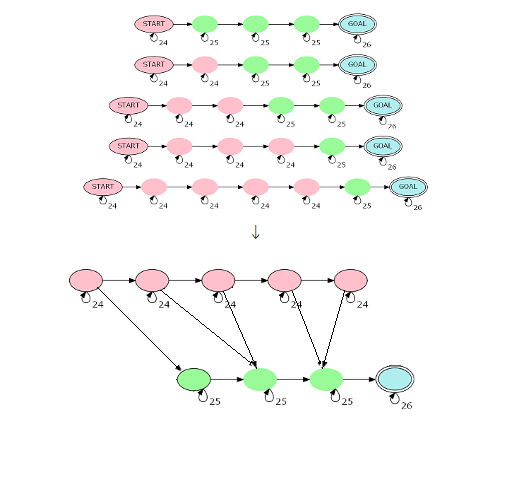
  • 然后就是喜闻乐见的矩乘优化。\(n+|s|\)为奇数要额外做一遍矩乘，减去算多的贡献（就是形如[i,i+1]的绿点不能在最后一步转移到终点，因为最后一步只能带走一个字符）。实际的建图有些怪，要好好考虑。

Code

AGC020 D - Min Max Repetition

Problem

  • https://atcoder.jp/contests/agc020/tasks/agc020_d
  • 给出\(Q(≤10^3)\)组询问，形如\(A,B,C,D(1≤A,B≤5*10^8,D-C+1≤100)\)，求一个由A个'A'、B个'B'构成，最长连续段最短，然后字典序尽量小的串，输出其C~D位。

Solution

  • 水题。
  • 最长连续段长度显然是\(k=\lfloor\frac{A+B}{\min(A,B)+1}\rfloor\)。然后有一个最优策略：前面是k个A+1个B的循环，后面是k个B+1个A的循环（但后面不一定是k个B开头）。二分出前面一段的最长长度即可。

Code

ARC098 F - Donation

Problem

  • https://atcoder.jp/contests/arc098/tasks/arc098_d
  • 给定一个N个点、M条边\((1≤N,M≤10^5)\)的简单无向图，每个点有A、B\((1≤A,B≤10^9)\)两种点权。接下来要玩游戏：
  • 先带着W元钱，选定一个点s站上去，要求\(A_s≤W\)。接下来可以移动到一个相邻的点v满足\(A_v≤W\)；也可以给当前点捐款，捐B元，要求捐后\(W≥0\)。每个点都要捐，求一开始至少需多少钱。

Solution

  • 首先，如果把经过的节点依次记下来，那么对一个点捐钱的时机一定是最后经过该点的时候。那么在任意时刻，还未捐钱的点一定是一个连通块。然后，看到数据范围，即可猜测这是一道排序题。
  • 有个神必转化：\(W≥A\land W-B≥0\Rightarrow W-B≥\max(A-B,0)\)。设\(C_i=\max(A_i-B_i,0)\)，则若有一个捐钱顺序排列p，\(p_k\)对W的限制即为：\(W≥\sum_{i=1}^k B_{p_i} +C_{p_k}\)。
  • 考虑当前未捐钱的点，设这里面C最大的为x，那么将x删去后会分裂成若干个连通块，设它们分别为\(G_1,G_2,G_3,...,G_k\)。有个结论：我们按照\(G,G,...,x,G\)的顺序捐钱一定不劣（即一定可以让某个G完全在x之后选）。设那个垫底的块为\(G_q\)，假如\(G_q\)中有1个点先于x被捐，设其为y，我们发现先x后y的代价为\(\max(B_x+C_x,B_x+B_y+C_y)\)，先y后x的代价为\(\max(B_y+C_y,B_x+B_y+C_x)\)。
  • 据此可设计一种贪心做法：按C从小到大依次激活每个点，每次激活x时，让所有已被激活了的、在原图中与x有边的y所在的树根父亲连向x，然后计算x的子树的答案。

Code

AGC020 E - Encoding Subsets

Problem

Solution

  • 这就是个暴力题。
  • 设F(S)表示串S的答案，G(S)表示串S的不可分割的答案（即外层有一对括号，或者|S|=1），记忆化算一下。具体地说，算F(S)就枚举S的一个非零前缀P，统计\(\sum G(P)*F(S-P)\)；算G(S)就枚举一个串长的约数\(d\)，把S分成\(\frac {|S|}d\)段，每一段按位与起来得到一个长为\(d\)的串T，统计\(\sum F(T)\)。
  • 可以感受到状态数很少。\(l\)比较小时，长度\(≤l\)的串个数为\(2^{l+1}-1\)；\(l\)比较大时，长度\(≥l\)的串也不多，因为它只能是某几段按位与、取前缀、按位与这样反复，很容易变成全零。

Code

AGC036 D - Negative Cycle

Problem

Solution

  • 597发明了一种DP做法：https://blog.csdn.net/a1847225889/article/details/108673136
  • 可惜他的空间要\(O(n^3)\)，比正解劣。
  • 这题可以把它看成差分约束系统。假设点从1开始编号，设\(d_i\)表示1到i的最短路，图的性质保证了\(d_i≥d_{i+1}\land d_i-1≤d_{i+1}\)，无负环相当于有解。
  • 可以设\(f_{i,j}\)表示\(d=d_i\)的点恰为\([i,j]\)，且\([1,j]\)无负环的最小花费。每次从\(f_{i,j}\)转移到\(f_{j+1,k}\)。

Code

posted @ 2020-09-21 22:42  Iking123  阅读(164)  评论(0)  编辑  收藏  举报