splay(伸展树)&LCT(动态树)复杂度略证
Preface
- 貌似n年前就听学长讲过,可惜当时太菜,什么都听不懂……
- 最近
太闲于是稍微学习了一下。在此做个小结。
一些约定/定义
- 点\(i\)的子树大小表示为\(size(i)\)。
- 点\(i\)的势函数\(R(i)=\lceil\log_2size(i)\rceil\)。注意这里有一个美妙的上取整。
- 全局势函数\(\Phi=\sum_i R(i)\)。
- \(\Phi(t)\)表示时刻\(t\)的\(\Phi\),即进行\(t\)次伸展操作后的\(\Phi\)。显然对于任意\(t\in N\),都有\(\Phi(t)\in[n,n\log_2n]\)。
splay
- 只需分析伸展操作的复杂度。
分析
- 回顾一下rotate:若父亲是根,单旋一次;否则,若父亲和祖父方向一致,先旋父亲再旋自己;否则旋两次自己。因此我们只需分析zig、zig-zig、zig-zag。
- 博主太懒了,盗几张图吧……
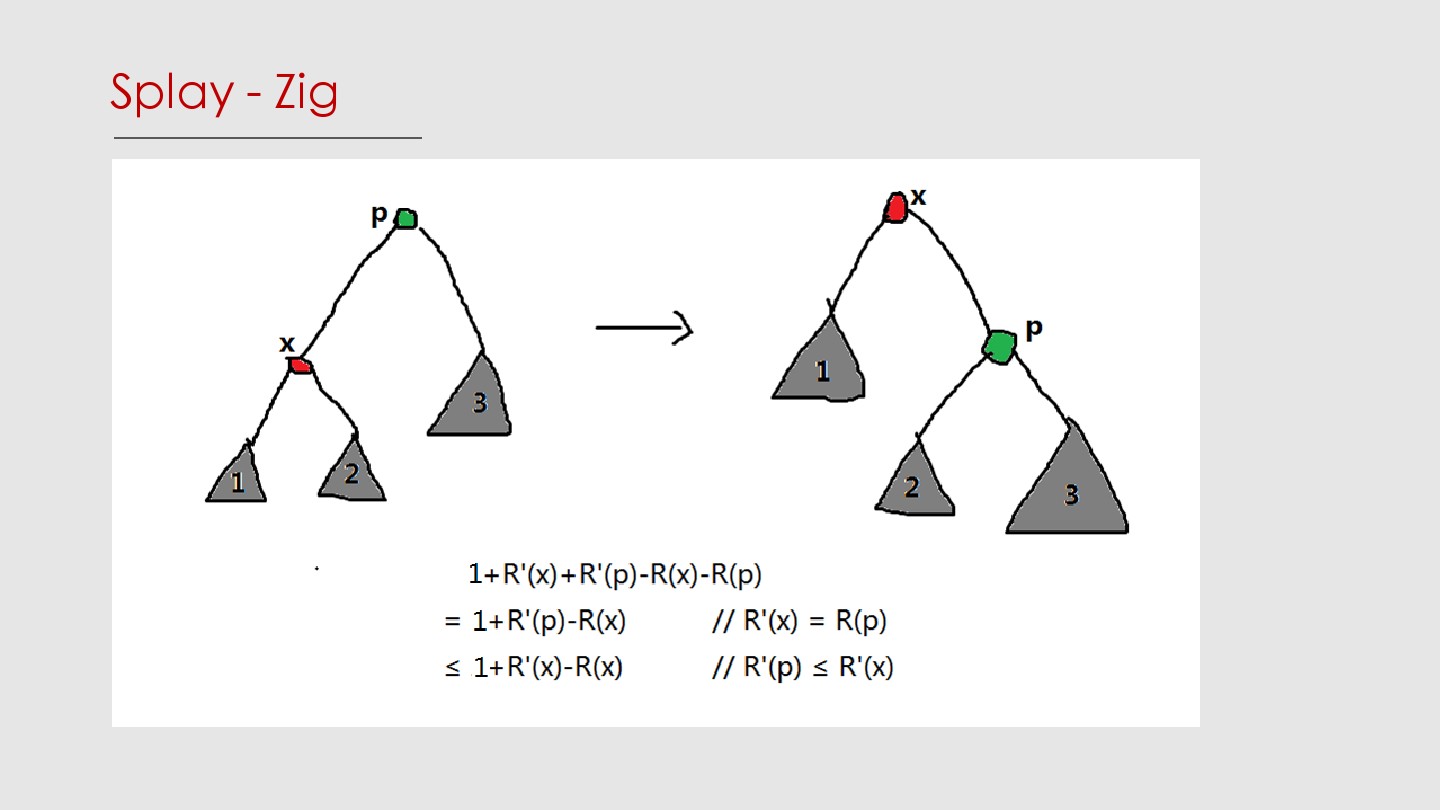
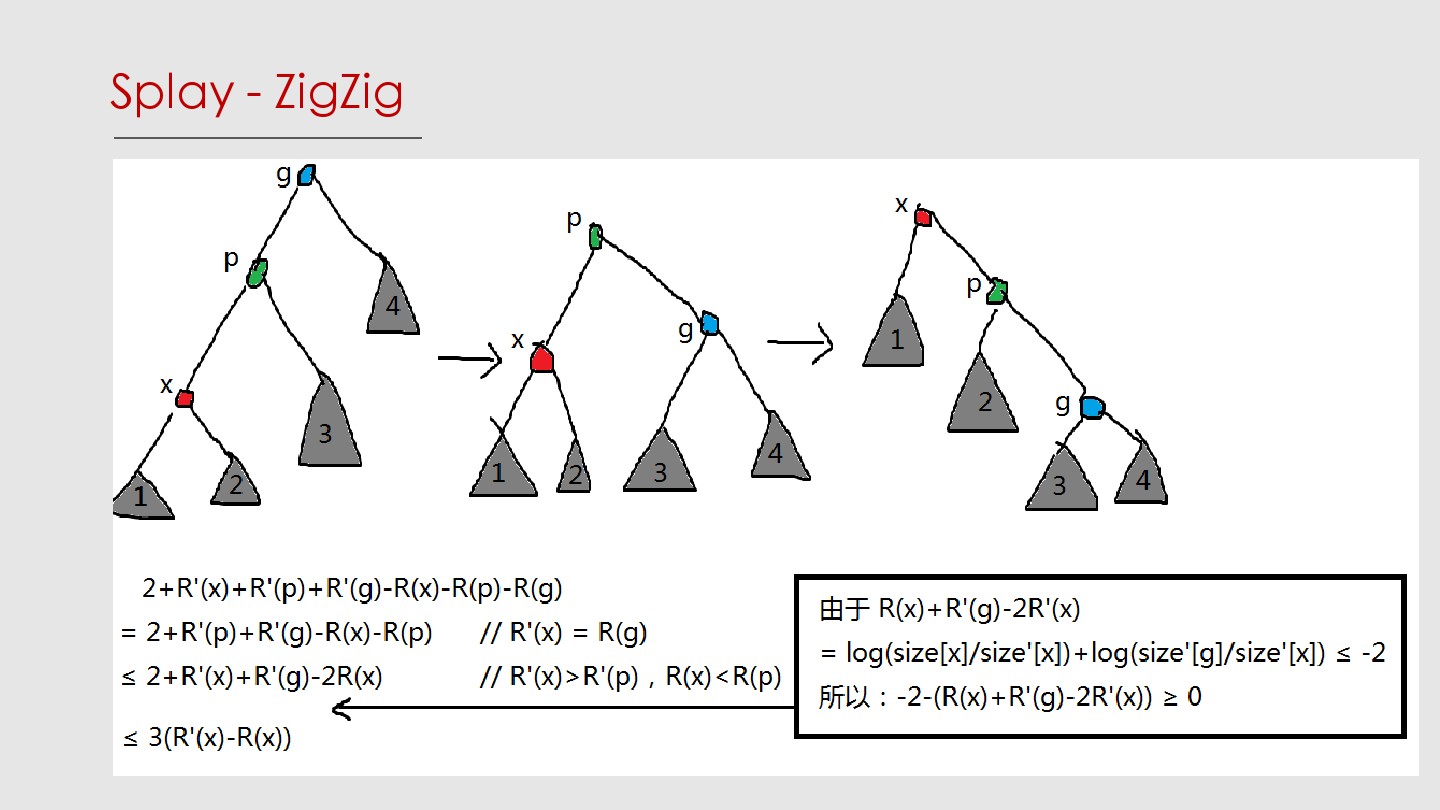
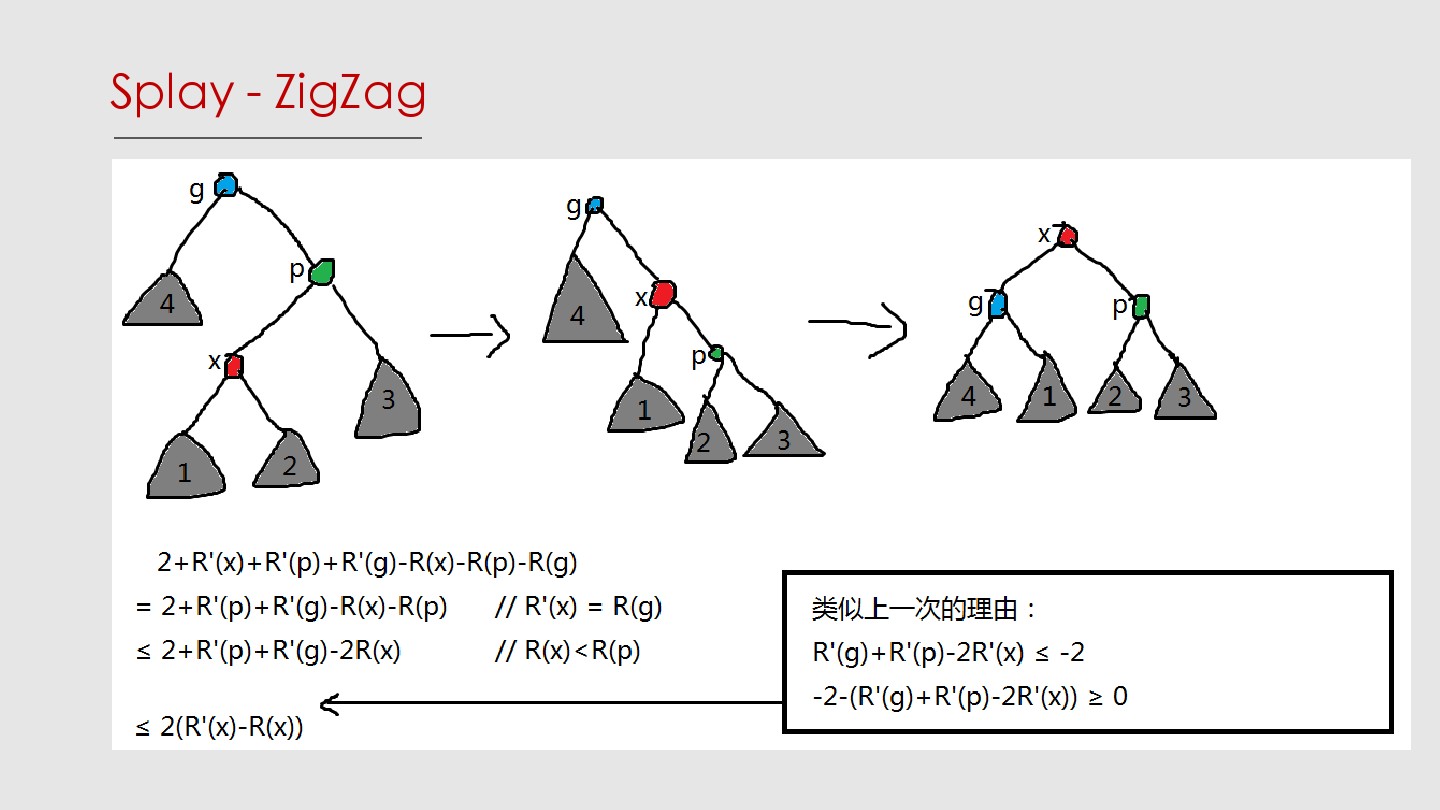
- 注意,这里面写的\(1+R'(x)-R(x)\)什么的实际上是全局势函数的变化量与新增耗时的总和,即\(\Delta\Phi+\Delta T\)。这大概是我以前没听懂的主要原因吧……
- 把zig-zag的代价也放缩成\(≤3(R'(x)-R(x))\)。那么如果我们把一个点\(v\)伸展到根,总代价\(W≤1+3(R(root)-R(v))=O(\log n)\)。换句话说,一次伸展操作会使全局势函数与耗时的总和变化\(W\),并且这个\(W\)是\(O(\log n)\)的。
- 那么如果我们对一棵大小为\(n\)的splay做\(m\)次伸展操作,其均摊复杂度\(T=\sum W-\Phi(m)+\Phi(0)=O((n+m)\log n)\)。
- 这时我们就不得不佩服Daniel Sleator和Robert Endre Tarjan的脑子,居然能想到这种神奇的双旋方式,将\(\Delta T=1\)美妙地混入\(R'(x)-R(x)\)当中;而且我们可以发现,如果不这样旋,无法把\(1\)给合并进去。这也是胡乱旋会T飞的理由。
LCT
- 只需分析access操作的复杂度。
分析
- access的复杂度来源于两部分:1.在splay中走的复杂度;2.虚实变换的复杂度。
- 在splay中走的复杂度可以参考上文的证法,它的均摊复杂度也是\(O((n+m)\log n)\)的。(\(n\)个点的LCT,进行\(m\)次access操作)
- 接下来考虑虚实变换。
- 参照重链剖分,我们定义从\(u\)连向满足\(size(v)≥\frac{size(u)}2\)的\(v\)的虚边为重虚边,\(size(v)<\frac{size(u)}2\)的为轻虚边。
- 定义势能函数\(p\)表示LCT中重虚边的数量。和链剖一样,每次最多走\(\log_2 n\)条轻虚边,也就至多使\(p+=\log_2 n\),这部分最坏情况下花\(O(\log n)\)的时间使\(p\)增加\(\log_2 n\);而每访问一条重虚边,我们就要花\(O(1)\)的时间使\(p--\),并且此时不会有新的重虚边产生。
- 因此虚实变换的均摊复杂度是\(O(n+m\log n)\)。
- 综上,LCT的均摊复杂度为\(T=O((n+m)\log n)\)。
参考文献
怎么感觉“文献”这个词莫名喜感……- Splay和LCT的复杂度分析
- 均摊分析简介


