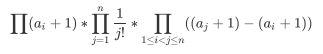JZOJ6776【NOI2020模拟7.31】T2 path（LGV引理+范德蒙德行列式）

Description

• 有\(n\)个人，第\(i\)个人一开始在\((0,a_i)\)，最后要走到\((i,0)\)，每次只能从\((i,j)\)走到\((i+1,j)\)或者\((i,j-1)\)。
• 求使得路径两两不相交的方案数，对\(998244353\)取模。经过同一点算相交。
• \(a_i≤a_{i+1},n≤5*10^5,0≤a_i<10^6\)。

Solution

• 假设只有两个人，我们交换他们的终点，他们的路径必然相交；可以发现交换终点后的方案包含了所有相交方案。
• 当\(n>2\)时，发现这就是一个容斥的问题。设排列\(\sigma\)的方案数为\(\omega(\sigma)\)，其逆序对数为\(N(\sigma)\)，答案应该是\(\sum_{\sigma} (-1)^{N(\sigma)}\omega(\sigma)\)。
• 实际上有一个叫LGV引理的东西。这篇专栏里有一点介绍：https://zhuanlan.zhihu.com/p/64482425。
• 然后OI Wiki上的例题就是本题的弱化版……

---

• 根据LGV引理，我们要求\(A_{i,j}=C_{a_i+j}^j\)的行列式。每一列将\(\frac 1{j!}\)提出来，就变成\((a_i+1)^\overline j\)。随便归纳可知，我们可以通过初等变换把它消成\((a_i+1)^j\)。
• 范德蒙德行列式：一个方阵\(A\)中的每一列都是以\(x_i\)为公比的等比数列，则\(\det A=\prod_{i>j}(x_i-x_j)\)。这个也可以随便归纳证明。
• 本题最后的式子就变成了：
  
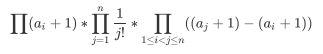
• 后面的那个东西要卷积。具体地说，我们把\(\sum x^{a_i}\)和\(\sum x^{-a_i}\)卷起来，结果中\([x^k]\)的意义即是差为\(k\)的次数，然后用个快速幂乘起来。由于这是指数，正常来说应该对\(998244352\)取模；但如果起点相同我们可以直接判掉，这样\(a_i\)就两两不同，一个差的出现次数最多只有\(n/2\)。
• 时间复杂度\(O(n\log n)\)。

Code

#include<cstdio>
#include<algorithm>
#define P(x,y) x=(x+y)%mo
#define T(x,y) x=x*(y)%mo
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define go(i,a,b) for(int i=a;i< b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
typedef long long ll;
const ll mo=998244353;
ll fpow(ll x,ll y) {ll a=1; for(;y;y/=2,T(x,x))if(y&1)T(a,x); return a;}
namespace NTT
{
	const int NM=1<<22;
	int tf[NM]; ll w[NM];
	void build(int n)
	{
		for(int i=1;i<n;i*=2)
		{
			w[i]=1; ll v=fpow(3,(mo-1)/2/i);
			go(j,1,i) w[i+j]=w[i+j-1]*v%mo;
		}
	}
	void DFT(ll a[NM],int n,bool f)
	{
		go(i,1,n)
		{
			tf[i]=tf[i/2]/2+(i&1)*(n/2);
			if(i<tf[i]) swap(a[i],a[tf[i]]);
		}
		ll v;
		for(int i=1;i<n;i*=2) for(int j=0;j<n;j+=2*i) go(k,0,i)
			v=a[i+j+k]*w[i+k]%mo, a[i+j+k]=(a[j+k]-v+mo)%mo, P(a[j+k],v);
		if(f)
		{
			reverse(a+1,a+n);
			v=fpow(n,mo-2);
			go(i,0,n) T(a[i],v);
		}
	}
	void mtp(ll a[NM],ll b[NM],int n1)
	{
		DFT(a,n1,0); DFT(b,n1,0);
		go(i,0,n1) T(a[i],b[i]);
		DFT(a,n1,1);
	}
}
using namespace NTT;
const int N=1<<22,M=1e6;
int n;
ll x,la,fac[N]={1},a[N],b[N],ans=1;
int main()
{
	freopen("path.in","r",stdin);
	freopen("path.out","w",stdout);
	scanf("%d",&n);
	fo(i,1,n)
	{
		scanf("%lld",&x), a[x]++, b[M-x]++, T(ans,x+1), fac[i]=fac[i-1]*i%mo;
		if(i>1&&x==la) {puts("0"); return 0;}
		la=x;
	}
	x=fpow(fac[n],mo-2);
	fd(i,n,1) T(ans,x), T(x,i);
	build(N/2);
	mtp(a,b,N/2);
	fo(i,M+1,M*2) if(a[i]) T(ans,fpow((i-M+mo)%mo,a[i]));
	printf("%lld",ans);
}