P7177 MRAVI 题解

\(\Large \text{题目链接}\)

题目大意

整棵树的每条边都有流量的分配比率，部分边有“特殊性质”——将流经这条边的液体的流量平方。

现在给出每个叶子节点最终至少要流入的流量，求根节点至少要流出的流量是多少。

思路

为了叙述方便，下面将某个节点最少需要的 流量 称为该节点的“权值”。

首先我想到了一个类似于 解决普通数学问题 的做法：

将 答案，即 根节点的权值，设为 \(x\)，然后按照数据给出的要求，向叶子节点方向 一步一步进行 运算，最终得到每个叶子节点的用 \(x\) 表示的权值，但我们 只关心每个叶子节点的，题目中又给出了每个叶子节点的应有的权值，那么综合上述两个条件就可以 解方程（当然只取正数解）。下一步是从叶子节点向上 回溯 至根，将解得的结果与其 兄弟 进行比较，其父节点的权值取其所有子节点的权值中的 最大值，一直这样操作到根节点。那么得到的根节点的权值就是最终的答案。

用此方法模拟一下样例 \(2\)：

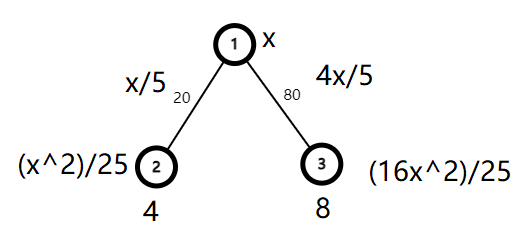
那么就可以得到两个方程：

\[\frac {x^2}{25} \geqslant 4 \]

\[\frac{16x^2}{25} \geqslant 8 \]

第一个方程解得 \(x \geqslant 10\)，第二个方程解得 \(x \geqslant \sqrt {12.5}\)。

取这两个节点的权值中最大的成为 \(1\) 号节点的权值，即 \(x=10\)，所以答案就为 \(10.00000\)。

但是上述方法的弊端也很明显，那就是不能轻松地带着 \(x\) 的一堆 系数 和 几次幂 的信息“到处走”。

感觉后半部分从叶子节点向上 回溯同时进行统计 这个过程是没问题的，可以通过 DFS 来实现，那接下来考虑怎么得到叶子节点的 权值。

其实很简单，因为数据已经给出来了，所以直接进行 DFS，如果搜到叶子节点就可以通过 简单的处理 直接得到该节点的权值：

如果连接叶子节点及其父节点的边有“特殊性质”的话，那么就将输入数据中给出的权值开方，否则就不变。

最后带这个信息，按照上面叙述的步骤，向根节点回溯即可。

实现

从根节点向下 DFS，如果搜到了 叶子节点，就处理该点权值，并返回给父节点，否则继续向下搜索。

回溯时，将一个节点 向其每一个子节点搜索的返回值 取 最大值 后返回。

细节：

1. 题目中说了 \(1\) 号点是根节点，但是不知道 \(1\) 号点的子节点都有哪些，无法开启搜索，所以钦定 \(0\) 号点为 \(1\) 号点的根节点，并由此开始搜索。

2. 过程中有关计算的变量都定义为 double 类型，最后输出时保留到小数点后 \(5\) 位（一般比题目要求多两位，这样做即可保证精度）。

\(\Large Code\)

#include <bits/stdc++.h>
using namespace std;

int read() {
	int x = 0, w = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ '0');
		ch = getchar(); 
	}
	return x * w;
}

void write(int x) {
	if (x < 0) {
		x = -x;
		putchar('-');
	}
	if (x > 9) write(x / 10);
	putchar(x % 10 ^ '0');
}

const int N = 1010;

int n;
int h[N], tot;
double w[N]; // 输入的每个点的权值

struct edge {
	int to, nxt, x, t; // x，t 的含义与题目中的相同
} e[N << 1];

void add(int u, int v, int x, int t) {
	e[ ++ tot] = (edge) {v, h[u], x, t};
	h[u] = tot;
}

double dfs(int u, int fa, int x, int t) {
	if (w[u] != -1) { // 如果搜到的点的权值不是 -1，说明这个点是叶子节点
		if (t) w[u] = sqrt(w[u] * 1.0); // 如果连接这个叶子节点的边有“特殊性质”，就开方
		return w[u] * 1.0 / (x * 1.0 / 100); // 将该点的权值除以分配到的比率，返回
	}
	double res = -1; // 为取最大值做准备
	for (int i = h[u]; i; i = e[i].nxt) {
		int j = e[i].to;
		if (j == fa) continue; // 如果又遍历到其父节点，就跳过，否则会陷入死循环
		res = max(res, dfs(j, u, e[i].x, e[i].t)); // 对这个点的所有儿子的返回值取最大值
	}
	if (t) res = sqrt(res * 1.0); // 如果连接当前点与其父节点的边有“特殊性质”，就开方
	return res * 1.0 / (x * 1.0 / 100); // 类比于叶子节点，将该点的权值除以分配到的比率
}

int main() {
	n = read();
	add(0, 1, 100, 0), add(1, 0, 100, 0); // 加两条 1 号点和 0 号点之间的边（双向边）
	for (int i = 1; i < n; i ++ ) {
		int u = read(), v = read(), x = read(), t = read();
		add(u, v, x, t), add(v, u, x, t);
	}
	for (int i = 1; i <= n; i ++ ) w[i] = read();
	printf("%.5lf\n", dfs(1, 0, 100, 0)); // 直接输出搜索的结果
	return 0;
}