2021 CSP-S 初赛题解
第 4 题
贺了张图。
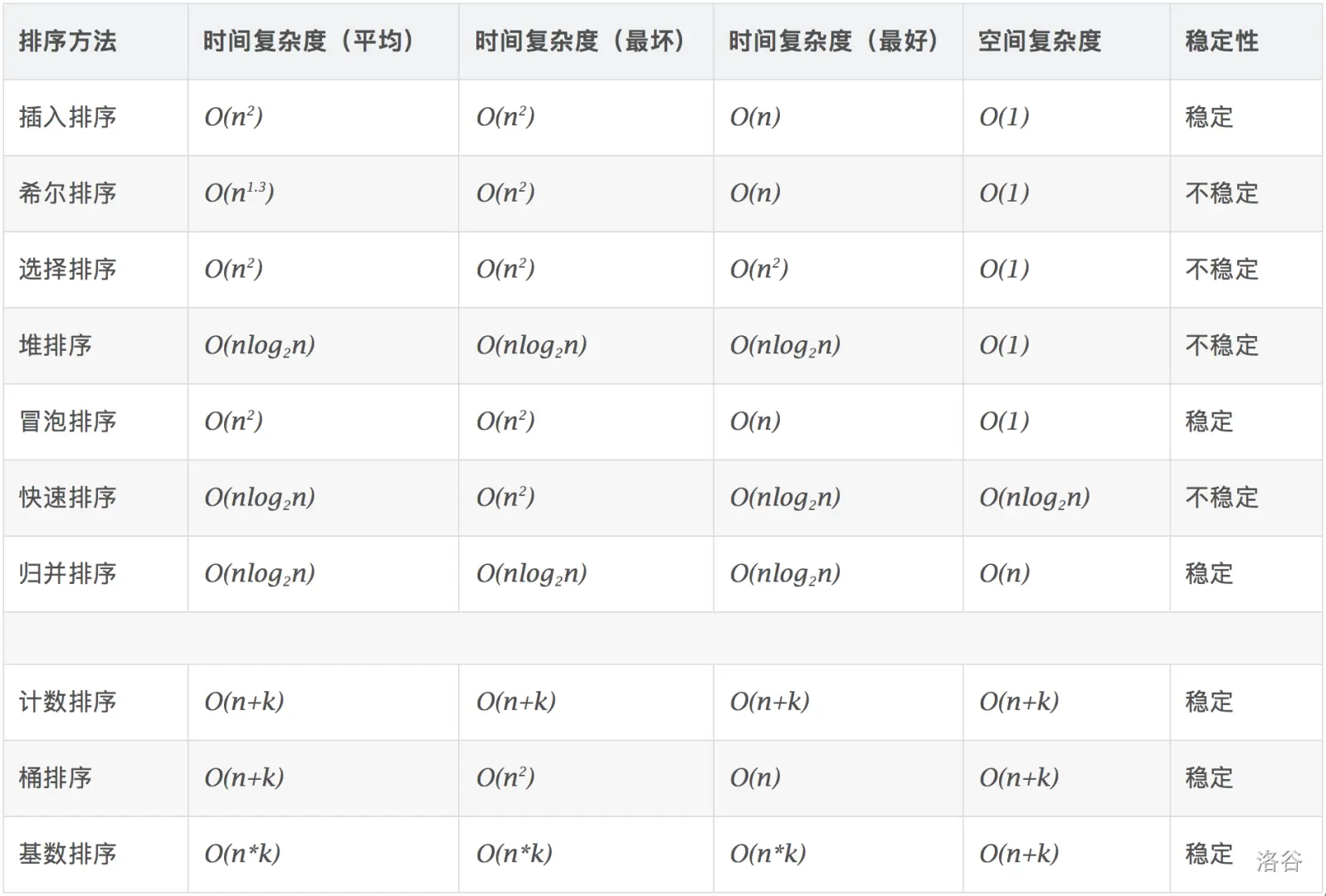
第 5 题
先两两比较,分成大的一组、小的一组。
最大值一定在大的一组,最小值一定在小的一组。
分别比较即可,次数为 \(n+(n-1)+(n-1)=3n-2\)。
为啥是最优?希腊奶。
第 6 题
模拟即可。
第 7 题
完全图有 \(\frac{n(n-1)}{2}\) 条边。
点数为 \(9\) 可以满足边数为 \(36\)。
但题目要求不连通,所以再加一个点,即点数为 \(10\)。
第 8 题
高度为 \(k\) 的满二叉树最多有 \(2^k-1\) 个点。记住 \(2^{10}=1024\),所以答案为 \(11\)。
第 9 题
前序遍历:根左右。
中序遍历:左根右。
所谓 “前”、“中”、“后” 就是根的位置。
故没有左儿子时相同。
第 10 题
即为原字符串的逆序对数。
证明,每次交换最多使逆序对数减小 \(1\)。且一定可以找到一对 \((a,b)\) 使得 \(a>b\),否则序列逆序对数为 \(0\)。
第 11 题
\(solve(t,n)=5^{t}\%n\)。
答案即为 \(5^{22}=5^0=1\)。
第 12 题
\(T(n)=T(n-1)+T(n-2)\)。也就是斐波那契数列,是指数级的。
第 13 题
考虑 DP,记 \(f_n\) 为 \(n\) 个苹果时的答案,则 \(f_1=1\) \(f_n=f_{n-1}+f_{n-2}+1\)(枚举最后一个苹果是否选择+只选择最后一个苹果)。
第 14 题
答案即为 \((a=b的三角形个数)+(b=c的)+(a=c的)-2(a=b=c的)=3(a=b)-18=3*61+18=165\)。
第 15 题
图为 DAG,拓扑排序即可(如果你能瞪出来也可)。
第 16 题
t<=sq(d2-d1) 后面为球的体积公式(\(acos(0.5)=\frac{\phi}{3}\))。
猜测 \(a,b,c\) 为球的中心坐标,\(d\) 为半径,程序求的是两个球的交的体积。
17.sqrt返回值是 double 类型,后除二不会下取整,先除二会。
19.呜呜,算错了。
第 17 题
看程序二,发现是最大子段和的分治写法,反代程序一发现也是。
25.\(T(n)=2T(\frac{n}{2})+O(1)\),根据主定理 \(T(n)=O(n)\)。
26.\(T(n)=2T(\frac{n}{2})+O(n)\),根据主定理 \(T(n)=O(nlogn)\)。
27.\(10\) 是 \(n\),某人眼瞎算出来答案为 \(24\)。
第 18 题
28.开除空串的字符串籍!
32.应该是 \(0xff=255\) 不太懂。懂了,char 占一个字节。
第 19 题
35.注意要求 \(f_n\),所以到 \(n\) 时停止。
第 20 题
考四毛子也是逆天。
但没啥细节吧。



