AGC032 A-D题解
A
最后一次插入的数的值与位置一定相同
考虑倒着做
每次从左往右扫一遍
当遇到 a[i]==i 时将此数删除并跳出
B
当 n 为 5 时
构造出的图如下
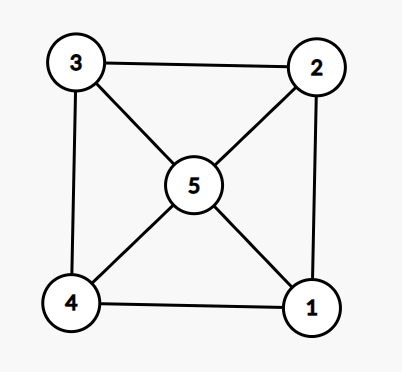
那么我们猜想当 n 为奇数时将 n 与其他点连边
i 与除了 n-i 的其他点连边
证明:
n 的邻接点的编号之和为 (n-1)*n/2
i 的邻接点的编号之和为 n*(n+1)/2-i-(n-i)=n*(n+1)/2-n=(n-1)*n/2
满足要求
当 n 为偶数时先按 n+1 连边再将 n+1 删掉即可
C
由于每个点都至少在一个环上,所以每个点的度数一定为偶数
当有一个点的度数大于等于 6 时一定合法
当所有点的度数都为 2 时一定不合法
再考虑点的度数为 2/4 的情况
当只有一个点的度数为 4 时 只能分成 2 个圈
当有两个点的度数为 4 时,通过画图可以发现,当两个度数为 4 的点有两条不相交路径相连时合法,四条则不合法
通过 dfs 判断即可
当度数为 4 的点大于 2 个时 一定合法
D
原操作可以转化为花费A将任意一个数移到该数的右边,花费B将任意一个数移到该数的左边
不难发现每个数最多会移动 1 次
可以将数分为移动的与不移动的
考虑 DP
设 f[i][j] 表示前 i 个数的移动以确定 j 为最后的不移动的数的值时的最小花费
将 f[i][i] 初始化为 A*(i-1) 其他为正无穷
当 a[i]<j 时 f[i][j]=min(f[i-1][j]+B)
当 a[i]>j 时 f[i][j]=min(f[i-1][j]+A) f[i][i]=min(f[i-1][j])
答案为 max(f[n][i]) (i:1->n)





