洛谷P3629 [APIO2010] 巡逻题解
题目链接
P3629 [APIO2010] 巡逻 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路
n个村庄，n-1条道路，原图为树
1.若k=0（不修建道路）
每个道路会走两遍
那么答案为（n-1）*2
2.若k为1（修建一条道路）
如下图a
可以看到r1（新建道路）所在的环只走了一次
所以答案为（n-1）*2-（环的长度-1（r1））-1（r1）
令答案最小，则是令环的长度最长
则道路应修建在直径的两个端点上
ans=（n-1）*2-直径的长度+1；
3.若k为2（修建2条道路）
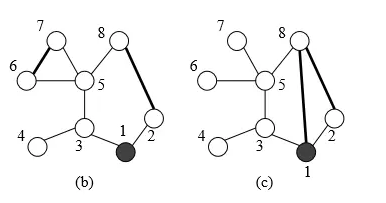
由b、c可知（或者自己手推）两条道路所在环可能有公共边或无公共边
当无公共边时（如图b）
发现两个环互不影响
当有公共边时（如图c）
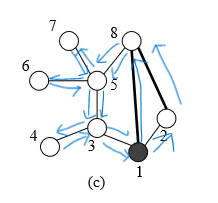
由于要满足必须经过新建的道路正好一次，两个环重复的地方仍要经过两次
那么将第一次计算的直径所经过的边权变成-1，这样若该边计入第二次直径，那么它对答案的贡献仍为2（一定经过两次）
综上
当k=1时ans=（n-1）*2-直径长+1；
当k=2时ans=（n-1）*2-第一次的直径长+1-第二次的直径长+1
代码
1 #include<bits/stdc++.h>
2 using namespace std;
3
4 const int N=100005;
5
6 int head[N],ne[N*2],v[N*2],w[N*2],tot=0;//链式前向星存图
7 void add(int x,int y,int z){
8 ne[++tot]=head[x];
9 v[tot]=y;
10 w[tot]=z;
11 head[x]=tot;
12 }
13
14
15 int l,ans=0;
16 int fa[N];//记录每个节点的父亲
17
18 void dfs(int u,int ffa,int dis){
19 if(dis>ans){
20 ans=dis;
21 l=u;
22 }
23 for(int i=head[u];i;i=ne[i]){
24 if(v[i]==ffa) continue;
25 fa[v[i]]=u;
26 dfs(v[i],u,dis+w[i]);
27 }
28 }
29
30 int f[N][2];
31 void solve(int u,int ffa){
32 for(int i=head[u];i;i=ne[i]){
33 int v1=v[i];
34 if(v1==ffa) continue;
35 solve(v1,u);
36 if(f[v1][0]+w[i]>=f[u][0]){
37 f[u][1]=f[u][0];
38 f[u][0]=f[v1][0]+w[i];
39 }
40 else if(f[v1][0]+w[i]>f[u][1]) f[u][1]=f[v1][0]+w[i];
41 }
42 }
43
44 int main(){
45 int n,k;
46 scanf("%d %d", &n, &k);
47 for(int i=1;i<n;i++){
48 int x,y;
49 scanf("%d %d", &x, &y);
50 add(x,y,1);
51 add(y,x,1);
52 }
53 //两次dfs求直径
54 dfs(1,0,0);
55 for(int i=1;i<=n;i++) fa[i]=0;
56 ans=0;
57 int r=l;
58 dfs(l,0,0);
59 //将直径上的边赋值为-1
60 while(fa[l]){
61 for(int i=head[l];i;i=ne[i]){
62 if(v[i]==fa[l]){
63 w[i]=-1;
64 if(i%2==0){
65 w[i-1]=-1;
66 }
67 else{
68 w[i+1]=-1;
69 }
70 break;
71 }
72 }
73 l=fa[l];
74 }
75 if(k==1){
76 cout<<(n-1)*2-ans+1;
77 return 0;
78 }
79 int l1=ans;
80 //dp求直径
81 solve(1,0);
82
83 ans=0;
84 for(int i=1;i<=n;i++) ans=max(ans,f[i][0]+f[i][1]);
85 cout<<n*2-l1-ans;
86
87 return 0;
88 }
