P4198 楼房重建
题目链接
分析
1.对于每栋楼，计算它顶点（x,y）与原点(0,0)连线的斜率（(double)y/x）那么能看到的楼则为斜率大的楼。
2.第一栋楼一定能被看见，那么问题就转化成了求从序列的第一项开始，后面每一项都选比前一项大的，能选则选，这样一个序列的长度
3.考虑用一个线段树来维护能看见的楼房数目
4.叶子节点长度为1
5.能看见的楼房数目->根节点的值
6.修建楼房->单点修改
7.如何合并呢？
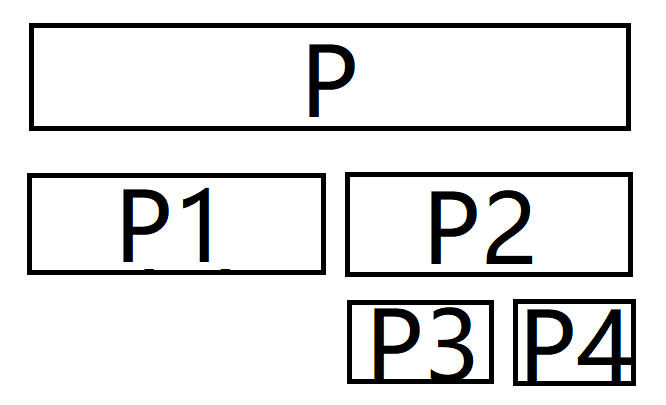
对于每个区间（P）它的左区间（P1）一定会被计算进去
那么右区间（P2）呢？
再维护区间的最大值（叶子节点的最大值为该点的斜率）
若右区间（P2）的左区间（P3）的最大值小于或等于左区间（P1）的最大值，那么P3一定不会被计算进去
所以递归进右区间（P2）的右区间（P4）进行计算
若右区间（P2）的左区间（P3）的最大值大于左区间（P1）的最大值
P3无法考虑，则递归进P3
P4对答案的贡献不能取P4的值，因为无法保证序列从第一项开始，它对答案的贡献应为 P2的值减P4的值
代码
1 #include<bits/stdc++.h>
2 using namespace std;
3
4 int n,m;
5
6 double tan(int x,int y){
7 return y*1.0/x;
8 }
9
10 int ans[100005*4];
11 double ma[100005*4];
12
13 int query(int p,int l,int r,double maxn){
14 if(ma[p]<=maxn) return 0;
15 int m=(l+r)>>1;
16 if(l==r) return 1;
17 else if(ma[p*2]<=maxn) return query(p*2+1,m+1,r,maxn);
18 return query(p*2,l,m,maxn)+ans[p]-ans[p*2];
19 }
20
21
22 void change(int p,int l,int r,int pc,double v){
23 if(l==pc&&r==pc){
24 ans[p]=1;
25 ma[p]=v;
26 return;
27 }
28 int m=(l+r)>>1;
29 if(pc<=m) change(p*2,l,m,pc,v);
30 else change(p*2+1,m+1,r,pc,v);
31 ma[p]=max(ma[p*2],ma[p*2+1]);
32 ans[p]=ans[p*2]+query(p*2+1,m+1,r,ma[p*2]);
33 }
34
35
36 int main(){
37 scanf("%d %d", &n, &m);
38 for(int i=1;i<=m;i++){
39 int x,y;
40 scanf("%d %d", &x, &y);
41 double a=tan(x,y);
42 change(1,1,n,x,a);
43 cout<<ans[1]<<endl;
44 }
45 return 0;
46 }
