灯塔 (数据结构）

灯塔(LightHouse)

---

Description

As shown in the following figure, If another lighthouse is in gray area, they can beacon each other.

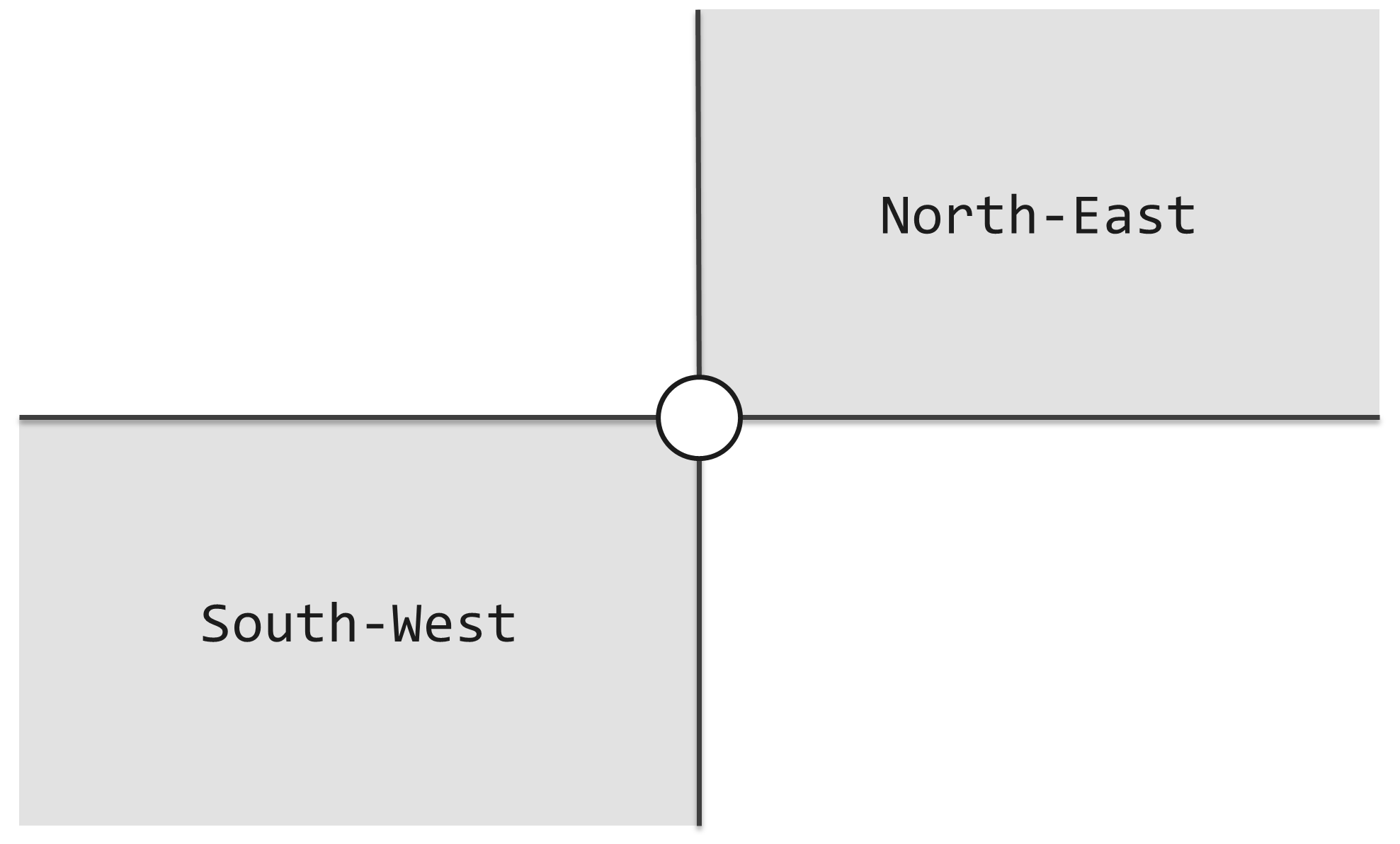
For example, in following figure, (B, R) is a pair of lighthouse which can beacon each other, while (B, G), (R, G) are NOT.

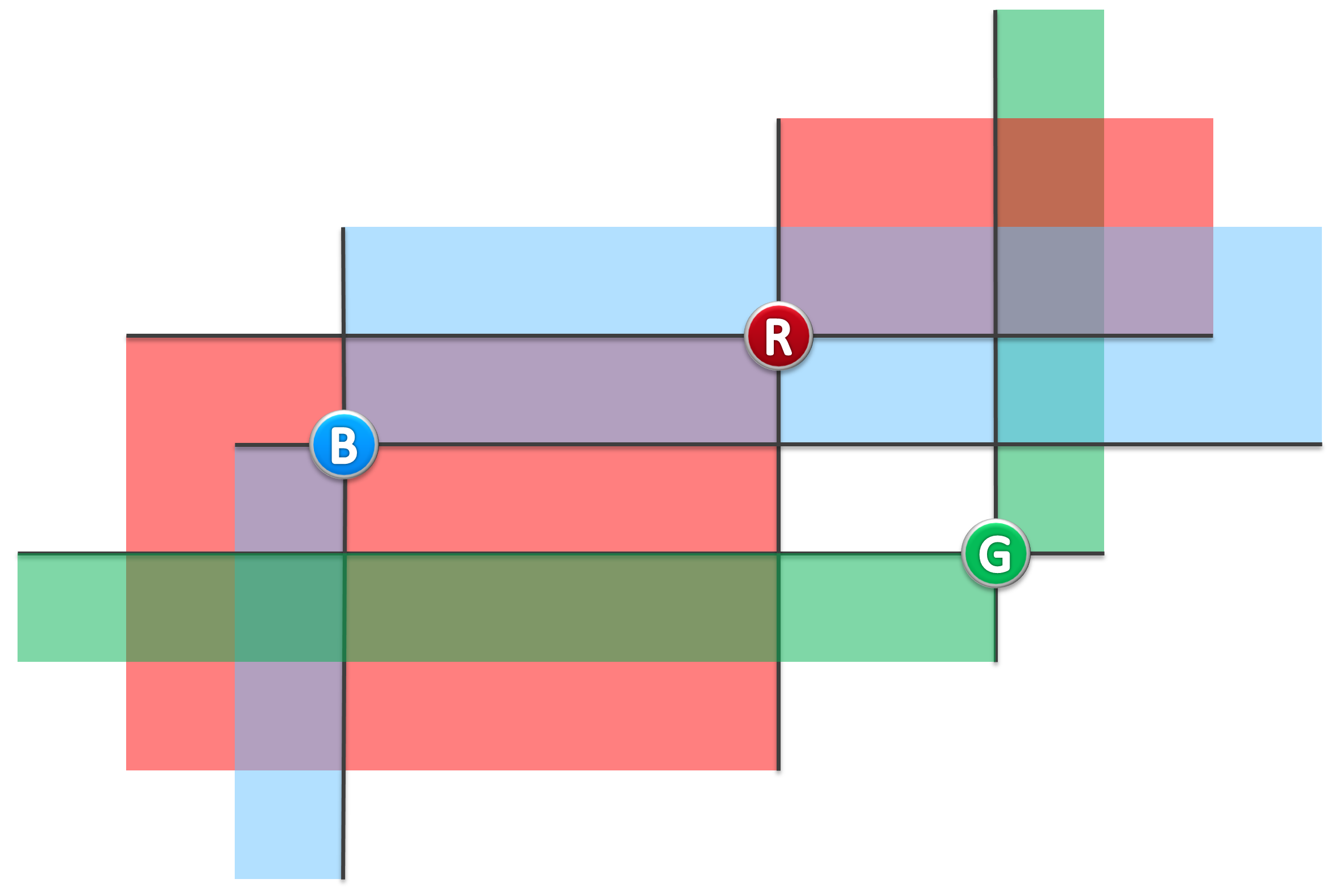
Input

1st line: N

2nd ~ (N + 1)th line: each line is X Y, means a lighthouse is on the point (X, Y).

Output

How many pairs of lighthourses can beacon each other

( For every lighthouses, X coordinates won't be the same , Y coordinates won't be the same )

Example

Input

3
2 2
4 3
5 1

Output

1

Restrictions

For 90% test cases: 1 <= n <= 3 * 105

For 95% test cases: 1 <= n <= 106

For all test cases: 1 <= n <= 4 * 106

For every lighthouses, X coordinates won't be the same , Y coordinates won't be the same.

1 <= x, y <= 10^8

Time: 2 sec

Memory: 256 MB

Hints

The range of int is usually [-231, 231 - 1], it may be too small.

 

解题思路：将灯塔按照x轴由大到小排序，即将问题转化为求y的逆序对的个数。求解逆序对可以利用归并排序的思路实现。

如下图：在某次归并的时候，左右两个数组已经排好顺序，如果遇到a[i] > a[j]，则，a[j] 与a[i] 到a[n]的所有元素均构成逆序对。

 

 

在归并排序的时候顺便统计一下逆序对的个数。

 注意，要统计的逆序对个数可能很大。

代码如下

 

#include<cstdio>
#include<cstring>
#define MAXN 4000005
#define ll long long 
using namespace std;

struct node{
    ll x;
    ll y;
} tower[MAXN];
ll des[MAXN];
struct node des1[MAXN];
int N;
ll num;
void merg(int l, int mid, int r)
{
    int i, j;
    int k;
    i = l;
    k = l;
    j = mid + 1;
    while(i <= mid && j <= r){
        if(tower[i].x < tower[j].x){
            des1[k].x = tower[i].x;
            des1[k++].y = tower[i++].y;
        }
        else{
            des1[k].x = tower[j].x;
            des1[k++].y = tower[j++].y;
        }
    }
    while(i <= mid){
        des1[k].x = tower[i].x;
        des1[k++].y = tower[i++].y;
    }
    while(j <= r){
        des1[k].x = tower[j].x;
        des1[k++].y = tower[j++].y;
    }

    for (i = l; i <= r; i++){
        tower[i].x = des1[i].x;
        tower[i].y = des1[i].y;
    }
}
void msort(int l, int r){
    if(l >= r - 1)
    {
        if(tower[l].x > tower[r].x){
            int x, y;
            x = tower[l].x;
            y = tower[l].y;
            tower[l].x = tower[r].x;
            tower[l].y = tower[r].y;
            tower[r].x = x;
            tower[r].y = y;
        }
        return;
    }
    int mid = (l + r) >> 1;
    msort(l, mid);
    msort(mid + 1, r);
    merg(l, mid, r);
}

void merge1(int l, int mid, int r)
{
    int i, j;
    ll cnt = 0;
    int k = l;
    i = l;
    j = mid + 1;
    while(i <= mid && j <= r){
        if(tower[i].y < tower[j].y){
            des[k++] = tower[i++].y;
            cnt += r - j + 1;
        }
        else{
            des[k++] = tower[j++].y;
        }
    }
    while(i <= mid)
        des[k++] = tower[i++].y;
    while(j <= r)
        des[k++] = tower[j++].y;
    for (i = l; i <= r; i++){
        tower[i].y = des[i];
    }
    num += cnt;
}
void get_num(int l, int r)
{
    if(l >= r - 1){
        if(tower[l].y < tower[r].y){
            num++;
        }
        else{
            int temp = tower[l].y;
            tower[l].y = tower[r].y;
            tower[r].y = temp;
        }
        return;
    }
    int mid = (l + r) >> 1;
    get_num(l, mid);
    get_num(mid + 1, r);
    merge1(l, mid, r);
}

int main()
{
    scanf("%d", &N);
    num = 0;
    for (int i = 0; i < N; i++)
    {
        scanf("%lld %lld", &tower[i].x, &tower[i].y);
    }
    msort(0, N - 1);
    get_num(0, N - 1);
    printf("%lld\n", num);
    
   
    return 0;
}