树篇3-平衡二叉查找树之红黑树
一、概述
红黑树是一种自平衡树在计算机科学中。二叉树的每个节点都有一个额外的位,该位通常被解释为节点的颜色(红色或黑色)。这些颜色位用于确保树在插入和删除期间保持近似平衡。通过以满足某些属性的方式用两种颜色之一绘制树的每个节点来保留平衡,这些属性共同限制树在最坏情况下的不平衡程度。修改树时,随后重新排列新树并重新绘制以恢复着色属性。这些属性的设计使得可以有效地执行这种重新排列和重新着色。树的平衡并不完美,但它足以保证在O(log n)时间内进行搜索,其中n是树中元素的总数。插入和删除操作以及树重新排列和重新着色也在O(log n)时间内执行。跟踪每个节点的颜色每个节点仅需要1位信息,因为只有两种颜色。该树不包含任何其他特定于红黑树的数据,因此其内存占用量几乎与经典(无色)二叉搜索树相同。在许多情况下,可以存储额外的信息,而无需额外的存储器成本。
二、属性
1.每个节点不是红色就是黑色。
2.根节点是黑色。(由根节点始终可以从红色变成黑色,所以这条规则对分析没影响)
3.所有叶子(NIL)都是黑的。
4.如果该节点是红色,则其两个孩子节点必须是黑色。(黑节点不要求两个孩子节点一定都是红)
5.从任意节点到任意可到达的叶子结点(NIL),路径中所包含的黑节点数目相同。(极其重要,这保证了红黑树是自平衡二叉树)
注释:
1)属性4和属性5保证了红黑树为自平衡二叉树。因此,保证红黑树满足4、5即可保证自平衡。
2)红黑树中从根节点到所有叶子节点的路径中,最长路径长度小于最短路径长度的二倍。
3)叶子节点NIL: 以往二叉树的根节点父指针域、节点的左右孩子域;有时到达树叶了,就会为空。在红黑树种,把空着的指针 域指向NIL节点,作为叶子节点。
三、红黑树的节点及整体
/**
* 红黑树
*/
public class RedBlackTree<T extends Comparable<T>> {
/**
* 红黑树节点
*/
static class RedBlackNode<T extends Comparable<T>> {
T key; // 节点值
boolean red; // 是否是红色节点
RedBlackNode<T> parent; // 父节点
RedBlackNode<T> leftChild; // 父节点
RedBlackNode<T> rightChild; // 父节点
public RedBlackNode() {
}
public RedBlackNode(T key) {
this();
this.key = key;
}
public boolean isRed() {
return red;
}
@Override
public String toString() {
return key + "";
}
}
private final RedBlackNode<T> NIL = new RedBlackNode<>(); // 哨兵节点(叶子结点)
private RedBlackNode<T> root = NIL; // 根节点
private int size; // 元素数量
public RedBlackTree() { // 构造方法
root.parent = NIL;
root.leftChild = NIL;
root.rightChild = NIL;
}
// 插入数据
public void insert(T key){}
private void insert(RedBlackNode<T> node) {}
// 插入修正
private void insertFixup(RedBlackNode<T> node) {}
// 右旋操作
private void rightRotate(RedBlackNode<T> node) {}
// 左旋操作
private void leftRotate(RedBlackNode<T> node) {}
// 判断节点是否是Nil(哨兵)
private boolean isNil(RedBlackNode<T> node) {}
// 遍历
public void preOrderErgodic(){}
public void preOrderErgodic(RedBlackNode node){}
// 返回树节点数
public int getSize() {}
// 移除节点
public void remove(T t) {}
// 移除节点
private void removeNode(RedBlackNode<T> v) {}
// 移除节点后修正
private void removeFixup(RedBlackNode<T> node) {}
// 获取后继
private RedBlackNode<T> treeSuccessor(RedBlackNode<T> waitRemoveNode) {}
// 获取以node为根节点的子树的最小节点
private RedBlackNode<T> treeMinimum(RedBlackNode<T> node) {}
// 根据值查找节点
private RedBlackNode<T> search(T key) {}
}四、插入操作
向红黑树中插入节点分两步完成:插入数据、根据红黑树性质对树进行修整。插入数据的方式和普通二叉树插入数据的方式相同,新插入的节点一定是红色节点;根据红黑树性质对树进行修整,是对红黑树进行颜色变换和旋转,是插入数据后,红黑树仍然满足上面的五条性质。
插入数据:
// 1.数据插入
private void insert(RedBlackNode<T> node) {
RedBlackNode<T> parent = NIL; // index的父节点
RedBlackNode<T> index = root; // 索引
while (!isNil(index)) { // 循环遍历,找到插入位置和父节点
parent = index;
if (node.key.compareTo(index.key) < 0) {
index = index.leftChild;
} else if (node.key.compareTo(index.key) > 0) {
index = index.rightChild;
} else { // 找到相等节点,结束程序
return;
}
}
// 将孩子指向父亲
node.parent = parent;
size++;
// 将父亲指向孩子,分情况讨论:
// 1.父节点是NIL(当前树为空,没有根节点)
if (isNil(parent))
root = node;
// 2.父亲的左孩子
else if (node.key.compareTo(parent.key) < 0)
parent.leftChild = node;
// 3.父亲的右孩子
else
parent.rightChild = node;
// 初始化孩子和颜色(新添加的节点一定是红色)
node.leftChild = NIL;
node.rightChild = NIL;
node.red = true;
// 2.红黑树插入修正
insertFixup(node);
}红黑树修正分一下四种情况:
情况1:新插入节点N为根节点
// 颜色根部始终为黑色
// 情况1:新插入节点N为根节点
root.red = false;情况2:新插入节点N的父节点为黑色
如果N节点的父亲是黑节点,此时插入新节点N对树没有任何影响,此时树依旧满足红黑树的五条性质。因此不要做任何操作。
情况3:新插入节点N的父节点为红色,叔节点(父亲的兄弟节点)为红色
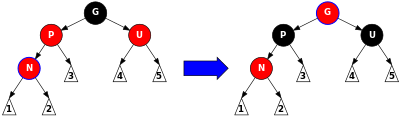
// 情况3.cousinNode(叔叔节点)是红节点
if (cousinNode.isRed()) {
node.parent.red = false; // node父节点置为黑
cousinNode.red = false; // node叔节点置为黑
node.parent.parent.red = true; // node的爷爷节点置红
node = node.parent.parent;
}情况4:新插入节点N的父节点为红色,叔节点(父亲的兄弟节点)为黑色
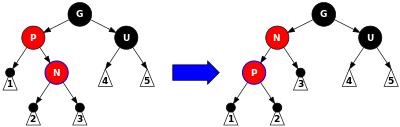
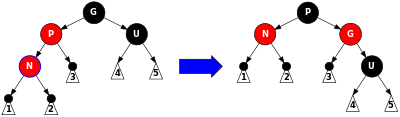
// 情况4.cousinNode节点为[黑节点]且为父节点[左孩子]
else if (node == node.parent.leftChild) {
// 重置颜色、以node的爷爷旋转
node.parent.red = false;
node.parent.parent.red = true;
rightRotate(node.parent.parent);
}
// 情况4.cousinNode节点为[黑节点]且为父节点[右孩子]
else {
// 以node的父亲左旋
node = node.parent;
leftRotate(node);
}完整的插入后修正代码如下:
/**
* 插入修正
*
* @param node 插入的节点
*/
private void insertFixup(RedBlackNode<T> node) {
RedBlackNode<T> cousinNode = NIL; //叔节点
// 循环修正节点
// 新插入节点的父亲为红色,则不满足性质4(如果该节点是红色,则其两个孩子节点必须是黑色)
while (node.parent.isRed()) {
// node节点的 [父亲] 是 [爷爷] 节点的 [左孩子]
if (node.parent == node.parent.parent.leftChild) {
// 初始化node的叔叔(父节点的兄弟)
cousinNode = node.parent.parent.rightChild;
// 情况3.cousinNode(叔叔节点)是红节点
if (cousinNode.isRed()) {
node.parent.red = false; // node父节点置为黑
cousinNode.red = false; // node叔节点置为黑
node.parent.parent.red = true; // node的爷爷节点置红
node = node.parent.parent;
}
// 情况4.cousinNode节点为[黑节点]且为父节点[左孩子]
else if (node == node.parent.leftChild) {
// 重置颜色、以node的爷爷旋转
node.parent.red = false;
node.parent.parent.red = true;
rightRotate(node.parent.parent);
}
// 情况4.cousinNode节点为[黑节点]且为父节点[右孩子]
else {
// 以node的父亲左旋
node = node.parent;
leftRotate(node);
}
}
// node节点的 [父亲] 是 [爷爷] 节点的 [右孩子]
else {
// 初始化node的叔叔(父节点的兄弟)
cousinNode = node.parent.parent.leftChild;
// 情况1.cousinNode(叔叔节点)是红节点
if (cousinNode.isRed()) {
node.parent.red = false; // node父节点置为黑
cousinNode.red = false; // node叔节点置为黑
node.parent.parent.red = true; // node的爷爷节点置红
node = node.parent.parent;
}
// 情况2.cousinNode节点为[黑节点]且为父节点[左孩子]
else if (node == node.parent.leftChild) {
node = node.parent;
// 以node的父亲右旋
rightRotate(node);
}
// 情况3.cousinNode节点为[黑节点]且为父节点[右孩子]
else {
// 重置颜色、以node的爷爷旋转
node.parent.red = false;
node.parent.parent.red = true;
leftRotate(node.parent.parent);
}
}
}
// 颜色根部始终为黑色
// 情况1:新插入节点N为根节点
root.red = false;
}五、左旋和右旋操作
当插入数据后,需要对树进行修复使其满足红黑树的五条性质;在修复的过程中,需要对节点的位置进行调整,这是就要使用左旋和右旋操作。
/**
* 左旋操作
*
* @param node 旋转的轴节点
*/
private void leftRotate(RedBlackNode<T> node) {
RedBlackNode<T> nodeRightChild = node.rightChild; // node的右孩子
node.rightChild = nodeRightChild.leftChild; // 将node的右孩子的左孩子过继给node,作为它的右孩子
if (!isNil(nodeRightChild.leftChild)) // node的右孩子的左孩子不为NIL
nodeRightChild.leftChild.parent = node; // 将node作为它的父亲
nodeRightChild.parent = node.parent; // 将nodeRightChild的父域指向node的父亲
// 如果node的父亲NIL
if (isNil(node.parent))
root = nodeRightChild;
// node是其父节点的左孩子
else if (node.parent.leftChild == node)
node.parent.leftChild = nodeRightChild;
// node是其父节点的右孩子
else
node.parent.rightChild = nodeRightChild;
// 最后的旋转
nodeRightChild.leftChild = node;
node.parent = nodeRightChild;
}
/**
* 右旋操作
*
* @param node 旋转的轴节点
*/
private void rightRotate(RedBlackNode<T> node) {
RedBlackNode<T> nodeLeftChild = node.leftChild; // node左孩子
node.leftChild = nodeLeftChild.rightChild; // 将node的左孩子的右孩子过继给node,作为它的左孩子
if (!isNil(nodeLeftChild.rightChild)) // node的左孩子的右孩子不为NIL
nodeLeftChild.rightChild.parent = node; // 将node作为它的父亲
nodeLeftChild.parent = node.parent; // 将nodeLeftChild的父域指向node的父亲
// 如果node的父亲NIL
if (isNil(node.parent))
root = nodeLeftChild;
// node是其父节点的左孩子
else if (node.parent.leftChild == node)
node.parent.leftChild = nodeLeftChild;
// node是其父节点的右孩子
else
node.parent.rightChild = nodeLeftChild;
// 最后的旋转
nodeLeftChild.rightChild = node;
node.parent = nodeLeftChild;
}六、删除节点
删除节点的操作与插入相似,直接上代码
// 移除节点
private void removeNode(RedBlackNode<T> v) {
RedBlackNode<T> waitRemoveNode = search(v.key); // 查找待删除节点
RedBlackNode<T> successorNode = NIL; // 后继节点
RedBlackNode<T> successorChild = NIL; // 后继的子节点
// waitRemoveNode没有孩子节点,或者有一个孩子节点的情况
if (isNil(waitRemoveNode.leftChild) || isNil(waitRemoveNode.rightChild))
successorNode = waitRemoveNode;
else // waitRemoveNode有两个孩子节点的情况
successorNode = treeSuccessor(waitRemoveNode);
if (!isNil(successorNode.leftChild)) // 获取后继的孩子
successorChild = successorNode.leftChild;
else
successorChild = successorNode.rightChild;
successorChild.parent = successorNode.parent; //successorChild父域指向successorNode父亲
if (isNil(successorNode.parent)) // 如果successorNode父亲为空
root = successorChild;
// 左孩子
else if (!isNil(successorNode.parent.leftChild) && successorNode.parent.leftChild == successorNode)
successorNode.parent.leftChild = successorChild;
// 右孩子
else if (!isNil(successorNode.parent.rightChild) && successorNode.parent.rightChild == successorNode)
successorNode.parent.rightChild = successorChild;
// 待删除节点已从树中移除,复制值
if (successorNode != waitRemoveNode)
waitRemoveNode.key = successorNode.key;
if (!successorNode.red) // 如果后继为黑节点,需要平衡红黑树
removeFixup(successorChild);
}
/**
* 删除节点后修复红黑树
*
* @param node 为黑色的后继节点
*/
private void removeFixup(RedBlackNode<T> node) {
RedBlackNode<T> nodeBrothers; // node的兄弟节点
// node不是根节点,且颜色为黑色
while (node != root && node.red == false) {
// 如果node是其父亲的左孩子
if (node.parent.leftChild == node) {
nodeBrothers = node.parent.rightChild; // node父亲的右孩子即为node的兄弟
// 1.node兄弟节点为红色
if (nodeBrothers.red == true) {
nodeBrothers.red = false;
nodeBrothers.parent.red = true;
leftRotate(nodeBrothers.parent);
nodeBrothers = node.parent.rightChild;
}
// 2.node兄弟节点的左右孩子都为黑色
if (nodeBrothers.leftChild.red == false && nodeBrothers.rightChild.red == false) {
nodeBrothers.red = true;
node = node.parent;
} else {
// 3.node兄弟节点的右孩子为黑色
if (nodeBrothers.rightChild.red == false) {
nodeBrothers.leftChild.red = false;
nodeBrothers.red = true;
rightRotate(nodeBrothers);
nodeBrothers = node.parent.rightChild;
}
// 4.node兄弟节点为黑色, node兄弟节点的右孩子为红色
nodeBrothers.red = node.parent.red;
node.parent.red = false;
nodeBrothers.rightChild.red = false;
leftRotate(node.parent);
node = root;
}
}
// node是父亲的右孩子
else {
nodeBrothers = node.parent.leftChild; // node父亲的左孩子即为node的兄弟
// 1.nodeBrothers为红色
if (nodeBrothers.red == true) {
nodeBrothers.red = false;
nodeBrothers.parent.red = true;
rightRotate(nodeBrothers.parent);
nodeBrothers = node.parent.leftChild;
}
// 2.nodeBrothers的孩子节点都是黑色
if (nodeBrothers.leftChild.red == false && nodeBrothers.rightChild.red == false) {
nodeBrothers.red = true;
node = node.parent;
} else {
// 3.nodeBrothers的左孩子是黑色
if (nodeBrothers.leftChild.red == false) {
nodeBrothers.rightChild.red = false;
nodeBrothers.red = true;
leftRotate(nodeBrothers);
nodeBrothers = node.parent.leftChild;
}
// 4.nodeBrothers是黑色,nodeBrothers的左孩子是红色
nodeBrothers.red = node.parent.red;
node.parent.red = false;
nodeBrothers.leftChild.red = false;
rightRotate(node.parent);
node = root;
}
}
}
// 设置节点为黑色,保证满足红黑树的特性
node.red = false;
}
private RedBlackNode<T> treeSuccessor(RedBlackNode<T> waitRemoveNode) {
if (!isNil(waitRemoveNode.leftChild))
return treeMinimum(waitRemoveNode.rightChild);
return null;
}
// 获取以node为根节点的子树的最小节点
private RedBlackNode<T> treeMinimum(RedBlackNode<T> node) {
while (!isNil(node.leftChild))
node = node.leftChild;
return node;
}七、完整版代码如下
import com.sun.org.apache.xalan.internal.xsltc.dom.NodeIteratorBase;
import org.hamcrest.core.IsNull;
/**
* 红黑树
*/
public class RedBlackTree<T extends Comparable<T>> {
/**
* 红黑树节点
*/
static class RedBlackNode<T extends Comparable<T>> {
T key; // 节点值
boolean red; // 是否是红色节点
RedBlackNode<T> parent; // 父节点
RedBlackNode<T> leftChild; // 父节点
RedBlackNode<T> rightChild; // 父节点
public RedBlackNode() {
}
public RedBlackNode(T key) {
this();
this.key = key;
}
public boolean isRed() {
return red;
}
@Override
public String toString() {
return key + "";
}
}
private final RedBlackNode<T> NIL = new RedBlackNode<>(); // 哨兵节点(叶子结点)
private RedBlackNode<T> root = NIL; // 根节点
private int size; // 元素数量
public RedBlackTree() { // 构造方法
root.parent = NIL;
root.leftChild = NIL;
root.rightChild = NIL;
}
// 插入数据分两步:1.数据插入 2.根据红黑树性质修正树
public void insert(T key) {
if (key == null || key == "") // 数据检查
return;
insert(new RedBlackNode<T>(key));
}
// 1.数据插入
private void insert(RedBlackNode<T> node) {
RedBlackNode<T> parent = NIL; // index的父节点
RedBlackNode<T> index = root; // 索引
while (!isNil(index)) { // 循环遍历,找到插入位置和父节点
parent = index;
if (node.key.compareTo(index.key) < 0) {
index = index.leftChild;
} else if (node.key.compareTo(index.key) > 0) {
index = index.rightChild;
} else { // 找到相等节点,结束程序
return;
}
}
// 将孩子指向父亲
node.parent = parent;
size++;
// 将父亲指向孩子,分情况讨论:
// 1.父节点是NIL(当前树为空,没有根节点)
if (isNil(parent))
root = node;
// 2.父亲的左孩子
else if (node.key.compareTo(parent.key) < 0)
parent.leftChild = node;
// 3.父亲的右孩子
else
parent.rightChild = node;
// 初始化孩子和颜色(新添加的节点一定是红色)
node.leftChild = NIL;
node.rightChild = NIL;
node.red = true;
// 2.红黑树插入修正
insertFixup(node);
}
/**
* 插入修正
*
* @param node 插入的节点
*/
private void insertFixup(RedBlackNode<T> node) {
RedBlackNode<T> cousinNode = NIL; //叔节点
// 循环修正节点
// 新插入节点的父亲为红色,则不满足性质4(如果该节点是红色,则其两个孩子节点必须是黑色)
while (node.parent.isRed()) {
// node节点的 [父亲] 是 [爷爷] 节点的 [左孩子]
if (node.parent == node.parent.parent.leftChild) {
// 初始化node的叔叔(父节点的兄弟)
cousinNode = node.parent.parent.rightChild;
// 情况3.cousinNode(叔叔节点)是红节点
if (cousinNode.isRed()) {
node.parent.red = false; // node父节点置为黑
cousinNode.red = false; // node叔节点置为黑
node.parent.parent.red = true; // node的爷爷节点置红
node = node.parent.parent;
}
// 情况4.cousinNode节点为[黑节点]且为父节点[左孩子]
else if (node == node.parent.leftChild) {
// 重置颜色、以node的爷爷旋转
node.parent.red = false;
node.parent.parent.red = true;
rightRotate(node.parent.parent);
}
// 情况4.cousinNode节点为[黑节点]且为父节点[右孩子]
else {
// 以node的父亲左旋
node = node.parent;
leftRotate(node);
}
}
// node节点的 [父亲] 是 [爷爷] 节点的 [右孩子]
else {
// 初始化node的叔叔(父节点的兄弟)
cousinNode = node.parent.parent.leftChild;
// 情况1.cousinNode(叔叔节点)是红节点
if (cousinNode.isRed()) {
node.parent.red = false; // node父节点置为黑
cousinNode.red = false; // node叔节点置为黑
node.parent.parent.red = true; // node的爷爷节点置红
node = node.parent.parent;
}
// 情况2.cousinNode节点为[黑节点]且为父节点[左孩子]
else if (node == node.parent.leftChild) {
node = node.parent;
// 以node的父亲右旋
rightRotate(node);
}
// 情况3.cousinNode节点为[黑节点]且为父节点[右孩子]
else {
// 重置颜色、以node的爷爷旋转
node.parent.red = false;
node.parent.parent.red = true;
leftRotate(node.parent.parent);
}
}
}
// 颜色根部始终为黑色
// 情况1:新插入节点N为根节点
root.red = false;
}
/**
* 右旋操作
*
* @param node 旋转的轴节点
*/
private void rightRotate(RedBlackNode<T> node) {
RedBlackNode<T> nodeLeftChild = node.leftChild; // node左孩子
node.leftChild = nodeLeftChild.rightChild; // 将node的左孩子的右孩子过继给node,作为它的左孩子
if (!isNil(nodeLeftChild.rightChild)) // node的左孩子的右孩子不为NIL
nodeLeftChild.rightChild.parent = node; // 将node作为它的父亲
nodeLeftChild.parent = node.parent; // 将nodeLeftChild的父域指向node的父亲
// 如果node的父亲NIL
if (isNil(node.parent))
root = nodeLeftChild;
// node是其父节点的左孩子
else if (node.parent.leftChild == node)
node.parent.leftChild = nodeLeftChild;
// node是其父节点的右孩子
else
node.parent.rightChild = nodeLeftChild;
// 最后的旋转
nodeLeftChild.rightChild = node;
node.parent = nodeLeftChild;
}
/**
* 左旋操作
*
* @param node 旋转的轴节点
*/
private void leftRotate(RedBlackNode<T> node) {
RedBlackNode<T> nodeRightChild = node.rightChild; // node的右孩子
node.rightChild = nodeRightChild.leftChild; // 将node的右孩子的左孩子过继给node,作为它的右孩子
if (!isNil(nodeRightChild.leftChild)) // node的右孩子的左孩子不为NIL
nodeRightChild.leftChild.parent = node; // 将node作为它的父亲
nodeRightChild.parent = node.parent; // 将nodeRightChild的父域指向node的父亲
// 如果node的父亲NIL
if (isNil(node.parent))
root = nodeRightChild;
// node是其父节点的左孩子
else if (node.parent.leftChild == node)
node.parent.leftChild = nodeRightChild;
// node是其父节点的右孩子
else
node.parent.rightChild = nodeRightChild;
// 最后的旋转
nodeRightChild.leftChild = node;
node.parent = nodeRightChild;
}
// 判断节点是否是Nil(哨兵)
private boolean isNil(RedBlackNode<T> node) {
return node == this.NIL;
}
public void preOrderErgodic(){
preOrderErgodic(this.root);
}
/**
* 前序遍历红黑树
* @param node
*/
public void preOrderErgodic(RedBlackNode node){
if (node != this.NIL) {
System.out.print(node.key + "\tC:" + (node.red ? "Red" : "Black") + "\t\t");
if (node.leftChild != this.NIL)
System.out.print( "(L)" + node.leftChild.key + "\t\t");
else
System.out.print("(L)Null\t\t");
if (node.rightChild != this.NIL)
System.out.print("(R)" + node.rightChild.key + "\t\t");
else
System.out.print("(R)Null\t\t");
System.out.println();
preOrderErgodic(node.leftChild);
preOrderErgodic(node.rightChild);
}
}
// 返回树节点数
public int getSize() {
return size;
}
/**
* 删除节点
*
* @param t 要删除的节点
*/
public void remove(T t) {
if (t == null || t == "") // 简单的错误检查
return;
removeNode(new RedBlackNode<T>(t));
size--;
}
// 移除节点
private void removeNode(RedBlackNode<T> v) {
RedBlackNode<T> waitRemoveNode = search(v.key); // 查找待删除节点
RedBlackNode<T> successorNode = NIL; // 后继节点
RedBlackNode<T> successorChild = NIL; // 后继的子节点
// waitRemoveNode没有孩子节点,或者有一个孩子节点的情况
if (isNil(waitRemoveNode.leftChild) || isNil(waitRemoveNode.rightChild))
successorNode = waitRemoveNode;
else // waitRemoveNode有两个孩子节点的情况
successorNode = treeSuccessor(waitRemoveNode);
if (!isNil(successorNode.leftChild)) // 获取后继的孩子
successorChild = successorNode.leftChild;
else
successorChild = successorNode.rightChild;
successorChild.parent = successorNode.parent; //successorChild父域指向successorNode父亲
if (isNil(successorNode.parent)) // 如果successorNode父亲为空
root = successorChild;
// 左孩子
else if (!isNil(successorNode.parent.leftChild) && successorNode.parent.leftChild == successorNode)
successorNode.parent.leftChild = successorChild;
// 右孩子
else if (!isNil(successorNode.parent.rightChild) && successorNode.parent.rightChild == successorNode)
successorNode.parent.rightChild = successorChild;
// 待删除节点已从树中移除,复制值
if (successorNode != waitRemoveNode)
waitRemoveNode.key = successorNode.key;
if (!successorNode.red) // 如果后继为黑节点,需要平衡红黑树
removeFixup(successorChild);
}
/**
* 删除节点后修复红黑树
*
* @param node 为黑色的后继节点
*/
private void removeFixup(RedBlackNode<T> node) {
RedBlackNode<T> nodeBrothers; // node的兄弟节点
// node不是根节点,且颜色为黑色
while (node != root && node.red == false) {
// 如果node是其父亲的左孩子
if (node.parent.leftChild == node) {
nodeBrothers = node.parent.rightChild; // node父亲的右孩子即为node的兄弟
// 1.node兄弟节点为红色
if (nodeBrothers.red == true) {
nodeBrothers.red = false;
nodeBrothers.parent.red = true;
leftRotate(nodeBrothers.parent);
nodeBrothers = node.parent.rightChild;
}
// 2.node兄弟节点的左右孩子都为黑色
if (nodeBrothers.leftChild.red == false && nodeBrothers.rightChild.red == false) {
nodeBrothers.red = true;
node = node.parent;
} else {
// 3.node兄弟节点的右孩子为黑色
if (nodeBrothers.rightChild.red == false) {
nodeBrothers.leftChild.red = false;
nodeBrothers.red = true;
rightRotate(nodeBrothers);
nodeBrothers = node.parent.rightChild;
}
// 4.node兄弟节点为黑色, node兄弟节点的右孩子为红色
nodeBrothers.red = node.parent.red;
node.parent.red = false;
nodeBrothers.rightChild.red = false;
leftRotate(node.parent);
node = root;
}
}
// node是父亲的右孩子
else {
nodeBrothers = node.parent.leftChild; // node父亲的左孩子即为node的兄弟
// 1.nodeBrothers为红色
if (nodeBrothers.red == true) {
nodeBrothers.red = false;
nodeBrothers.parent.red = true;
rightRotate(nodeBrothers.parent);
nodeBrothers = node.parent.leftChild;
}
// 2.nodeBrothers的孩子节点都是黑色
if (nodeBrothers.leftChild.red == false && nodeBrothers.rightChild.red == false) {
nodeBrothers.red = true;
node = node.parent;
} else {
// 3.nodeBrothers的左孩子是黑色
if (nodeBrothers.leftChild.red == false) {
nodeBrothers.rightChild.red = false;
nodeBrothers.red = true;
leftRotate(nodeBrothers);
nodeBrothers = node.parent.leftChild;
}
// 4.nodeBrothers是黑色,nodeBrothers的左孩子是红色
nodeBrothers.red = node.parent.red;
node.parent.red = false;
nodeBrothers.leftChild.red = false;
rightRotate(node.parent);
node = root;
}
}
}
// 设置节点为黑色,保证满足红黑树的特性
node.red = false;
}
private RedBlackNode<T> treeSuccessor(RedBlackNode<T> waitRemoveNode) {
if (!isNil(waitRemoveNode.leftChild))
return treeMinimum(waitRemoveNode.rightChild);
return null;
}
// 获取以node为根节点的子树的最小节点
private RedBlackNode<T> treeMinimum(RedBlackNode<T> node) {
while (!isNil(node.leftChild))
node = node.leftChild;
return node;
}
/**
* 根据值寻找节点
*
* @param key 指定的值
* @return 节点
*/
private RedBlackNode<T> search(T key) {
RedBlackNode<T> index = root; // 指针
while (!isNil(index)) { // 循环遍历
if (key.equals(index.key)) // 找到了直接返回
return index;
else if (key.compareTo(index.key) < 0) // 小于取左
index = index.leftChild;
else // 大于取右
index = index.rightChild;
}
return null; // 未找到节点返回null
}
}
测试代码如下:
public class RedBlackTreeDemo {
public static void main(String[] args) {
RedBlackTree tree = new RedBlackTree();
// tree.insert(10);
// tree.insert(9);
// tree.insert(8);
// tree.insert(7);
// tree.insert(6);
// tree.insert(5);
// tree.insert(4);
// tree.insert(3);
// tree.insert(2);
// tree.insert(1);
tree.insert(40);
tree.insert(30);
tree.insert(50);
tree.insert(25);
tree.insert(51);
tree.insert(66);
tree.insert(66);
System.out.println("The number of node in the tree: " + tree.getSize());
tree.preOrderErgodic();
// tree.remove(7);
tree.remove(40);
System.out.println("The number of node in the tree: " + tree.getSize());
tree.preOrderErgodic();
}
}八、参考
https://github.com/Arsenalist/Red-Black-Tree-Java-Implementation/blob/master/README



 浙公网安备 33010602011771号
浙公网安备 33010602011771号