归纳法证明欧几里得算法

前言

    本证明思路来源于 《数学分析 Apostol》 定理 1.6

每一对非负整数a与b都有一个公因数d，形为

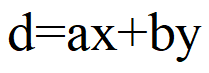
其中x和y都是整数，且a，b的每一个公因数都能整除这个d（显然这个d就是最大公因数）

证明

    设 且

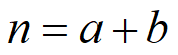
    由对称性，不妨设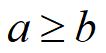

        Step.1

            当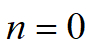时

            

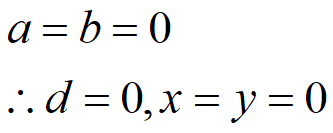
        Step.2

            假设n=0，1，2，3，…，k-1时，定理已经证明

                n=a+b=k时

1. b=0,则令 d=a,x=1,y=0，定理成立
2. 

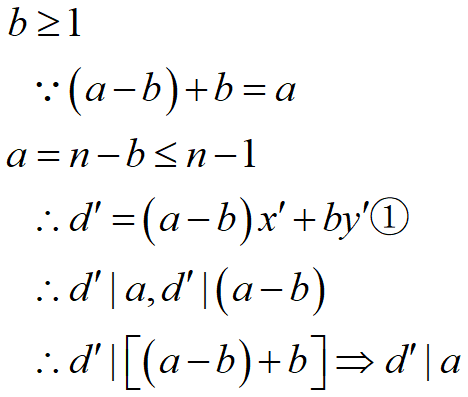
   综上 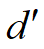为a,b的公因数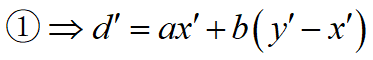

   

                 设t为a，b的某一公因数

                

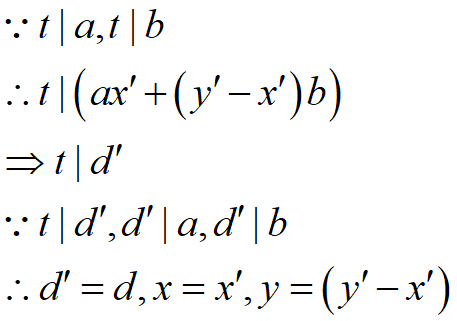
                n=k时，定理依旧成立

定理1.6证毕

代码

 

#include <iostream>
using namespace std;

void exgcd(int a, int b, int &x, int &y, int &d) {
  if (a < b)
    swap(a, b);
  if (b == 0) {
    d = a, x = 1, y = 0;
    return;
  } else {
    int _x, _y, _d;
    exgcd(a - b, b, _x, _y, _d);
    x = _x, d = _d, y = _y - _x;
  }
}

int main() {
  int x = 0, y = 0, d = 0;
  exgcd(20, 15, x, y, d);
  cout << x << ' ' << y << ' ' << d;
}