图论随手记 - 最短路
顺序有点乱，后续会排一下，然后分板块整理
All
-
最短路算法的选择：
\(n \le 100\) ： Floyd（一般是较难的图论建模）
\(n \le 4 \times 10 ^ 5\): dijkstra
尽量不用 SPFA。
-
神秘 IDEA: 一个带负权图，绝对最短路定义为，绝对值最小的最短路，求 \(s \to t\) 的绝对最短路。
-
最短路中，任意一个点的前缀都是最短路。
具体的： \(u \to v\) 的最短路中有一个点 \(w\)，那么 \(u \to w\) 的最短路，也在此条路径中。
Dijkstra
-
Dijkstra = 贪心 + DP
时间复杂度： \(\text{O}(m \log m)\) -
证： 在 Dijkstra 算法过程中，每次找出 \(dis\) 最小的没有被确定最短路的点，它的 dis 一定是源点到它的最短路。
注意：正难则反 \(\to\) 反证法
证明： 设 \(S\) 集合表示最短路已经确定的点， \(T\) 集合表示最短路还没有确定的点。
即证： \(T\) 集合中 \(dis\) 最小的元素可以直接加入到 \(S\) 集合中。
所以 \(dis\) 中储存的数值， 为从源点到 \(u\)，只经过 \(S\) 集合中的点所得到的最短路。
反证：
设当前 \(T\) 集合中 \(dis\) 最小的元素为 \(u\)，且 \(dis_{u}\) 不为源点到 \(u\) 的最短路。
如果有一条更短的最短路， 那么，这两条路径中至少要有一个点不同。
设最早不同的点为，\(v_1\) 和 \(v_2\)，\(v_2\) 为更短最短路中的一个点， \(v_1\) 为当前路径中的一个点。
当且仅当，\(v_2\) 在 \(T\) 集合中，才会没有被更新到。
又因为，dijkstra 只能处理非负权图。（这里也可以说明为什么 dijkstra 只能处理非负权图）
所以， \(dis_{v_2}\) 只能小于 \(dis_u\) 才能更新到 \(u\)。（如果有负权，这里会出问题）
发现，这与 \(dis_u\) 为 \(T\) 集合中最小的元素矛盾。
所以，不存在 \(v_2\)。
得证
-
有的时候，dijkstra 堆优化是负优化。
Eg. \(m = n ^ 2\)
时间复杂度为： \(O(n^2 \log n^2)\)，不如暴力的 \(O(n ^ 2)\)。
Bellman Ford
-
Bellman Ford(可优化为容易被卡的 SPFA)
优点： 可以处理负权，简单
缺点： 慢
时间复杂度： \(\text{O}(nm)\)
Floyd
-
有关 Floyd 的题目主要需要考虑 Floyd 中能提供的信息，而不能只看到 Floyd 提供的任意两点之间的最短路或者是传递闭包。 （TODO： Floyd 深度理解 【坑 ++】）
-
Floyd 跑3遍，任意循环顺序都可以求出全源最短路。
-
证明： Floyd 的 \(k, i, j\) 枚举顺序为什么可行？
回归 Floyd 的本初，原本为 DP，状态为 \(dp[k][i][j]\) ：仅前 \(k\) 个点， \(i \to j\) 的最短路。
\[dp[k][i][j] = \min(dp[k][i][j], dp[k - 1][i][k] + dp[k - 1][k][j]) \]此时,显然可行。
怎么滚动掉第一维的？
在 DP 的角度上看，这样的滚动是会使用到更新过的值，而非使用上一轮的数据。
但是，这里 \(dp_{k, i, k}\) 由于其中不经过 \(k\)，所以等价于 \(dp_{k - 1,i,k}\)，覆盖了也没关系，所以只要原先状态与覆盖状态意义相同，则同样可以使用滚动数组。
-
Floyd 的中间过程，也有一定意义。
-
Q: Floyd 可以用来判断负环吗？
A: 可以，跑两次 Floyd，在负环上的点则 \(dis\) 一直在减少。
建图思路
- 拆点
Eg. Paired Payment
如果这里没有权值为 $(w_{a,b} +w_{b,c})^2 $ 的限制的话， 那么就可以把一个点拆成两个点（也就是两层图），然后对于每一条边也拆成两条边：\(e(u_1, v_2), e(u_2, v_1)\) 那么这样就保证了走到 \(1\) 层一定会经过两条边，所以最后答案取该层即可。对于一定要走 \(k\) 条边也可以这样处理。
但是这里有这个平方的限制。
再看一眼数据范围 \(w \le 50\)，所以可以根据这个建边了。
第 \(0\) 层为原图（不连边）， \(1 \to k\) 层表示走到这个点经过的上一条边的边权为 \(k\)，然后对于 \(u\) 以及它连接的点 \(v\) 建立 \(e({(u, 0), (v, w)}, 0)\) 然后再对于 \(u\)，枚举所有边权，建立 \(e((u, i), (v, 0), (i * w_{u, v}) ^ 2)\)，跑最短路即可。最后答案即为走到 \(s,0\) 时的权值。
Eg. 传送卷轴
这里需要处理一下传送。显然，直接连边不太现实，边数过于大了。
考虑传送的限制 \(abs(dis_x - dis_y) = k\)。
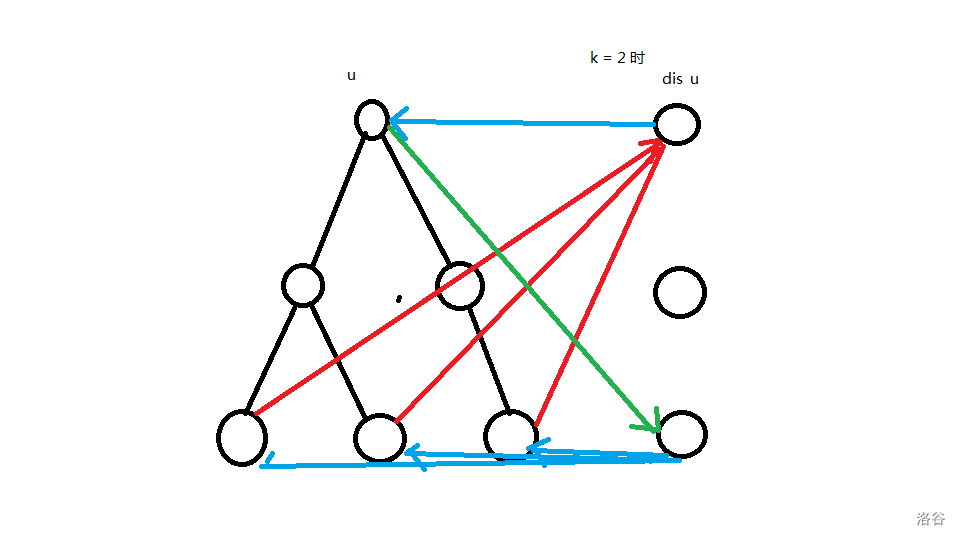
发现这里暴力连接的所有边是有重复部分的，所有同一深度的点都会指向 \(dis_i + k\) 和 \(dis_i - k\) 的所有点，考虑将重复部分不再反复建边，这时候建立 \(n\) 个中转点 \(dis_i + n\)，每次先走到 \(dis_{i \pm k}\) 这个点，然后通过这个点走到这一深度的所有点，所以只需要连接 \(u, dis_{u \pm k} +n\) 和 \(dis_i\) 到这一深度的所有点即可。
形如：
