数据结构 03栈
栈
栈模拟:
单调栈:
下面四个题是连续的,单调栈->直方图中最大的矩形->城市游戏->最大面积
描述:
给定一个长度为 N 的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出 −1。 输入格式 第一行包含整数 N,表示数列长度。 第二行包含 N 个整数,表示整数数列。 输出格式 共一行,包含 N 个整数,其中第 i 个数表示第 i 个数的左边第一个比它小的数,如果不存在则输出 −1。 数据范围 1≤N≤105 1≤数列中元素≤109 输入样例: 5 3 4 2 7 5 输出样例: -1 3 -1 2 2
代码:
//模拟栈,始终保证当前序列的单调递增
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int stk[N], tot;
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ )
{
int x; scanf("%d", &x);
while (tot >= 1 && stk[tot] >= x) tot --;
if (tot >= 1) cout << stk[tot] << " ";
else cout << "-1" << " ";
stk[++ tot] = x;
}
return 0;
}
题目:
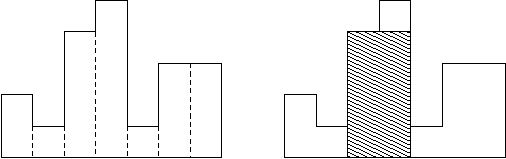
直方图是由在公共基线处对齐的一系列矩形组成的多边形。
矩形具有相等的宽度,但可以具有不同的高度。
例如,图例左侧显示了由高度为 2,1,4,5,1,3,32,1,4,5,1,3,3 的矩形组成的直方图,矩形的宽度都为 11:
通常,直方图用于表示离散分布,例如,文本中字符的频率。
现在,请你计算在公共基线处对齐的直方图中最大矩形的面积。
图例右图显示了所描绘直方图的最大对齐矩形。
输入格式
输入包含几个测试用例。
每个测试用例占据一行,用以描述一个直方图,并以整数 nn 开始,表示组成直方图的矩形数目。
然后跟随 nn 个整数 h1,…,hnh1,…,hn。
这些数字以从左到右的顺序表示直方图的各个矩形的高度。
每个矩形的宽度为 11。
同行数字用空格隔开。
当输入用例为 n=0n=0 时,结束输入,且该用例不用考虑。
输出格式
对于每一个测试用例,输出一个整数,代表指定直方图中最大矩形的区域面积。
每个数据占一行。
请注意,此矩形必须在公共基线处对齐。
数据范围
1≤n≤1000001≤n≤100000,
0≤hi≤10000000000≤hi≤1000000000输入样例:
7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0输出样例:
8 4000
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n;
int h[N];
int l[N], r[N];//分别记录左边第一个比当前高度低的下标,和当前第一个比当前高度高的下标
int q[N], tot;//单调队列【单调栈】,记录单调栈的下标
int main()
{
while (cin >> n, n)
{
for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
h[0] = h[n + 1] = -1;
//正着求一边单调上升栈,记录l,左边第一个比他小的高度
tot = 0;
q[0] = 0;
for (int i = 1; i <= n; i ++ )
{
while (tot >= 1 && h[i] <= h[q[tot]]) tot --;
l[i] = q[tot];
q[++ tot] = i;
}
//泛着求一边单调上升栈,记录r,右边第一个比他小的高度
tot = 0;
q[0] = n + 1;
for (int i = n; i >= 1; i -- )
{
while (tot >= 1 && h[i] <= h[q[tot]]) tot --;
r[i] = q[tot];
q[++ tot] = i;
}
LL ans = 0;
for (int i = 1; i <= n; i ++ )
ans = max(ans, (LL)h[i] * (r[i] - l[i] - 1));
cout << ans << "\n";
}
return 0;
}
题目:
给定一个 N×M 的 01 矩阵,矩阵下标从 0 开始。 有 Q 个询问,第 i 个询问为:将矩阵中 (xi,yi) 的元素改成 0 之后,只包含 1 的子矩阵的最大面积是多少。 注意: 每次询问均是独立的。 询问方格内元素可能本来就是 0。 子矩阵的面积是指矩阵的大小。 输入格式 第一行包含两个整数 N,M。 接下来 N 行,每行包含 M 个 01 字符。 再一行包含整数 Q。 接下来 Q 行,每行包含 2 个整数 (xi,yi)。 输出格式 每个询问输出一行一个结果,表示最大面积。 数据范围 对于 20% 的数据,1≤N,M,Q≤10 对于 50% 的数据,1≤N,M,Q≤100 对于 100% 的数据,1≤N,M≤2000,1≤Q≤105, 0≤xi<n,0≤yi<m 输入样例: 4 2 10 11 11 11 3 0 0 2 0 3 1 输出样例: 6 3 4
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int g[N][N];
int s[N][N];
int up[N][N], down[N][N];
void print(int a[N][N])
{
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ )
cout << a[i][j] << ' ';
cout << endl;
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= m; j ++ )
{
char c[2]; scanf("%s", c);
if (*c == 'F') g[i][j] = 1;
else g[i][j] = 0;
}
}
// print(g);
for (int i = 1; i <= n; i ++ )
{
int sum = 0;
for (int j = m; j >= 1; j -- )
{
if (g[i][j] == 1) sum ++;
else sum = 0;
s[i][j] = sum;
}
}
// print(s);
for (int j = 1; j <= m; j ++ )
{
get(up);
get(down)
}
return 0;
}
题目:
给定一个 N×M 的 01 矩阵,矩阵下标从 0 开始。 有 Q 个询问,第 i 个询问为:将矩阵中 (xi,yi) 的元素改成 0 之后,只包含 1 的子矩阵的最大面积是多少。 注意: 每次询问均是独立的。 询问方格内元素可能本来就是 0。 子矩阵的面积是指矩阵的大小。 输入格式 第一行包含两个整数 N,M。 接下来 N 行,每行包含 M 个 01 字符。 再一行包含整数 Q。 接下来 Q 行,每行包含 2 个整数 (xi,yi)。 输出格式 每个询问输出一行一个结果,表示最大面积。 数据范围 对于 20% 的数据,1≤N,M,Q≤10 对于 50% 的数据,1≤N,M,Q≤100 对于 100% 的数据,1≤N,M≤2000,1≤Q≤105, 0≤xi<n,0≤yi<m 输入样例: 4 2 10 11 11 11 3 0 0 2 0 3 1 输出样例: 6 3 4
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2010;
int n, m, Q;
char g[N][N];
int s[N][N];
int l[N], r[N], q[N];
int U[N], D[N], L[N], R[N];
int calc(int *h, int n)
{
h[0] = h[n + 1] = -1;
int tot = 0;
q[0] = 0;
for (int i = 1; i <= n; i ++ )
{
while (h[i] <= h[q[tot]]) tot --;
l[i] = q[tot];
q[++ tot] = i;
}
tot = 0;
q[0] = n + 1;
for (int i = n; i >= 1; i -- )
{
while (h[i] <= h[q[tot]]) tot --;
r[i] = q[tot];
q[++ tot] = i;
}
int ans = 0;
for (int i = 1; i <= n; i ++ )
ans = max(ans, h[i] * (r[i] - l[i] - 1));
return ans;
}
void init()
{
//上
memset(s, 0, sizeof s);
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ )
if (g[i][j] == '1') s[i][j] = s[i - 1][j] + 1;
else s[i][j] = 0;
U[i] = max(U[i - 1], calc(s[i], m));
}
//下
memset(s, 0, sizeof s);
for (int i = n; i >= 1; i -- )
{
for (int j = 1; j <= m; j ++ )
if (g[i][j] == '1') s[i][j] = s[i + 1][j] + 1;
else s[i][j] = 0;
D[i] = max(D[i + 1], calc(s[i], m));
}
//左
memset(s, 0, sizeof s);
for (int j = 1; j <= m; j ++ )
{
for (int i = 1; i <= n; i ++ )
if (g[i][j] == '1') s[j][i] = s[j - 1][i] + 1;
else s[j][i] = 0;
L[j] = max(L[j - 1], calc(s[j], n));
}
//右
memset(s, 0, sizeof s);
for (int j = m; j >= 1; j -- )
{
for (int i = 1; i <= n; i ++ )
if (g[i][j] == '1') s[j][i] = s[j + 1][i] + 1;
else s[j][i] = 0;
R[j] = max(R[j + 1], calc(s[j], n));
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) scanf("%s", g[i] + 1);
init();
cin >> Q;
while (Q -- )
{
int x, y; scanf("%d%d", &x, &y);
x ++, y ++;
printf("%d\n", max(max(U[x - 1], D[x + 1]), max(L[y - 1], R[y + 1])));
}
}