AcWing算法提高课【第二章搜索1】Flood Fill、最短路模型
池塘计数
链接:https://www.acwing.com/problem/content/1099/
题目:
农夫约翰有一片 N∗M 的矩形土地。 最近,由于降雨的原因,部分土地被水淹没了。 现在用一个字符矩阵来表示他的土地。 每个单元格内,如果包含雨水,则用”W”表示,如果不含雨水,则用”.”表示。 现在,约翰想知道他的土地中形成了多少片池塘。 每组相连的积水单元格集合可以看作是一片池塘。 每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。 请你输出共有多少片池塘,即矩阵中共有多少片相连的”W”块。 输入格式 第一行包含两个整数 N 和 M。 接下来 N 行,每行包含 M 个字符,字符为”W”或”.”,用以表示矩形土地的积水状况,字符之间没有空格。 输出格式 输出一个整数,表示池塘数目。 数据范围 1≤N,M≤1000 输入样例: 10 12 W........WW. .WWW.....WWW ....WW...WW. .........WW. .........W.. ..W......W.. .W.W.....WW. W.W.W.....W. .W.W......W. ..W.......W. 输出样例: 3
代码:
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 1010;
int n, m;
char g[N][N];
bool st[N][N];
int dx[8] = {-1, 0, 1, 0, -1, 1, 1, -1}, dy[8] = {0, 1, 0, -1, 1, 1, -1, -1};
void bfs(int sx, int sy)
{
queue<PII> q;
q.push({sx, sy});
st[sx][sy] = true;
while (q.size())
{
PII t = q.front();
q.pop();
for (int i = 0; i < 8; i ++ )
{
int x = t.x + dx[i], y = t.y + dy[i];
if (x < 0 || x >= n || y < 0 || y >= m) continue;
if (g[x][y] != 'W' || st[x][y]) continue;
q.push({x, y});
st[x][y] = true;
}
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ )
scanf("%s", g[i]);
int cnt = 0;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
if (!st[i][j] && g[i][j] == 'W')
{
bfs(i, j);
cnt ++;
}
printf("%d\n", cnt);
return 0;
}
题目:
1 2 3 4 5 6 7
#############################
1 # | # | # | | #
#####---#####---#---#####---#
2 # # | # # # # #
#---#####---#####---#####---#
3 # | | # # # # #
#---#########---#####---#---#
4 # # | | | | # #
#############################
(图 1)
# = Wall
| = No wall
- = No wall
方向:上北下南左西右东。
图1是一个城堡的地形图。
请你编写一个程序,计算城堡一共有多少房间,最大的房间有多大。
城堡被分割成 m∗n个方格区域,每个方格区域可以有0~4面墙。
注意:墙体厚度忽略不计。
输入格式
第一行包含两个整数 m 和 n,分别表示城堡南北方向的长度和东西方向的长度。
接下来 m 行,每行包含 n 个整数,每个整数都表示平面图对应位置的方块的墙的特征。
每个方块中墙的特征由数字 P 来描述,我们用1表示西墙,2表示北墙,4表示东墙,8表示南墙,P 为该方块包含墙的数字之和。
例如,如果一个方块的 P 为3,则 3 = 1 + 2,该方块包含西墙和北墙。
城堡的内墙被计算两次,方块(1,1)的南墙同时也是方块(2,1)的北墙。
输入的数据保证城堡至少有两个房间。
输出格式
共两行,第一行输出房间总数,第二行输出最大房间的面积(方块数)。
数据范围
1≤m,n≤50,
0≤P≤15
输入样例:
4 7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12 13
输出样例:
5
9
难度:简单
时/空限制:1s / 64MB
总通过数:2243
总尝试数:3064
来源:《信息学奥赛一本通》
算法标签
分析:
只需要注意将二进制表示的边的使用就好了
代码:
#include <cstdio>
#include <queue>
using namespace std;
const int N = 110;
typedef pair<int, int> PII;
int n, m;
int g[N][N];
int mx, sum;
bool st[N][N];
PII q[N * N];
int hh, tt;
int bfs(int sx, int sy)
{
q[0] = {sx, sy};
st[sx][sy] = true;
hh = 0, tt = 0;
int dx[4] = {0, -1, 0, 1}, dy[4] = {-1, 0, 1, 0};
int cnt = 1;
while (hh <= tt)
{
PII t = q[hh ++ ];
for (int i = 0; i < 4; i ++ )
{
int x = t.first + dx[i], y = t.second + dy[i];
if (x < 0 || x >= n || y < 0 || y >= m) continue;
if (g[t.first][t.second] >> i & 1) continue;//当前方向是墙
if (st[x][y]) continue;
cnt ++;
q[++ tt] = {x, y};
st[x][y] = true;
}
}
return cnt;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
scanf("%d", &g[i][j]);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
if (!st[i][j])
{
mx = max(mx, bfs(i, j));
sum ++;
}
printf("%d\n%d\n", sum, mx);
return 0;
}
题目:
FGD小朋友特别喜欢爬山,在爬山的时候他就在研究山峰和山谷。
为了能够对旅程有一个安排,他想知道山峰和山谷的数量。
给定一个地图,为FGD想要旅行的区域,地图被分为 n×nn×n 的网格,每个格子 (i,j)(i,j) 的高度 w(i,j)w(i,j) 是给定的。
若两个格子有公共顶点,那么它们就是相邻的格子,如与 (i,j)(i,j) 相邻的格子有(i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1),(i+1,j),(i+1,j+1)(i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1),(i+1,j),(i+1,j+1)。
我们定义一个格子的集合 SS 为山峰(山谷)当且仅当:
- SS 的所有格子都有相同的高度。
- SS 的所有格子都连通。
- 对于 ss 属于 SS,与 ss 相邻的 s′s′ 不属于 SS,都有 ws>ws′ws>ws′(山峰),或者 ws<ws′ws<ws′(山谷)。
- 如果周围不存在相邻区域,则同时将其视为山峰和山谷。
你的任务是,对于给定的地图,求出山峰和山谷的数量,如果所有格子都有相同的高度,那么整个地图即是山峰,又是山谷。
输入格式
第一行包含一个正整数 nn,表示地图的大小。
接下来一个 n×nn×n 的矩阵,表示地图上每个格子的高度 ww。
输出格式
共一行,包含两个整数,表示山峰和山谷的数量。
数据范围
1≤n≤10001≤n≤1000,
0≤w≤1090≤w≤109输入样例1:
5 8 8 8 7 7 7 7 8 8 7 7 7 7 7 7 7 8 8 7 8 7 8 8 8 8输出样例1:
2 1输入样例2:
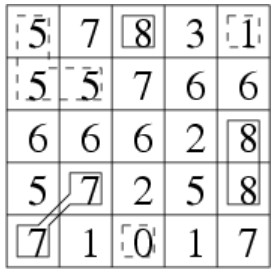
5 5 7 8 3 1 5 5 7 6 6 6 6 6 2 8 5 7 2 5 8 7 1 0 1 7输出样例2:
3 3样例解释
样例1:
样例2:
分析:
没有比当前位置更高的,那他就是最高的。
没有比当前位置更低的,那他就是最低的。
代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 1010;
int n;
int g[N][N];
bool st[N][N];
PII q[N * N];
void bfs(int sx, int sy, bool& hi, bool& lo)
{
int tt = 0, hh = 0;
q[0] = {sx, sy};
st[sx][sy] = true;
while (hh <= tt)
{
PII t = q[hh ++ ];
for (int i = -1; i <= 1; i ++ )
for (int j = -1; j <= 1; j ++ )
{
if (i == 0 && j == 0) continue;
int x = t.x + i, y = t.y + j;
// if (st[x][y]) continue;
if (x < 0 || x >= n || y < 0 || y >= n) continue;
if (g[x][y] != g[t.x][t.y])
{
if (g[x][y] > g[t.x][t.y]) hi = true;
else lo = true;
}
else if (!st[x][y])
{
q[++ tt] = {x, y};
st[x][y] = true;
}
}
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
scanf("%d", &g[i][j]);
int a = 0, b = 0;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
if (!st[i][j])
{
bool hi = 0, lo = 0;
bfs(i, j, hi, lo);
// printf("%d %d\n", hi, lo);
a += hi ? 0 : 1;
b += lo ? 0 : 1;
}
printf("%d %d\n", a, b);
return 0;
}
最短路模型
题目:
给定一个 n×nn×n 的二维数组,如下所示:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
数据保证至少存在一条从左上角走到右下角的路径。
输入格式
第一行包含整数 n。
接下来 nn 行,每行包含 nn 个整数 0 或 1,表示迷宫。
输出格式
输出从左上角到右下角的最短路线,如果答案不唯一,输出任意一条路径均可。
按顺序,每行输出一个路径中经过的单元格的坐标,左上角坐标为 (0,0),右下角坐标为 (n−1,n−1)。
数据范围
0≤n≤1000
输入样例:
5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
0 0
1 0
2 0
2 1
2 2
2 3
2 4
3 4
4 4
分析:
将st数组改为pair类型,记录每个格子从那一步回来,从终点反推。
代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 1010;
int n;
int g[N][N];
PII q[N * N];
PII pre[N][N];
void bfs(int sx, int sy)
{
memset(pre, -1, sizeof pre);
int tt = 0, hh = 0;
q[0] = {sx, sy};
pre[sx][sy] = {0, 0};
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while (hh <= tt)
{
PII t = q[hh ++ ];
for (int i = 0; i < 4; i ++ )
{
int x = t.x + dx[i], y = t.y + dy[i];
if (x < 0 || x >= n || y < 0 || y >= n) continue;
if (g[x][y]) continue;
if (pre[x][y].x != -1) continue;
pre[x][y] = {t.x, t.y};
q[++ tt] = {x, y};
}
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
scanf("%d", &g[i][j]);
bfs(n - 1, n - 1);
PII end(0, 0);
while (true)
{
printf("%d %d\n", end.x, end.y);
if (end.x == n - 1 && end.y == n - 1) break;
end = pre[end.x][end.y];
}
return 0;
}
农民 John 有很多牛,他想交易其中一头被 Don 称为 The Knight 的牛。
这头牛有一个独一无二的超能力,在农场里像 Knight 一样地跳(就是我们熟悉的象棋中马的走法)。
虽然这头神奇的牛不能跳到树上和石头上,但是它可以在牧场上随意跳,我们把牧场用一个 x,y 的坐标图来表示。
这头神奇的牛像其它牛一样喜欢吃草,给你一张地图,上面标注了 The Knight 的开始位置,树、灌木、石头以及其它障碍的位置,除此之外还有一捆草。
现在你的任务是,确定 The Knight 要想吃到草,至少需要跳多少次。
The Knight 的位置用 K 来标记,障碍的位置用 * 来标记,草的位置用 H 来标记。
这里有一个地图的例子:
11 | . . . . . . . . . .
10 | . . . . * . . . . .
9 | . . . . . . . . . .
8 | . . . * . * . . . .
7 | . . . . . . . * . .
6 | . . * . . * . . . H
5 | * . . . . . . . . .
4 | . . . * . . . * . .
3 | . K . . . . . . . .
2 | . . . * . . . . . *
1 | . . * . . . . * . .
0 ----------------------
1
0 1 2 3 4 5 6 7 8 9 0
The Knight 可以按照下图中的 A,B,C,D… 这条路径用 5 次跳到草的地方(有可能其它路线的长度也是 5):
11 | . . . . . . . . . .
10 | . . . . * . . . . .
9 | . . . . . . . . . .
8 | . . . * . * . . . .
7 | . . . . . . . * . .
6 | . . * . . * . . . F<
5 | * . B . . . . . . .
4 | . . . * C . . * E .
3 | .>A . . . . D . . .
2 | . . . * . . . . . *
1 | . . * . . . . * . .
0 ----------------------
1
0 1 2 3 4 5 6 7 8 9 0
注意: 数据保证一定有解。
输入格式
第 1 行: 两个数,表示农场的列数 C 和行数 R。
第 2..R+1 行: 每行一个由 C 个字符组成的字符串,共同描绘出牧场地图。
输出格式
一个整数,表示跳跃的最小次数。
数据范围
1≤R,C≤150
输入样例:
10 11
..........
....*.....
..........
...*.*....
.......*..
..*..*...H
*.........
...*...*..
.K........
...*.....*
..*....*..
输出样例:
5
代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 155;
int n, m;
char g[N][N];
PII q[N * N];
int d[N][N];
void bfs(int sx, int sy)
{
int tt = 0, hh = 0;
q[0] = {sx, sy};
memset(d, -1, sizeof d);
d[sx][sy] = 0;
int dx[8] = {-1, -2, -2, -1, 1, 2, 2, 1};
int dy[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
while (hh <= tt) {
PII t = q[hh ++ ];
for (int i = 0; i < 8; i ++ ) {
int x = t.x + dx[i], y = t.y + dy[i];
if (x < 0 || x >= n || y < 0 || y >= m) continue;
if (~d[x][y] || g[x][y] == '*') continue;
if (g[x][y] == 'H') {
printf("%d\n", d[t.x][t.y] + 1);
return;
}
q[++ tt ] = {x, y};
d[x][y] = d[t.x][t.y] + 1;
}
}
}
int main()
{
scanf("%d%d", &m, &n);
for (int i = 0; i < n; i ++ ) scanf("%s", g[i]);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
if (g[i][j] == 'K')
{
bfs(i, j);
// printf("%d %d\n", i, j);
}
return 0;
}
题目:
农夫知道一头牛的位置,想要抓住它。 农夫和牛都位于数轴上,农夫起始位于点 N,牛位于点 K。 农夫有两种移动方式: 从 X 移动到 X−1 或 X+1,每次移动花费一分钟 从 X 移动到 2∗X,每次移动花费一分钟 假设牛没有意识到农夫的行动,站在原地不动。 农夫最少要花多少时间才能抓住牛? 输入格式 共一行,包含两个整数N和K。 输出格式 输出一个整数,表示抓到牛所花费的最少时间。 数据范围 0≤N,K≤105 输入样例: 5 17 输出样例: 4
分析:
以前也做过这种题,什么每次加一或者乘2,当时怎么做的忘记了,但肯定不是用宽搜做的。 或许以后在遇到可以用宽搜来try一下。
代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, k;
int d[N];
int q[N];
int bfs()
{
int hh = 0, tt = 0;
q[0] = n;
memset(d, -1, sizeof d);
d[n] = 0;
while (hh <= tt)
{
int t = q[hh ++ ];
if (d[t + 1] == -1 && t + 1 <= N)
{
d[t + 1] = d[t] + 1;
q[ ++ tt] = t + 1;
}
if (d[t - 1] == -1 && t - 1 >= 0)
{
d[t - 1] = d[t] + 1;
q[++ tt] = t - 1;
}
if (d[t << 1] == -1 && (t << 1) <= N)
{
d[t * 2] = d[t] + 1;
q[++ tt] = t << 1;
}
// printf("%d %d\n", t, k);
if (t == k) return d[t];
}
return -1;
}
int main()
{
scanf("%d%d", &n, &k);
printf("%d\n", bfs());
return 0;
}