FFT&NTT数学解释
FFT和NTT真是噩梦呢
既然被FFT和NTT坑够了，坑一下其他的人也未尝不可呢
前置知识
- 多项式基础知识
- 矩阵基础知识（之后会一直用矩阵表达）
- FFT：复数基础知识
- NTT：模运算基础知识
单位根介绍
设有一个数a，使得an=1，其中n为满足an=1的最小正整数
满足条件的a有哪些呢？
- 复数域上的(cos(2π/n)+sin(2π/n)*i)（一般用ωn表示）
- 模运算中的原根g(mod n+1)
更宽泛地说，只要在一个集合中定义了加法和乘法，而且二者满足：
- 存在元素“0”，使得加上“0”的结果不变
- 存在元素“1”，使得乘以“1”的结果不变
- 加法／乘法结合律
- 加法／乘法交换律
- 乘法分配律
- 每个非0数都能做除数
- 每个数都能做加减乘数和被除数
- 加减乘除后的运算结果也在这个集合中
（这些基本上是小学学的吧，除了最后一点之外，其他都是废话）
那么里面满足an=1的数都是我们可以讨论的数
这样说，这些数也是可以满足要求的：
- 复数域上ωn的p次方
- 模运算中的原根g(mod n+1)的p次方
这里的a就是我们要找的单位根
好，这下我们来探讨一下FFT&NTT
FFT&NTT的数学推导
首先，我们要知道这两个是干什么的
FFT和NTT都是DFT的分治法下的优化
而DFT则是将多项式的系数表达（就是“满足f(x)=a+bx+cx2+dx3……的多项式”）变为点值表达（就是“经过(a,a'),(b,b'),(c,c')……的多项式”）的暴力算法
用矩阵表达就是：
很明显，DFT的时间复杂度为Θ(n2)的，这时单位元素的作用就体现出来了
我们把单位元素b及b的幂代替xi，其中b所对应的n和矩阵的边长相等，那么可以得到：
看上去就是换了个表示方法，但是变一下形就能分治了：
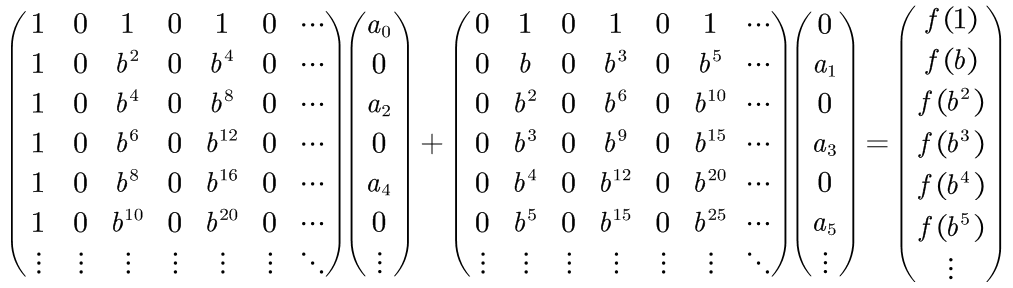
没看出来？再变一下形试试：
是不是猛然发现我们有两个相同的矩阵了？把相同的矩阵拿出来，去掉0看看：
这不就是把b2代进去的DFT式子吗，通过前面的叙述我们可以知道b2也是单位元素，那么只要一开始的n是2的幂，我们就可以分治了是不是？
事情没有这么简单，细心的可能会发现，我这里挖了一个大坑：前面那个矩阵不是一个方阵，也就是说，前面那个矩阵等于：
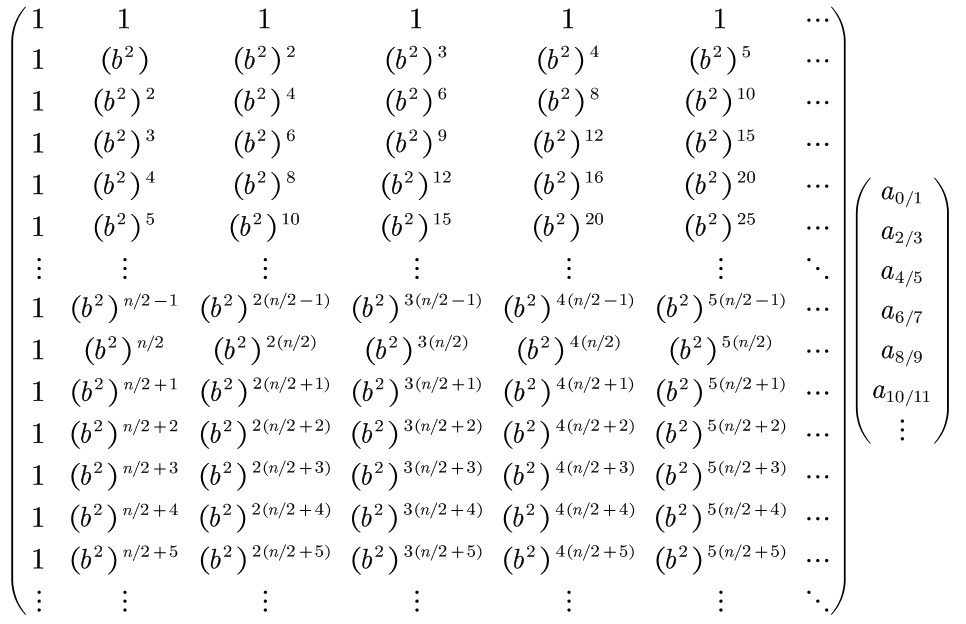
但是通过单位元素的定义可以知道，(b2)n/2=1，也就是说有：
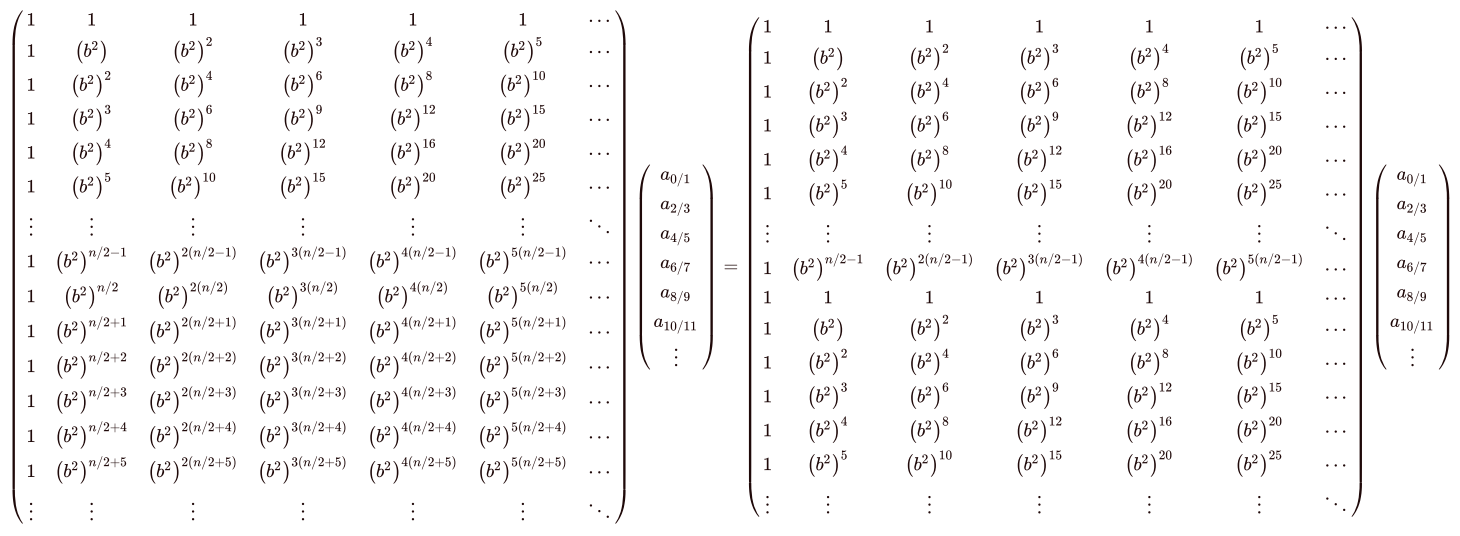
下面的半边竟然和上面的一样！忽略掉下面重复的半边矩阵，转移矩阵又变成了一个方阵，我们又可以开始分治了
知道了怎么分治计算其中一个矩阵，我们再看一下另外一个矩阵
另外一个矩阵是对角矩阵，可以在更快的Θ(n)内计算完成，但是我们想要做得更好（卡一卡常），那又怎么办呢？
这时我们可以发现，既然bn=1，n又是2的幂，那么就有bn/2=-1，也就是说：
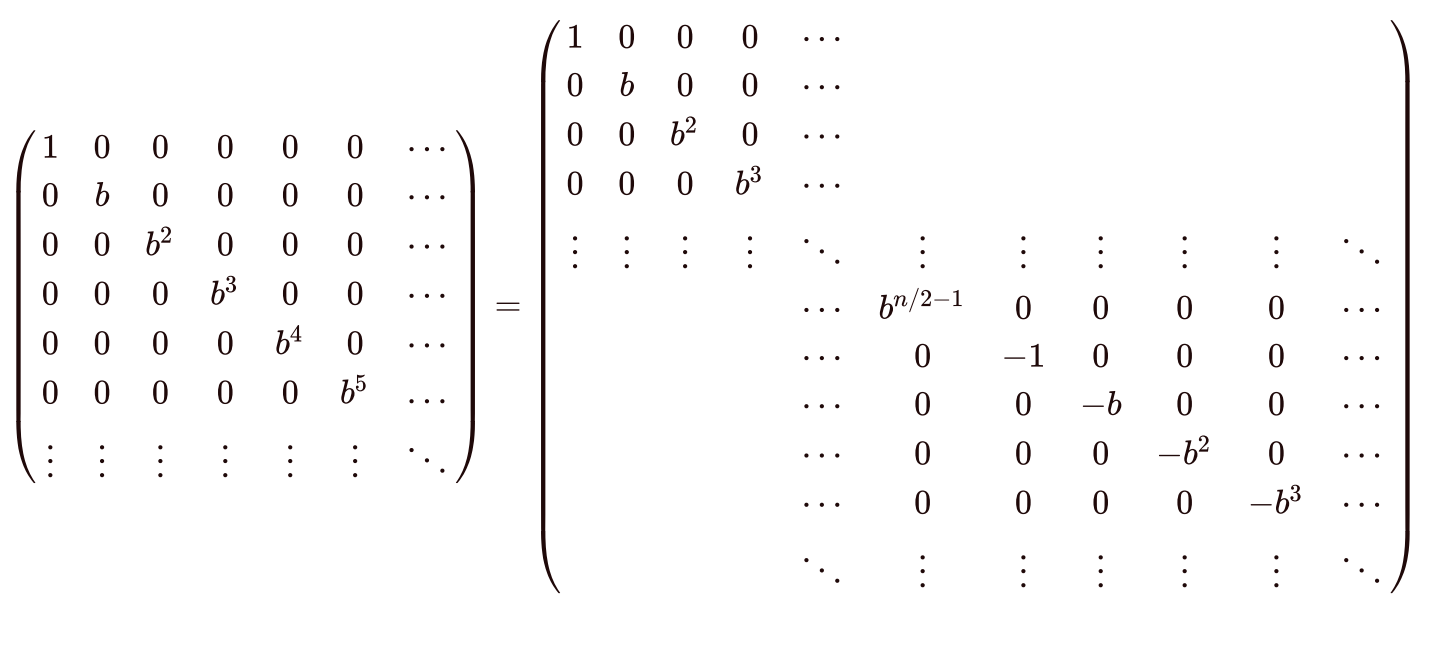
我们只要后面半边转移时用减号代替加号，而不需要再计算后面半边的幂了，常数减半
到了这一步，基本的FFT&NTT框架就到这里了
IFFT&INTT的变化
说了这么多，把系数表达变成点值表达又有什么用呢？对广大OIer来说当然是加快多项式乘法了
对系数表达式暴力相乘当然是要Θ(n2)的，但是点值表达式就只要Θ(n)了：
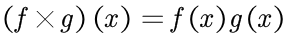
但是又怎么把点值表达变回平常的系数表达呢？这就要用到一个公式了（只要记，不用证）
这就给我们了一个IFFT&INTT的方法：把这个新的矩阵和系数再乘回去，我们熟悉的系数表达就回来了
不仅如此，既然b是单位元素，那么b-1就也是单位元素，恩……IFFT&INTT干脆就可以用FFT&NTT的代码嘛
卡常优化
DFT&IDFT的优化介绍完毕了，但是还是很慢，那有什么办法卡常呢？
递归转倍增
我们可以发现，每次分治的时候，原多项式的系数都会移动到不同的矩阵，而且系数移动和计算可以分离，可不可以先移动，再计算呢？
当然！分析之后可以发现，如果把序号为偶数的向量放在序号为奇数的向量前面，那么原来位置为p的系数会移动到rev(p)处，用图来说就是：
（用的是n=16时的例子，因为实在不好表示）
那么我们可以先移动系数，再从下向上倍增地计算，那么就能优化常数了
代码（摘自洛谷日报）：
for(int i=0;i<n;i++) r[i]=(r[i>>1]>>1)|((i&1)?n>>1:0);
多项式乘法FFT的“三次变两次”优化
当用FFT计算实系数多项式乘法时，我们可以用这样一个公式快速计算结果：
这样我们就可以把两个多项式相乘变成单个多项式的平方，因此可以偷懒少算一次FFT
参考资料
洛谷日报：https://www.luogu.org/blog/command-block/fft-xue-xi-bi-ji
PS：这里只写了其数学解释，加强理解，并不会对代码实现进行深究
2019/10/10更新
忽然发现，这个证明改一改可以变为任意长度的快速离散傅里叶变换的证明，只要把2n换成an就可以了，这样就不用做把531441=312扩充为1048576=220这种极其不划算的事了，时间复杂度和原来的应该差不多（似乎并没有什么用的样子）
——会某人
